Слайд 2Устная работа
1. Как сложить две десятичные дроби?
2. Как сложить две обыкновенные дроби?
3.

Вычислить: 4 + 1,5 =
6,3 + 3,4 =
7,2 – 4,1 =
Слайд 3Устная работа
4. Как сравнить десятичные дроби?
5. Как сравнить обыкновенные дроби, если:
а)

знаменатели равны;
б) числители равны;
в) числитель и знаменатель – разные.
6. Сравнить: 1,3 и 2,4;
3,15 и 3,17;
и ;
и ;
и .
Слайд 4Устная работа
7. Какие числа называются отрицательными?
8. Какие числа называются положительными?
9. Какие числа

называются противоположными?
10. Назовите положительные, отрицательные и противоположные числа:
-5,2; 35; 7,8; 5,2; -19; 24; -1,7; 28,6; 19; ½; -16,7; 107; 293; -½; 25,6; 15,015; -¾; 27½; -5,2; ¼; -35.
Слайд 5Когда возникли отрицательные числа? Где? Какие действия с ними умели выполнять древние?
Отрицательные

числа появились приблизительно 2100 лет тому назад в Древнем Китае.
Древние толковали о «долге» (отрицательные числа) и «имуществе» (положительные числа). Долгое время такие числа считали «несуществующими» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество – долг» приводило к недоумениям: можно сложить или вычесть «имущество» или «долги», но как понимать произведение «имущества» и «долга»? Однако несмотря на такие сомнения и недоумения действия сложения, вычитания, умножения и деления выполнялись. Правила вычисления были предложены греческим математиком Диофантом еще в
III в нашей эры.
Слайд 6Рассмотрим следующие задачи:
1. В книге доходов и расходов купца сделаны следующие записи:
Необходимо

выяснить прибыльное ли дело у купца или он имеет долг?
Решение: 1. 200 + 500 + 600 = 1300 (прибыль)
2. (-500) + (- 200) + (- 300) = -1000 (убыток)
3. 1300 + (- 1000) = 300 (прибыль)
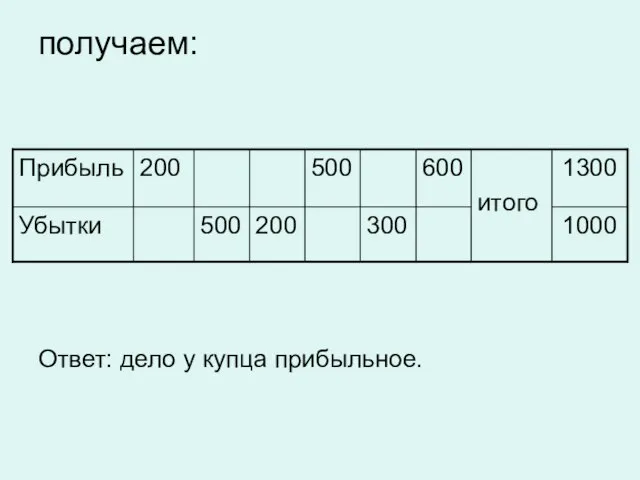
Слайд 7получаем:
Ответ: дело у купца прибыльное.
Слайд 82. Игра в кости
Надо узнать кто из участников игры выиграл, если:
- первый

игрок получил 5 штрафных и еще
7 штрафных очков;
- второй игрок получил 3 очка и 3 штрафных очков;
- третий игрок получил 4 штрафных очка и
5 очков;
- четвертый игрок получил 9 очков и
11 штрафных очков?
Слайд 9Решение:
1). -5 + (- 7) = - 12 (первый игрок)
2). 3 +

(- 3) = 0 (второй игрок)
3). (– 4) + 5 = 1 (третий игрок)
4). 9 + (- 11) = -2 (четвертый игрок)
Ответ: третий игрок выиграл.
Слайд 10Вычислить устно:
3 + (- 2) = - 5 + 4 =

- 4 + (-1) = 4,5 + (- 3) =
2 + (- 2) = 0 + (- 7) =
- 6,5 + 2 = - 8,2 + 0 =
- Какие можно сделать выводы?
Слайд 11Правила сложения чисел с разными знаками
- при сложении двух отрицательных

чисел складываем модули и перед полученным числом ставим знак «минус»;
- при сложении противоположных чисел получается нуль.
- при сложении двух чисел с разными знаками из большего модуля вычитаем меньший, и перед полученным числом, ставим знак того числа, модуль которого больше.










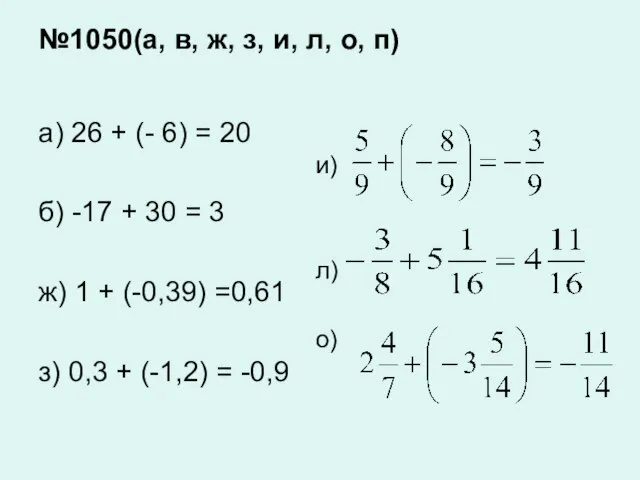


 Алгоритмическое моделирование
Алгоритмическое моделирование Военная техника Великой Отечественной войны
Военная техника Великой Отечественной войны Дети войны
Дети войны Оценочные процедуры в РСОКО. Анализ опыта Чувашской Республики.
Оценочные процедуры в РСОКО. Анализ опыта Чувашской Республики. Самостоятельная работа № 3-4 от 06
Самостоятельная работа № 3-4 от 06 швы
швы Проект «Курить – жизнь загубить!»
Проект «Курить – жизнь загубить!» Воспитательный аспект образовательного процесса
Воспитательный аспект образовательного процесса Презентация на тему Металлы и неметаллы
Презентация на тему Металлы и неметаллы Презентация на тему Химическая промышленность
Презентация на тему Химическая промышленность  Презентация на тему Кто работает ночью 1 класс
Презентация на тему Кто работает ночью 1 класс учитель английского языка МОУ Прогимназия №1 Шашкова Лилия Владимировна г. Электрогорск Ул. Советская д. 5 кв. 72. Тел. 3-47-49 2008 год
учитель английского языка МОУ Прогимназия №1 Шашкова Лилия Владимировна г. Электрогорск Ул. Советская д. 5 кв. 72. Тел. 3-47-49 2008 год ИНФОРМАЦИОННАЯ СТРАТЕГИЯ ПО ВИЧ/СПИДу В РЕСПУБЛИКЕ БЕЛАРУСЬ
ИНФОРМАЦИОННАЯ СТРАТЕГИЯ ПО ВИЧ/СПИДу В РЕСПУБЛИКЕ БЕЛАРУСЬ Многообразие насекомых, их роль в природе и жизни человека
Многообразие насекомых, их роль в природе и жизни человека Австралия и Океания.
Австралия и Океания. Виды предложений по цели высказывания и по интонации
Виды предложений по цели высказывания и по интонации Моторные расстройства при паркинсонизме и их влияние на качество жизни пациента
Моторные расстройства при паркинсонизме и их влияние на качество жизни пациента Нектар воспевания святого имени – Намамрита
Нектар воспевания святого имени – Намамрита Зачетная работа. Организационная структура отеля Крокус
Зачетная работа. Организационная структура отеля Крокус Учение Платона о государстве и праве
Учение Платона о государстве и праве Политическая сфера общества
Политическая сфера общества Времена года. Зимний лес
Времена года. Зимний лес «Снимать можно чем угодно,
«Снимать можно чем угодно, Swot-анализ
Swot-анализ К 50- летию космонавтики. Звёздное небо -это небольшая часть безграничного космоса. Земляне всех поколений всегда смотрели на него с
К 50- летию космонавтики. Звёздное небо -это небольшая часть безграничного космоса. Земляне всех поколений всегда смотрели на него с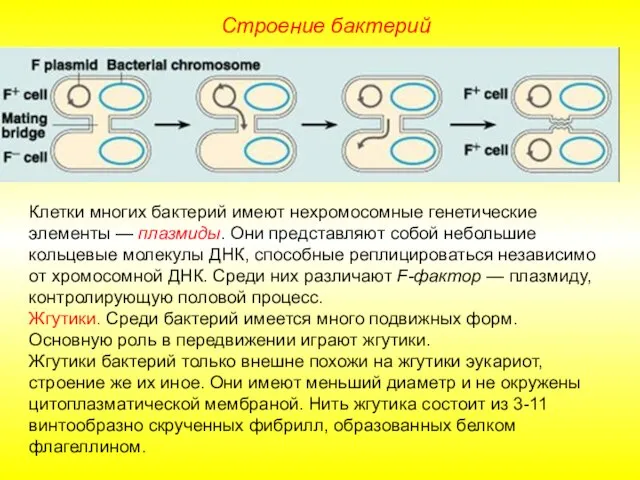 Строение бактерий
Строение бактерий Государство. понятие, признаки, сущность, социальное назначение, функции
Государство. понятие, признаки, сущность, социальное назначение, функции Шапки
Шапки