Содержание
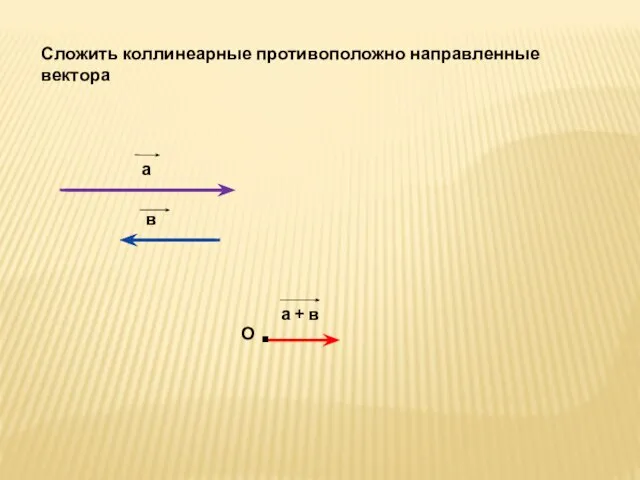
- 2. Сложить коллинеарные противоположно направленные вектора а в О а + в .
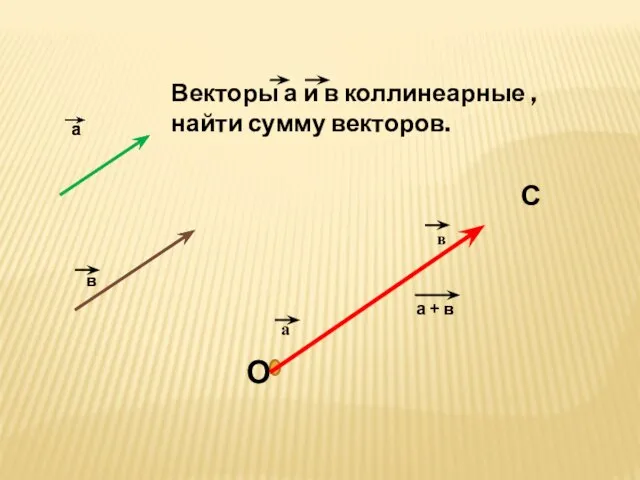
- 3. а в Векторы а и в коллинеарные , найти сумму векторов. О С а + в
- 4. От конца вектора а отложить вектор в, равный вектору в ; Провести вектор из начала вектора
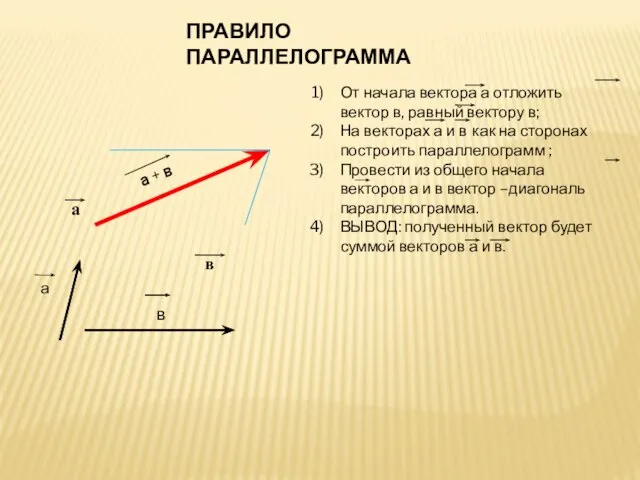
- 5. а + в ПРАВИЛО ПАРАЛЛЕЛОГРАММА От начала вектора а отложить вектор в, равный вектору в; На
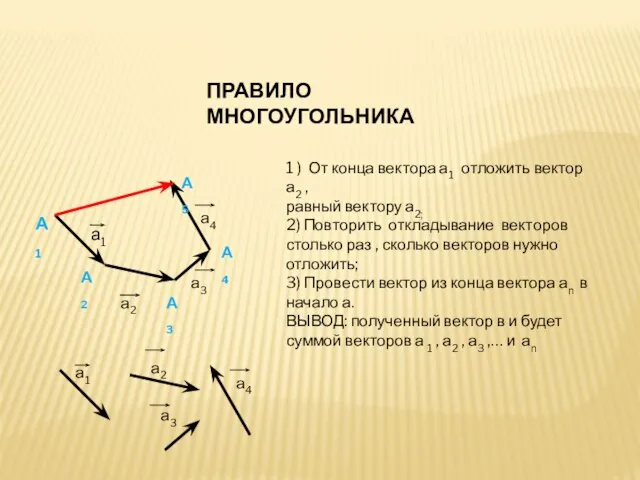
- 6. ПРАВИЛО МНОГОУГОЛЬНИКА а1 а2 а3 а4 А1 А2 А3 А4 А5 1 ) От конца вектора
- 7. ЗАКОНЫ СЛОЖЕНИЯ ВЕКТОРОВ Для любых векторов а , в и с справедливы равенства: 1) а +
- 8. ПЕРЕМЕСТИТЕЛЬНЫЙ ЗАКОН. 1.Доказательство: Рассмотрим случай ,когда векторы а и в не коллинеарны. А В а D
- 9. СОЧЕТАТЕЛЬНЫЙ ЗАКОН. Доказательство . От произвольной точки А отложим вектор АВ = а , а от
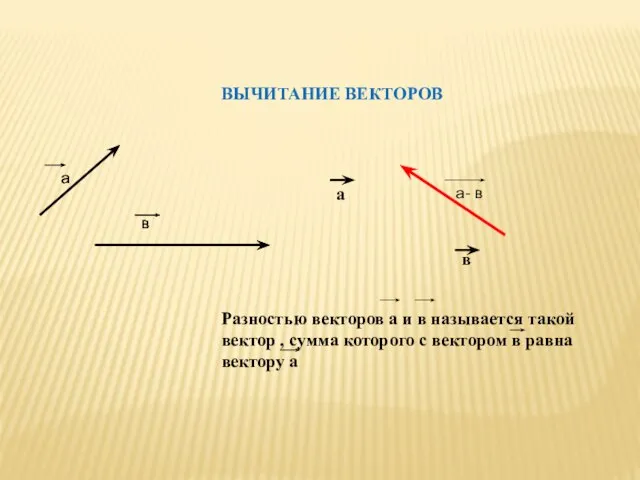
- 10. ВЫЧИТАНИЕ ВЕКТОРОВ а в а- в Разностью векторов а и в называется такой вектор , сумма
- 11. Теорема: Для любых векторов а и в справедливо равенство а – в = а +( -
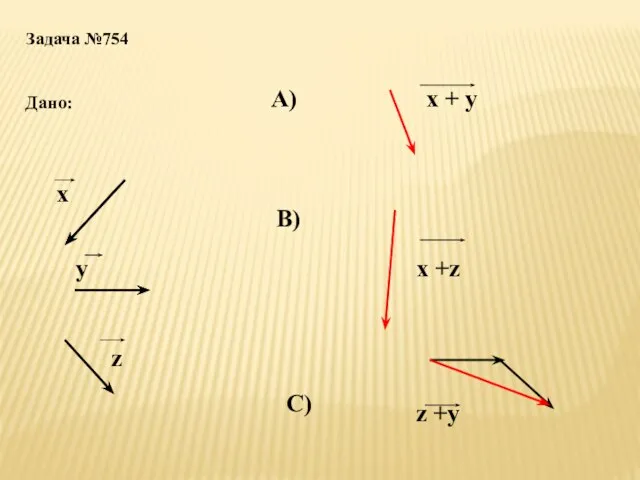
- 12. Задача №754 Дано: х у z А) х + y В) x +z C) z +y
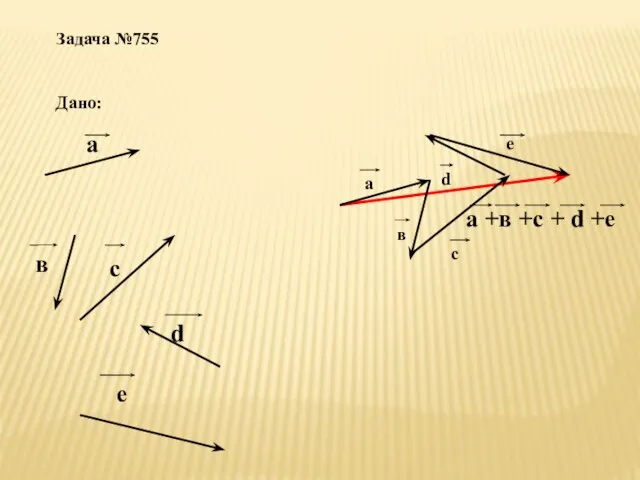
- 13. Задача №755 Дано: а в с d е а +в +с + d +е а в
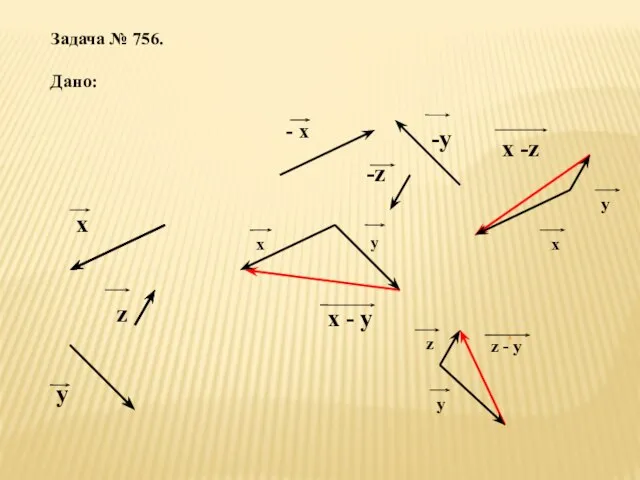
- 14. Задача № 756. Дано: х z y - х -z -y y х - у z
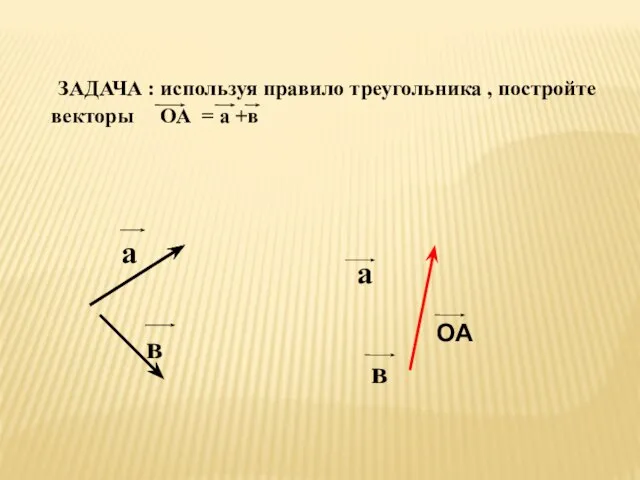
- 15. ЗАДАЧА : используя правило треугольника , постройте векторы ОА = а +в а в в ОА
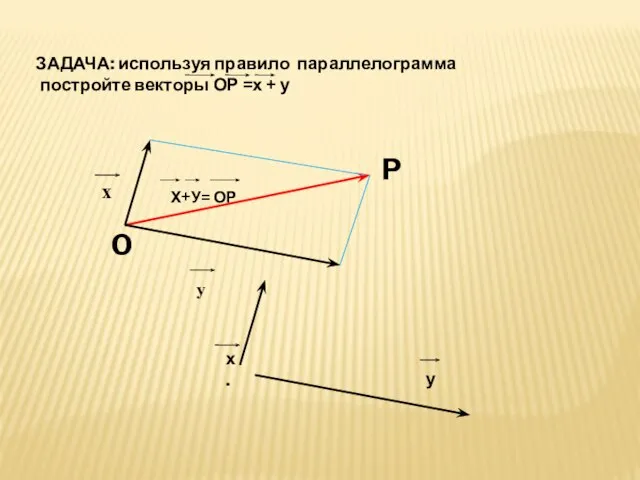
- 16. ЗАДАЧА: используя правило параллелограмма постройте векторы ОР =х + у Х+У= ОР O P х. у
- 17. Задача: Используя правило треугольника, найдите сумму векторов: а) РМ и МТ, б) СН и НС, в)
- 18. Задача : Используя правило треугольника, постройте векторы ОА = а + в и CВ = а
- 20. Скачать презентацию







 ФОЯН - Факультет ориенталистики японского напрвления
ФОЯН - Факультет ориенталистики японского напрвления Развитие игровой деятельности
Развитие игровой деятельности О взаимодействии с работодателями и потребности в специалистах, выпускаемых ИСХПР
О взаимодействии с работодателями и потребности в специалистах, выпускаемых ИСХПР Знакомим посетителей с коллективом ДОУ
Знакомим посетителей с коллективом ДОУ Управление проектами. (Лекция 4)
Управление проектами. (Лекция 4) ЗАДОРОЖНАЯ ИРИНА ВАЛЕНТИНОВНА
ЗАДОРОЖНАЯ ИРИНА ВАЛЕНТИНОВНА Carmart. Шаблон презентации
Carmart. Шаблон презентации Мысль семейная в современной женской прозе
Мысль семейная в современной женской прозе Теория решения творческих задач.Используем методы мозговой атаки, контрольных вопросов...
Теория решения творческих задач.Используем методы мозговой атаки, контрольных вопросов... LESSON STUDY Истоки
LESSON STUDY Истоки Віртуальна виставка "Сучасні заклади освіти м.Дружківка - 2014"
Віртуальна виставка "Сучасні заклади освіти м.Дружківка - 2014" Про кошек и собак 2 класс
Про кошек и собак 2 класс Профессия автомеханик
Профессия автомеханик ТК РФ как источник трудового права РФ
ТК РФ как источник трудового права РФ Амазонская низменность
Амазонская низменность Счастливая семья
Счастливая семья День России
День России День открытых дверей
День открытых дверей Искусство дарить подарки и принимать подарки
Искусство дарить подарки и принимать подарки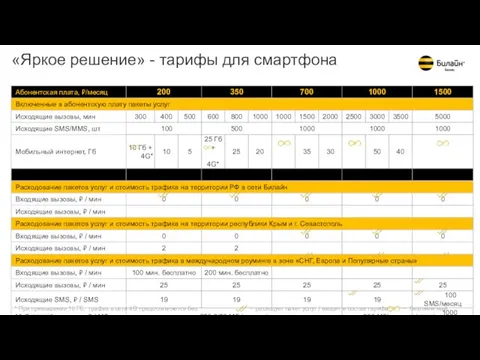 Тарифы для смартфона Яркое решение от Билайн
Тарифы для смартфона Яркое решение от Билайн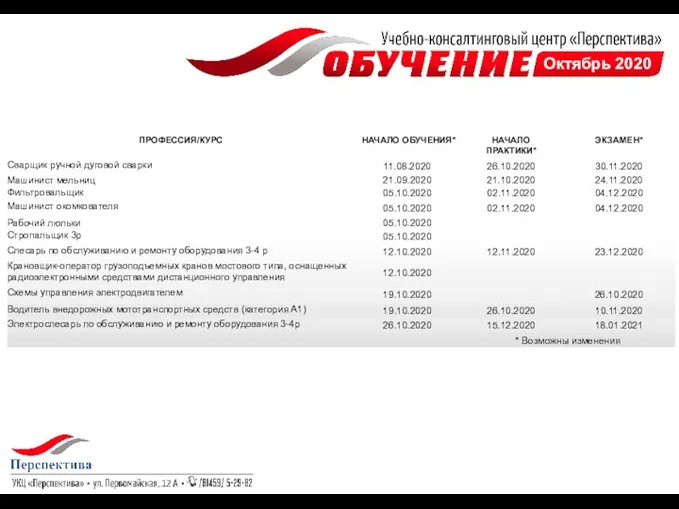 Учебно-консалтинговый центр Перспектива
Учебно-консалтинговый центр Перспектива Безопасность дорожного движения в системе образования Орловской области
Безопасность дорожного движения в системе образования Орловской области Презентация на тему Город Псков
Презентация на тему Город Псков Брянский камвольный комбинат
Брянский камвольный комбинат Композиция станковая
Композиция станковая Последние реализованные задачи и планы ЮТС по проектам
Последние реализованные задачи и планы ЮТС по проектам Презентация на тему Happy New Year (Новый год)
Презентация на тему Happy New Year (Новый год)  В. Г. Распутин «Уроки французского».
В. Г. Распутин «Уроки французского».