Содержание
- 2. Вопросы по предыдущей лекции 3) На какое время допускается обесточивание потребителей: 3 категории; 2 категории; 1
- 3. Вопросы по предыдущей лекции 4) К каким последствиям приводит нарушение электроснабжения потребителей: 3 категории; 2 категории;
- 4. Вопросы по предыдущей лекции 5) Перечислите свойства, характеризующие надежность объектов в технике. 6) Перечислите свойства, характеризующие
- 5. 1.4. События, характеризующие надежность объектов энергетики 1) Отказ работоспособности 2) Отказ функционирования 3) Авария 4) Восстановление
- 6. 1.4. События, характеризующие надежность объектов энергетики 1) Отказ работоспособности – переход объекта на более низкий уровень
- 7. 2) Отказы функционирования: Отказ срабатывания – отказ функционирования, заключающийся в невыполнении объектом требуемого срабатывания; Ложное срабатывание
- 8. События, характеризующие надежность объектов энергетики 3) Авария – переход объекта на существенно более низкий уровень работоспособности
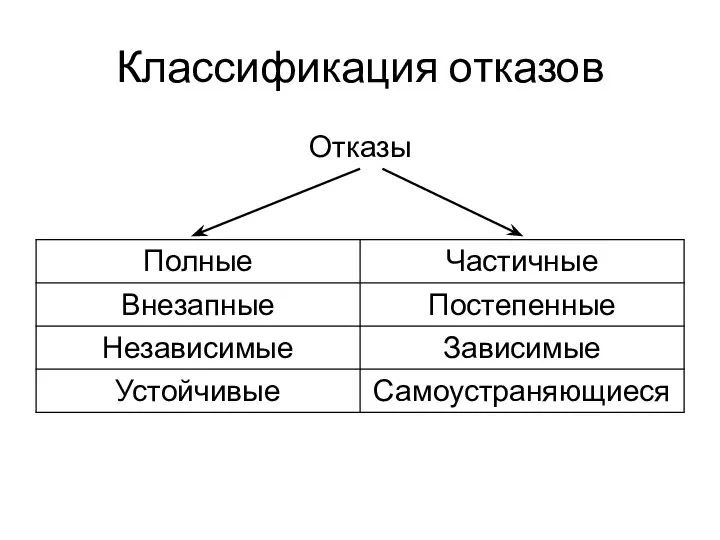
- 9. Классификация отказов Отказы
- 10. 1.5. Средства обеспечения надежности объектов энергетики Резервирование – повышение надежности объекта введением избыточности; Техническое обслуживание –
- 11. Виды резервирования Структурное Функциональное Временнόе Информационное Постоянное (неявное) Замещением (явное)
- 12. Виды резервирования Структурное – использование избыточных элементов структуры. Функциональное – использование способности элементов выполнять дополнительные функции.
- 13. Виды резервирования Информационное – использование избыточной информации. Постоянное (неявное) – когда резервный элемент предварительно нагружен, а
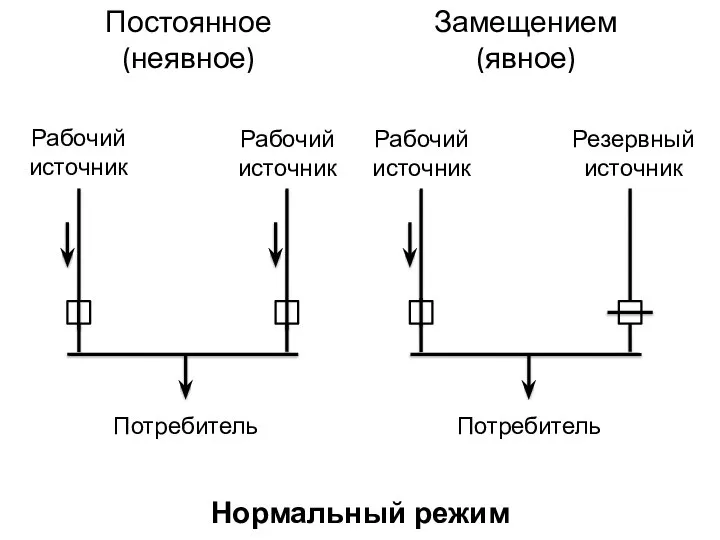
- 14. Постоянное (неявное) Рабочий источник Рабочий источник Рабочий источник Резервный источник Потребитель Потребитель Замещением (явное) Нормальный режим
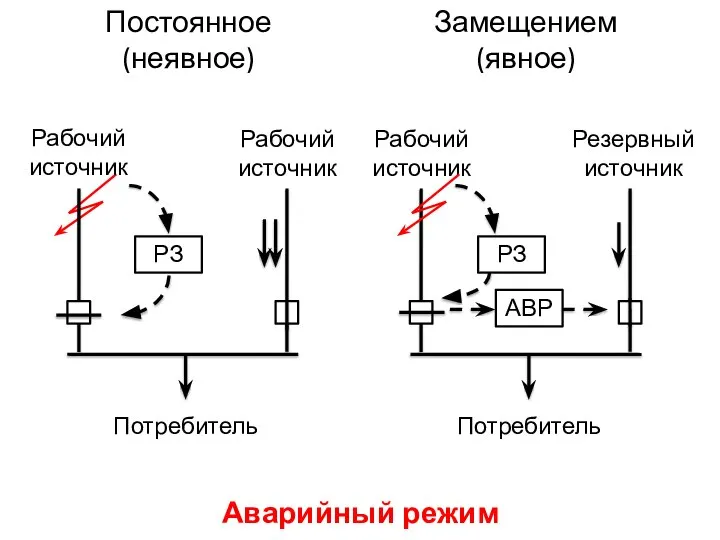
- 15. Постоянное (неявное) Замещением (явное) Аварийный режим Рабочий источник Рабочий источник Рабочий источник Резервный источник Потребитель Потребитель
- 16. Виды резервов Ремонтный – для восполнения вывода в плановый ремонт; Оперативный – для компенсации небаланса между
- 17. Баланс мощности в день максимума нагрузки в 2016 году: Руст = 238 ГВт; Ограничения: 17,1 ГВт;
- 18. Анализ видов, последствий и критичности отказов ГОСТ 27.310-95. Надежность в технике. Анализ видов, последствий и критичности
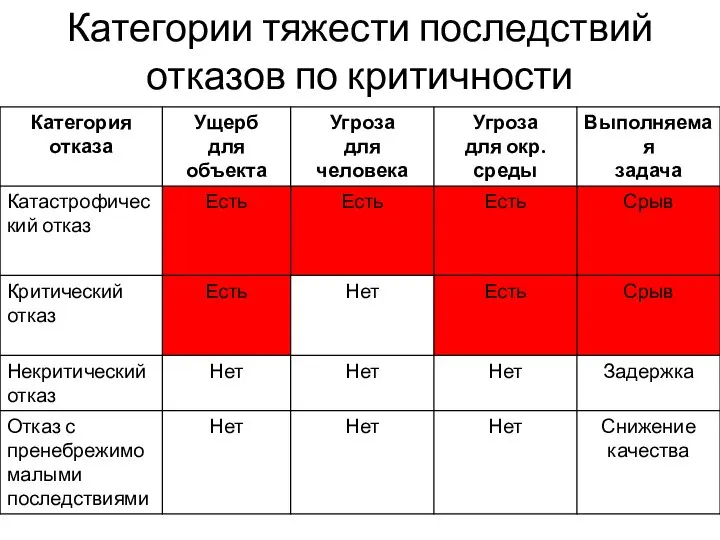
- 19. Категории тяжести последствий отказов по критичности
- 20. Категории тяжести последствий отказов по критичности
- 21. Ранги отказов по требуемой глубине анализа
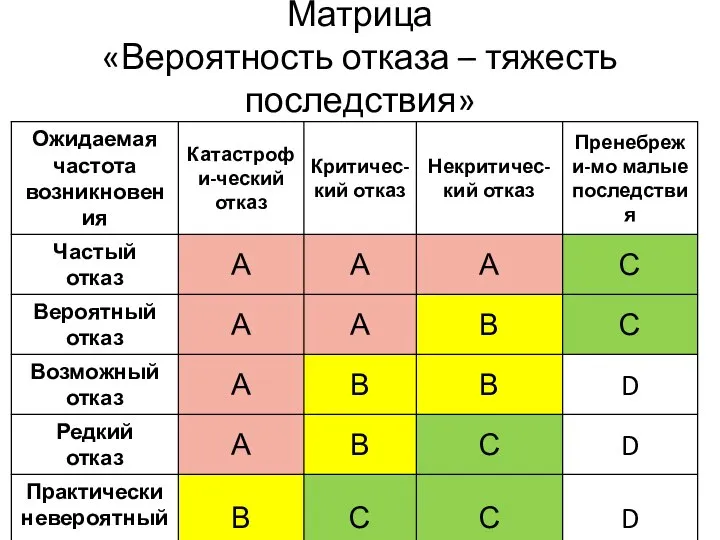
- 22. Матрица «Вероятность отказа – тяжесть последствия»
- 23. Глава 2. Элементы теории вероятности 2.1. Множества Множество – совокупность элементов А = {a1; a2; …
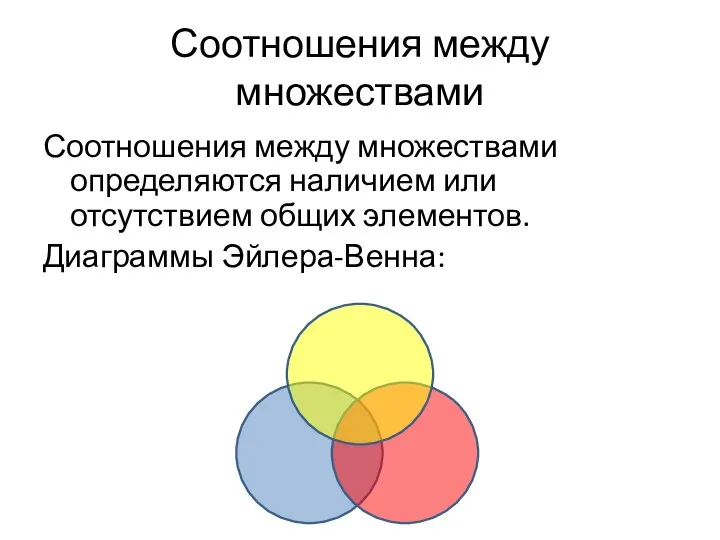
- 24. Соотношения между множествами Соотношения между множествами определяются наличием или отсутствием общих элементов. Диаграммы Эйлера-Венна:
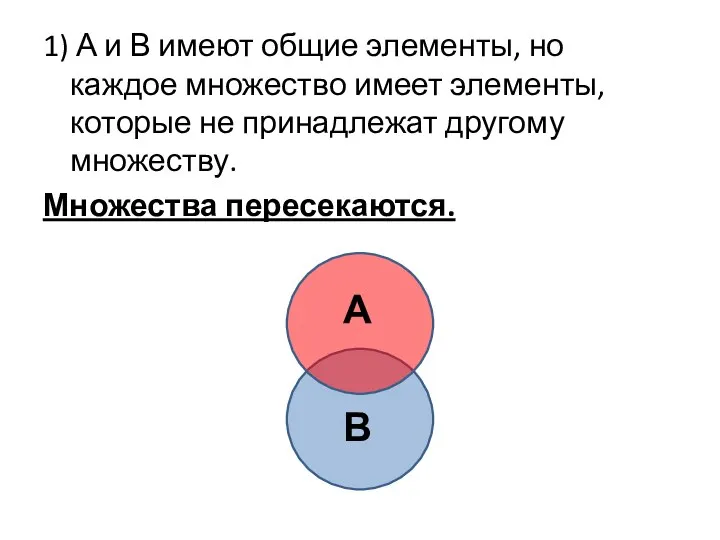
- 25. 1) А и В имеют общие элементы, но каждое множество имеет элементы, которые не принадлежат другому
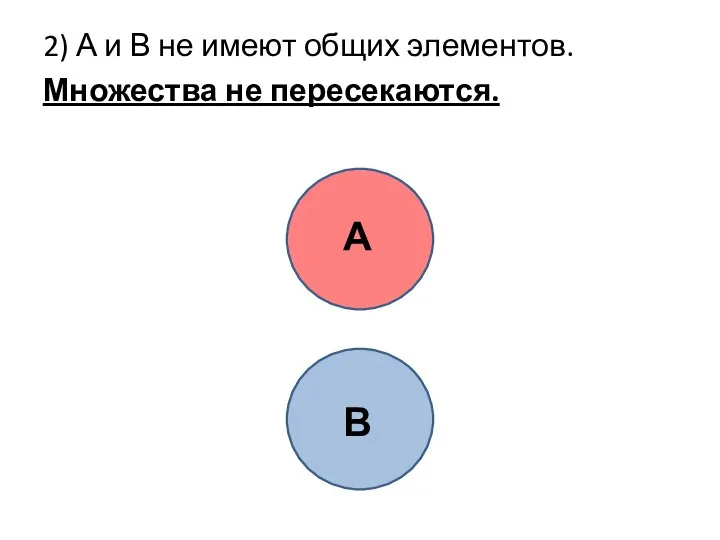
- 26. 2) А и В не имеют общих элементов. Множества не пересекаются. А В
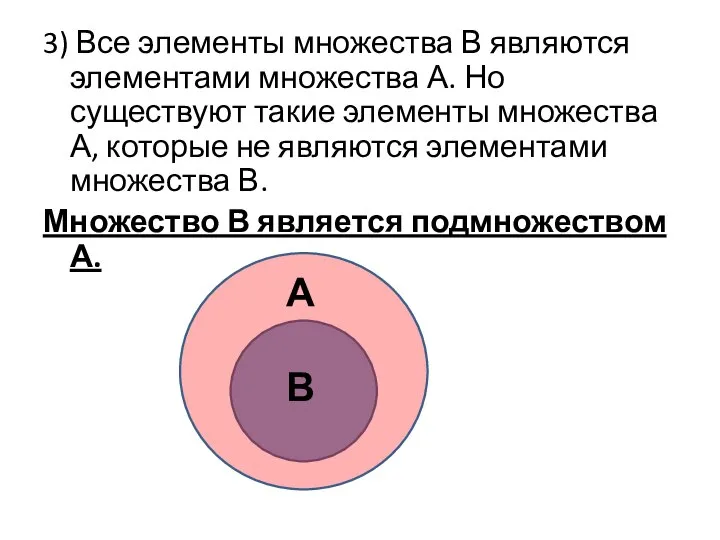
- 27. 3) Все элементы множества В являются элементами множества А. Но существуют такие элементы множества А, которые
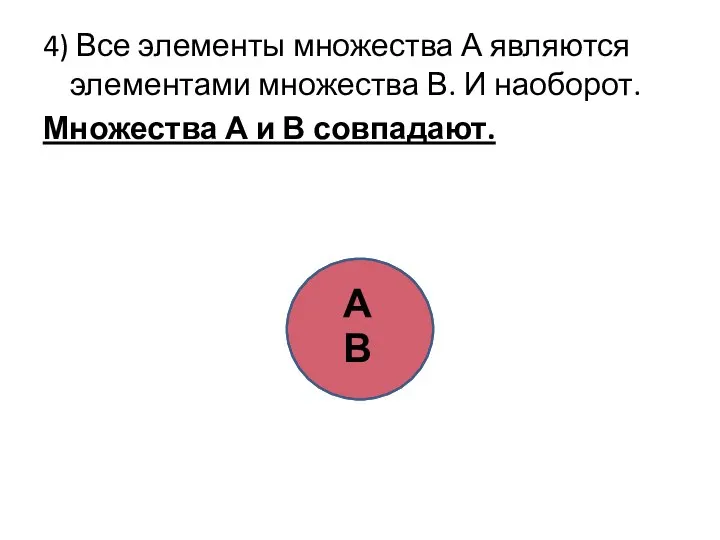
- 28. 4) Все элементы множества А являются элементами множества В. И наоборот. Множества А и В совпадают.
- 29. Операции над множествами а) Объединение б) Пересечение в) Разность г) Дополнение
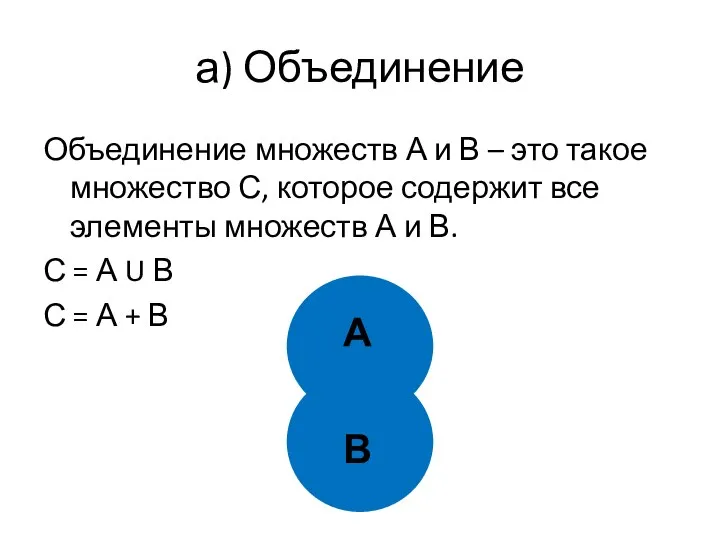
- 30. а) Объединение Объединение множеств А и В – это такое множество С, которое содержит все элементы
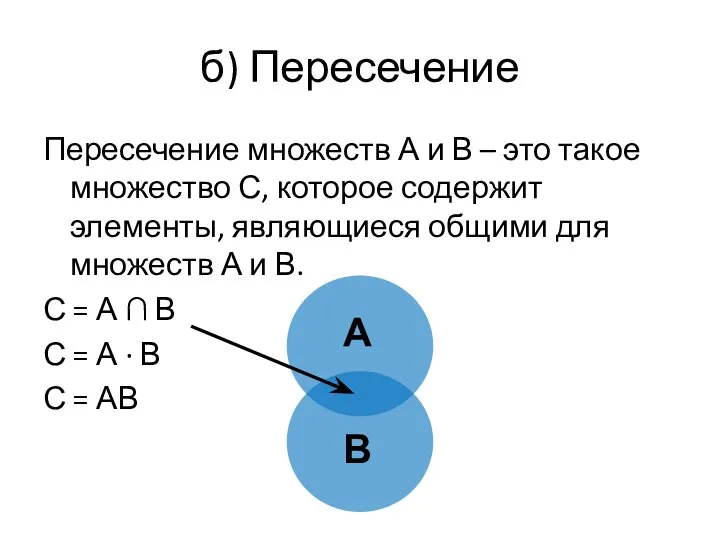
- 31. б) Пересечение Пересечение множеств А и В – это такое множество С, которое содержит элементы, являющиеся
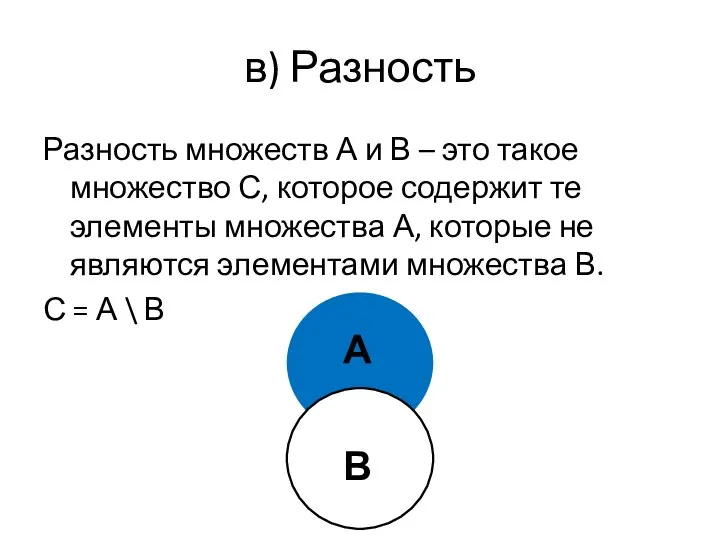
- 32. в) Разность Разность множеств А и В – это такое множество С, которое содержит те элементы
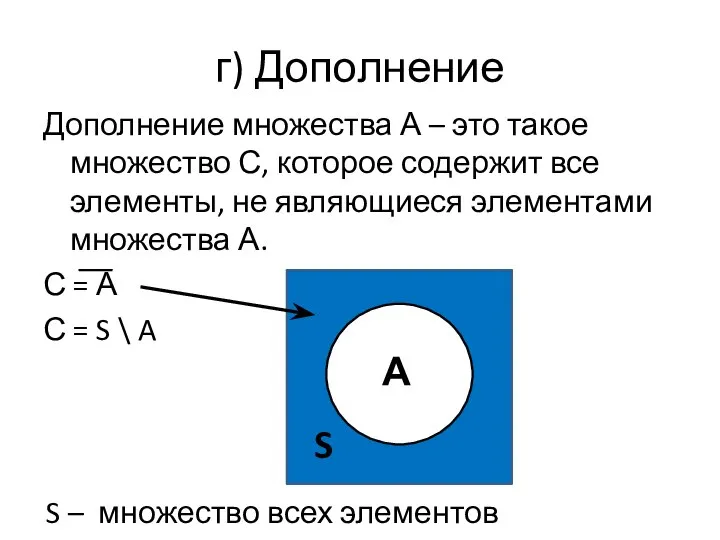
- 33. г) Дополнение Дополнение множества А – это такое множество С, которое содержит все элементы, не являющиеся
- 34. Свойства операций над множествами 1. (А + В) + В =
- 35. Свойства операций над множествами 1. (А + В) + В = A + B
- 36. Свойства операций над множествами 2. (А ∙ В) ∙ В =
- 37. Свойства операций над множествами 2. (А ∙ В) ∙ В = А ∙ В (1),(2) =>
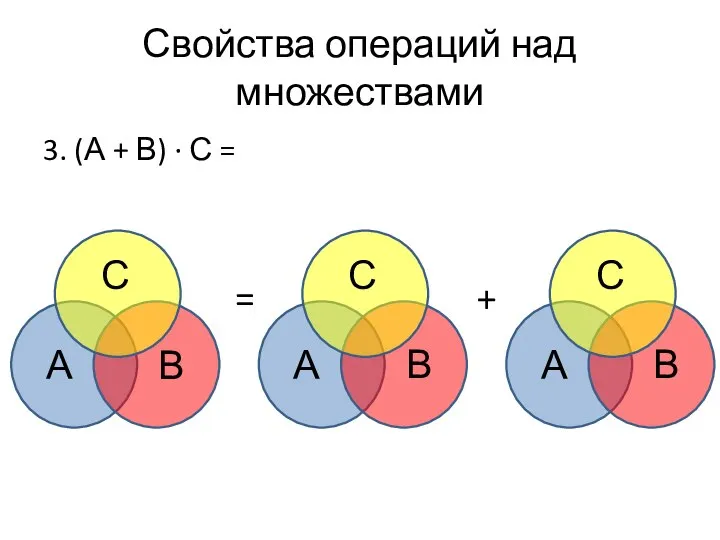
- 38. Свойства операций над множествами 3. (А + В) ∙ С = = + А В С
- 39. Свойства операций над множествами 3. (А + В) ∙ С = А ∙ С + В
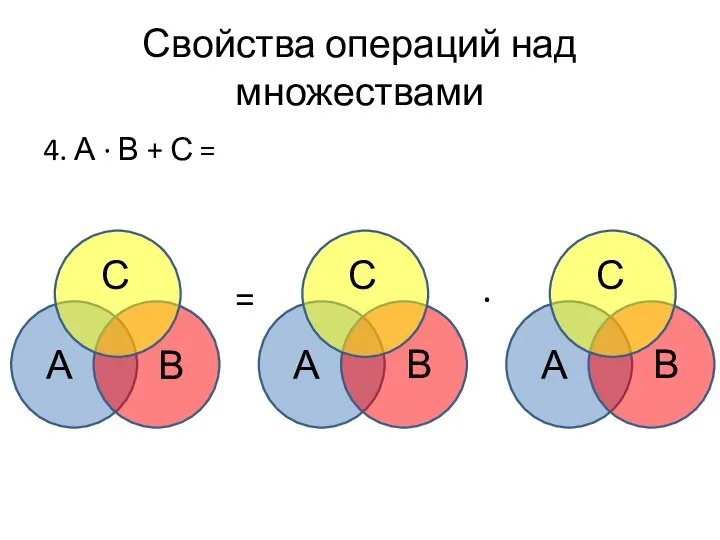
- 40. Свойства операций над множествами 4. А ∙ В + С = = ∙ А В С
- 41. Свойства операций над множествами 4. А ∙ В + С = (А + С) ∙ (В
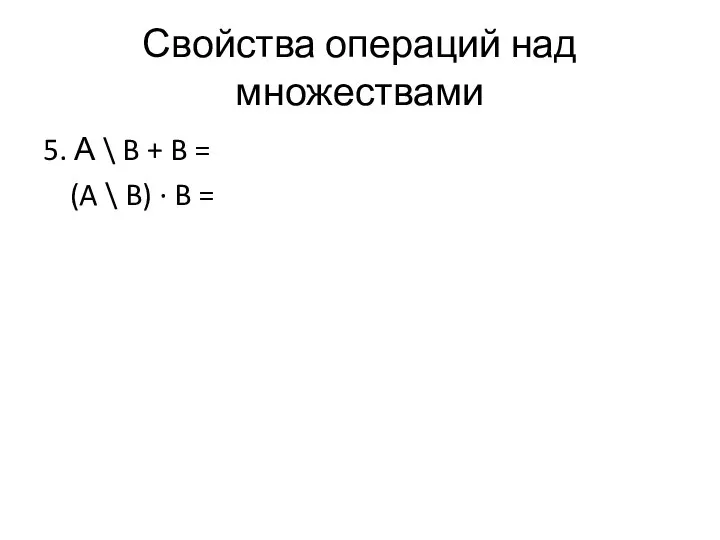
- 42. Свойства операций над множествами 5. А \ B + B = (A \ B) ∙ B
- 43. Свойства операций над множествами 5. А \ B + B = А + В (A \
- 44. Свойства операций над множествами 6. A + A = A ∙ A =
- 45. Свойства операций над множествами 6. A + A = S A ∙ A = 0
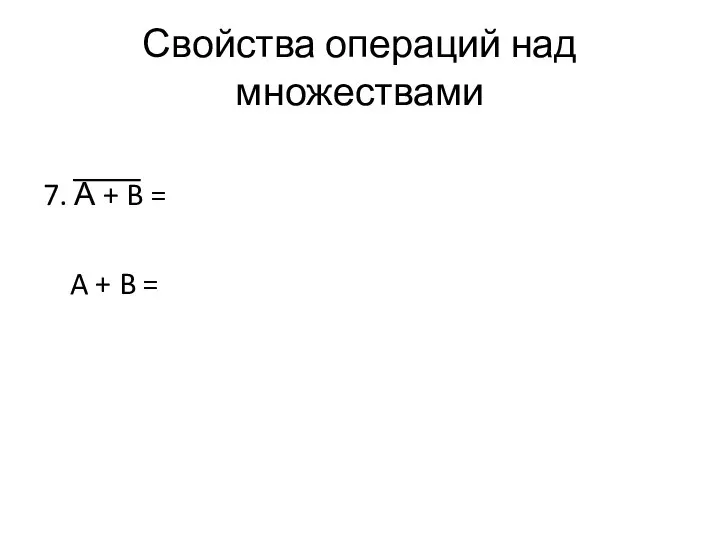
- 46. Свойства операций над множествами 7. А + B = A + B =
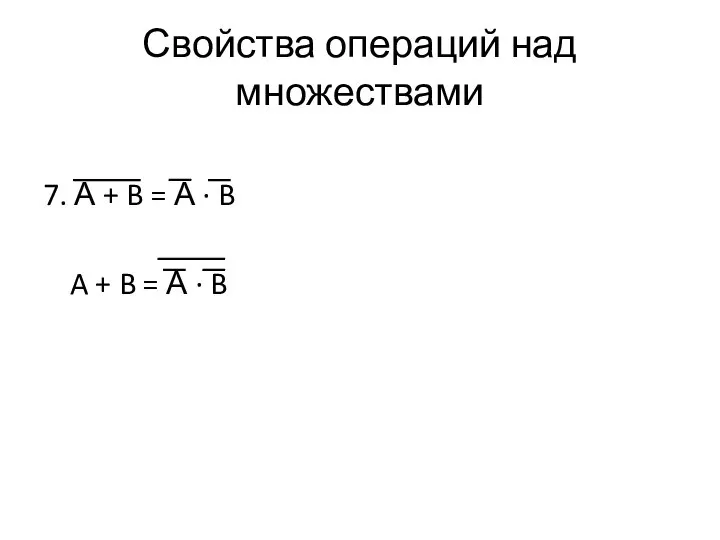
- 47. Свойства операций над множествами 7. А + B = А ∙ B A + B =
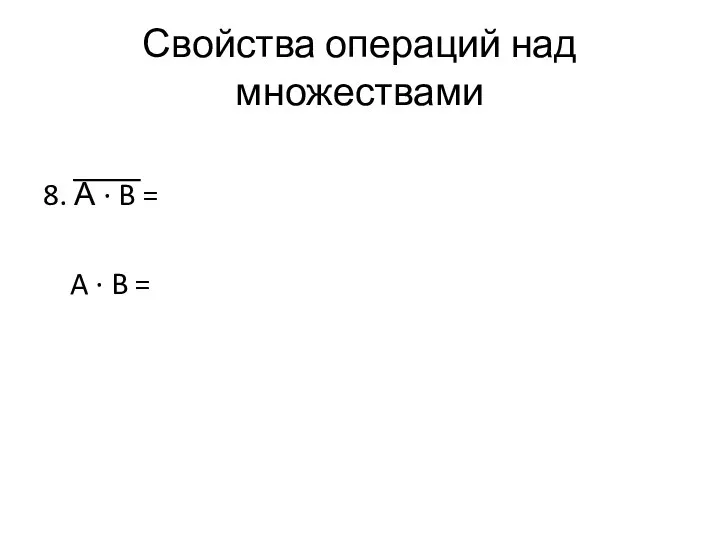
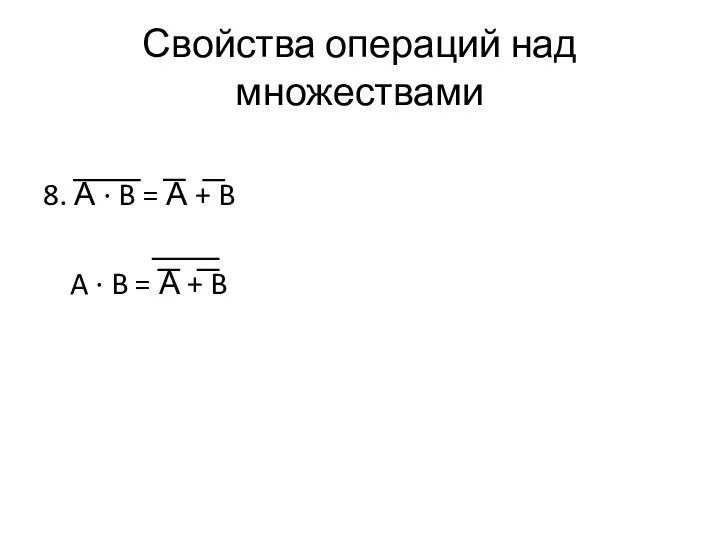
- 48. Свойства операций над множествами 8. А ∙ B = A ∙ B =
- 49. Свойства операций над множествами 8. А ∙ B = А + B A ∙ B =
- 50. 2.2. События Каждое испытание приводит к некоторому исходу. Множество всех возможных исходов – пространство элементарных событий
- 51. Пример Бросаем 2 кубика. S = {1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 2,1; …; 6,5; 6,6}
- 52. Достоверное событие – событие, которое обязательно произойдёт (U). Невозможное событие – событие, которое не может произойти
- 53. Если С1 ∙ С2 = V, то события несовместны. Если С1 ∙ С2 ≠ V, то
- 54. Полная группа событий (ПГС) ПГС – это такая группа случайных событий, что в результате опыта произойдёт
- 55. Полная группа событий (ПГС) Например, при бросании кубика обязательно произойдет одно из следующих событий: С1 –
- 56. Группа гипотез Группа гипотез – это такая ПГС, что в результате опыта произойдёт одно и только
- 57. Пример Г1 – число ≤ 2 Г2 – число ≥ 3
- 59. Скачать презентацию



































 Абсолютные и относительные величины
Абсолютные и относительные величины МЛМ — это бизнес статистики, а не убеждений
МЛМ — это бизнес статистики, а не убеждений Современные методы управления жизненным циклом самолета
Современные методы управления жизненным циклом самолета Бизнес-схемы и бизнес-процессы. Организация эффективного управления
Бизнес-схемы и бизнес-процессы. Организация эффективного управления Программа создания национального домена .РФ на основе кириллицы Андрей Колесников АНО «Координационный центр национального доме
Программа создания национального домена .РФ на основе кириллицы Андрей Колесников АНО «Координационный центр национального доме Типы химических реакций
Типы химических реакций Презентация на тему О растениях и организмов в почве
Презентация на тему О растениях и организмов в почве  Театр и музыка Древней Греции
Театр и музыка Древней Греции Алхимики
Алхимики ФИЗИОЛОГИЯ БАКТЕРИЙ
ФИЗИОЛОГИЯ БАКТЕРИЙ Медиаметрические исследования целевой аудитории для различных СМИ
Медиаметрические исследования целевой аудитории для различных СМИ ТЕХНИКА ДЛЯ ПРОИЗВОДСТВА НАТУРАЛЬНЫХ СОКОВ И НЕКТАРОВ
ТЕХНИКА ДЛЯ ПРОИЗВОДСТВА НАТУРАЛЬНЫХ СОКОВ И НЕКТАРОВ Vánoce v České republice
Vánoce v České republice Прибавление числа 2. Закрепление пройденного
Прибавление числа 2. Закрепление пройденного Бизнес от А до Я
Бизнес от А до Я Государственное общеобразовательное учреждение РК Физико-математический лицей-интернат
Государственное общеобразовательное учреждение РК Физико-математический лицей-интернат Культура общения
Культура общения Так ли обыкновенны обыкновенные дроби
Так ли обыкновенны обыкновенные дроби А.П.Чехов – несравненный художник жизни
А.П.Чехов – несравненный художник жизни Экономическое развитие. Экономическая деятельность и условия её эффективности.
Экономическое развитие. Экономическая деятельность и условия её эффективности. Маркетинговая деятельность на предприятиях
Маркетинговая деятельность на предприятиях Андрианова Наталия ВалериевнаПрезентация учителя ИЗОМОУ «Гимназия №6»г. Новочебоксарск
Андрианова Наталия ВалериевнаПрезентация учителя ИЗОМОУ «Гимназия №6»г. Новочебоксарск Взаимодействие генов. Сцепленное наследование
Взаимодействие генов. Сцепленное наследование Портрет на фоне малой Родины
Портрет на фоне малой Родины Отчет о работе Бабаевского местного отделения политической партии Единая Россия
Отчет о работе Бабаевского местного отделения политической партии Единая Россия 1000 мелочей + ElMindMap для электронного обучения Идея: Дюсьмикеев Андрей Решение: Сизонов Олег. - презентация
1000 мелочей + ElMindMap для электронного обучения Идея: Дюсьмикеев Андрей Решение: Сизонов Олег. - презентация Понятие правоотношения
Понятие правоотношения «Потенциал энергоэффективности в домашнем хозяйстве – состояние и перспективные возможности».
«Потенциал энергоэффективности в домашнем хозяйстве – состояние и перспективные возможности».