Содержание
- 2. Почему я взялась за эту работу? Я очень люблю решать задачи и разгадывать математические ребусы, но
- 3. Почему я взялась за эту работу? Поиск заключенных в софизме ошибок, ясное понимание их причин ведут
- 4. Цель и задачи. Цель: 1) Дать определение софизмам и парадоксам. 2) Определить сферу их применения. 3)
- 5. Софизм (от греч. слова, «мастерство, умение, хитрая выдумка, уловка») – это рассуждение, формально кажущееся совершенно безупречным,
- 6. В Древней Греции «софисты» (от греческого слова sofos, означающего мудрость) – мыслители, люди, авторитетные в различных
- 7. Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.
- 8. Парадокс (греч. "пара" - "против", "докса" - "мнение") близок к софизму. Но от него он отличается
- 9. Это парадоксы, которые затрагивают сферы логики и здравого смысла. Казалось бы, парадокс - и парадокс себе,
- 10. Этот древнегреческий логический парадокс имеет множество вариаций. Я приведу одну из них. Человек произносит: « Я
- 11. Чем полезны софизмы и парадоксы? Разбор софизмов и парадоксов: развивает логическое мышление, прививает навыки правильного мышления,
- 12. В своей работе я рассмотрела несколько математических софизмов и парадоксов, и сейчас приведу разбор некоторых из
- 13. Софизм №1 «Пять равно шести» Возьмем тождество 35+10-45=42+12-54. В каждой части вынесем за скобки общий множитель:
- 14. Софизм №2 «Полный стакан равен пустому» Пусть имеется стакан, наполненный водой до половины. Тогда можно сказать,
- 15. Имеется утверждение: разница между "кучей" и "не кучей" не в одном элементе. Возьмем некоторую кучу, например,
- 16. Какая линия исчезла и куда? После небольшого размышления становится ясно, что никакая отдельная линия после передвижения
- 17. Заключение Итак я познакомилась с увлекательной темой, узнала много нового, научилась решать задачки на софизмы, находить
- 19. Скачать презентацию















 Вниманию субъектов предпринимательства!
Вниманию субъектов предпринимательства! Презентация на тему Химический алфавит
Презентация на тему Химический алфавит  Аминокислоты
Аминокислоты Демографическая ситуация в Еврейской автономной области: современные тенденции и прогноз
Демографическая ситуация в Еврейской автономной области: современные тенденции и прогноз Управление затратами и контроллинг
Управление затратами и контроллинг  Основные виды обстоятельств
Основные виды обстоятельств Презентация на тему Эволюция денег Арбузова
Презентация на тему Эволюция денег Арбузова Реализм в западноевропейской живописи 19 века
Реализм в западноевропейской живописи 19 века Организация и проведение специальной оценки условий труда
Организация и проведение специальной оценки условий труда Проблемы современной педагогики и образования
Проблемы современной педагогики и образования В голубом царстве, подводном государстве
В голубом царстве, подводном государстве ПСИХИКА ЖИВОТНЫХ И ЧЕЛОВЕКА
ПСИХИКА ЖИВОТНЫХ И ЧЕЛОВЕКА 111327
111327 Афинский Акрополь
Афинский Акрополь Оригами в интерьере
Оригами в интерьере Защита прав потребителя
Защита прав потребителя «Жестокое обращение с детьми». Психологическое насилие Психологическое насилие – длительное, постоянное или периодическое возде
«Жестокое обращение с детьми». Психологическое насилие Психологическое насилие – длительное, постоянное или периодическое возде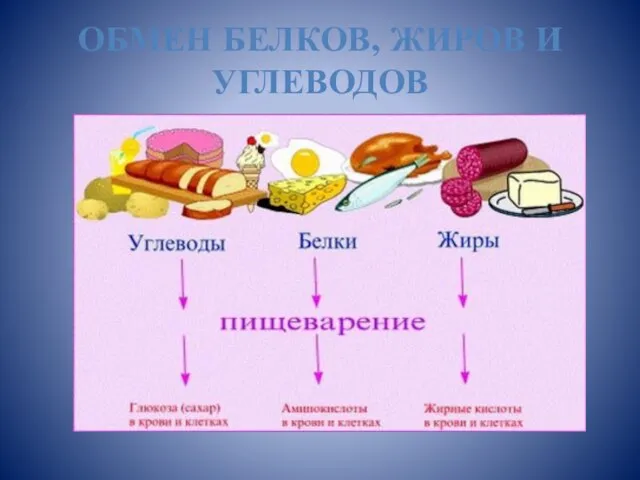 Презентация на тему Обмен белков, жиров и углеводов
Презентация на тему Обмен белков, жиров и углеводов  Беседа о толерантности
Беседа о толерантности Основное понятие происхождение: признаки, функции, формы
Основное понятие происхождение: признаки, функции, формы Русская художественная культура в первой половине 19 века
Русская художественная культура в первой половине 19 века Электронные свойства поверхности
Электронные свойства поверхности  Графическое изображение изделий из металла и искусственных материалов
Графическое изображение изделий из металла и искусственных материалов Научно-исследовательская работа СЗГМУ им. И.И. Мечникова
Научно-исследовательская работа СЗГМУ им. И.И. Мечникова Презентация на тему Методы исследования
Презентация на тему Методы исследования Военная форма ВС РФ
Военная форма ВС РФ Презентация на тему Достопримечательности Ставрополя
Презентация на тему Достопримечательности Ставрополя Межличностные конфликты, их конструктивное разрешение
Межличностные конфликты, их конструктивное разрешение