Теория Информации

Mathematical Backgrounds.
Information Theory
In 1949, Shannon provides a theoretical foundations for cryptography based on his fundamental work on information theory. He measured the theoretical secrecy of a cipher by the uncertainty about the plaintext given the received ciphertext. If, no matter how much ciphertext is intercepted, nothing can be learned about the plaintext, the cipher achieves perfect secrecy.
Entropy and Equivocation
Information theory measures the amount of information in a message by the average number of bits needed to encoded all possible messages in an optimal encoding. The Sex field in a database, for example, contains only one bit of information because it can be encoded with one bit (Male can be represented by “0”, Female by “1”). If the field is represented by an ASCII character encoding of the character strings “MALE” and “FEMALE”, it will take up more space, but will not contain any more information.

Mathematical Backgrounds.
Information Theory
The amount of information in a message is formally measured by the entropy of the message. The entropy is a function of the probability distribution over the set of all possible messages. Let X1,..., Xn be n possible messages occurring with probabilities p(X1),...,p(Xn), the sum of this probabilities p(Xi), i=1,...,n equals to one. The entropy of a given message is defined by the weighted average:
H(X)=−Σinp(Xi)log2 p(Xi).
As the sum taken over all messages X:
H(X)=–ΣXp(X)log2 p(X)=ΣXp(X)log2 [1/p(X)].

Mathematical Backgrounds.
Information theory in Examples
Intuitively, each term log2 [1/p(X)] in last expression represents the number of bits needed to encode message X in an optimal encoding that is, one which minimizes the expected number of bits transmitted over the channel. The weighted average H(X) gives the expected number of bits in optimally encoded messages.
Because 1/p(X) decrease as p(X) increase, an optimal encoding uses short codes for frequently occurring messages at the expense of using longer ones for infrequently messages. This principle is applied in Morse code, where the most frequently used letters are assigned the shortest codes.
“Huffmen Code” are optimal codes assigned to characters, words, machine instructions, or phases. Single – character Huffmen code are frequently used to compact large files. COMPACT program on UNIX reduced its storage requirements by 38%, which is typical for text files.

Mathematical Backgrounds.
Information theory in Examples
Example. Let n=3, and let the 3 messages be the letters A,B, and C, where p(A)=1/2 and p(B)=p(C)=1/4. Then
log2(1/ p(A))=log22= 1;
log2(1/ p(B))=log2(1/p(C))=log24=2;
what confirming our earlier observation, that for frequently occurring message the minimal number of bits is needed for optimal encoding.
Example. Suppose there are two possibilities: Mail and Female, both equally likely; thus p(Male)=p(Female)=1/2. Then
H(X)=p(Male)log2(1/ p(Male))+p(Female)log2(1/ p(Female))=
=(1/2)(log22)+(1/2)(log22)= 1,
what confirming our earlier observation that there is 1 bit of information in the Sex field of a database.
The following example illustrate the application of entropy to determine the information content of a massage.

Example. Let n=3, and let the 3 messages be the letter A,B,and C, where p(A)=1/2, p(B)=p(C)=1/4. Then
H(X)=(1/2)log22+2(1/4)log24=0.5+1.0=1.5.
An optimal encoding assigns a 1-bit code to A and 2-bit codes to B and C. For example, A can encoded with the bit 0, while B and C can be encoded with two bits each, 10 and 11. Using this encoding, the 8-letter sequence ABCAABAC is encoded as the 12-bit sequence 010110010011 as shown next:
A B C A A B A C
0 10 11 0 0 10 0 11
The average number of bits per letter is 12/8=1,5.
Mathematical Backgrounds.
Information theory in Examples

Mathematical Backgrounds
Information theory in Examples
For a given language, consider the set of all messages N character long. The rate of the language for messages of length N is defined by
r=H(X)/N,
That is, the average number of bits of information in each character.
The simplest solution to determine the rate of language (absolute rate R) based on the assumption that all letters have the same probability of occurring within the all possible messages, as well as all possible sequences of characters are equally likely. If there are L characters in the language, then the absolute rate is given by
R=log2L,
For English language this probability is equal to L=1/26, then R=log2L=log226 =4,7bit/letter.
The absolute rate of the language is defined to be the maximum number of bits of information that could be encoded in each character.
The actual rate of English is thus considerably less than its absolute rate. The reason is that English, like all natural languages, is highly redundant. For example, the phrase “occurring frequently” could be reduced by 58% to “crng frg” without loss of information.

Mathematical Backgrounds
Information theory in Examples
1.Single letter frequency distributions.
Then r=H(1-grams)/1=4.15.
2.Diagrams frequency distributions. Certain diagrams (pair of letters) such as TH and EN occur much more frequently than others. Some diagrams (e.g., OZ) never occur in meaningful messages (acronyms are on exception). Then r=H(2-grams)/2=3.62.
3.Trigrams frequency distributions. The proportion of meaningful sequences decreases when trigrams are considered (e.g. BB is meaningful but BBB is not). Such as THE and ING occur much more frequently than others. Then r=H(3-grams)/2=3.22.

The rate of a language (entropy per character) is determined by estimating the entropy of N-grams for increasing values of N. As N increases, the entropy per character decreases because there are fewer choices and certain choices are much more likely. For N→∞ ,r=1÷1,5.
The redundancy of a language with rate r and absolute rate R is defined by D=R−r. For R=4.7 and rate r=1, D=3.7, whence the ratio D/R shows English to be about 79% redundant; for r=1.5, D=3.2, implying a redundancy of 68%.
Mathematical Backgrounds
Information theory in Examples

Mathematical Backgrounds Perfect Secrecy
Shannon studied the information theoretic properties of cryptographic systems in terms of three classes of information:
1.Plaintext messages M occurring with prior probabilities p(M), where ΣMp(M)=1.
2.Ciphertext messages C occurring with prior probabilities p(C), where ΣCp(C)=1.
3.Keys K occurring with prior probabilities p(K), where ΣKp(K)=1.
Let pc(M) be the probability that message M was sent given that C was received (thus C is the encryption of message M). Perfect secrecy is defined by the condition.
pC(M)=p(M)
That is, intercepting the ciphertext gives a cryptanalyst no additional information.

Mathematical Backgrounds Perfect Secrecy
A necessary and sufficient condition for perfect secrecy is that for every C,
pM(C)=p(C) for all M,
This means the probability of receiving a particular ciphertext C given that M was sent (enciphered under the same key) is the same as the probability of receiving C given that some other message M’ was sent (enciphered under a different key).
Perfect secrecy is possible using completely random keys at least as long as the messages they encipher.

Mathematical Backgrounds Perfect Secrecy
Next figure illustrates a perfect secrecy system with four messages, all equally likely, and four keys, also equally likely.
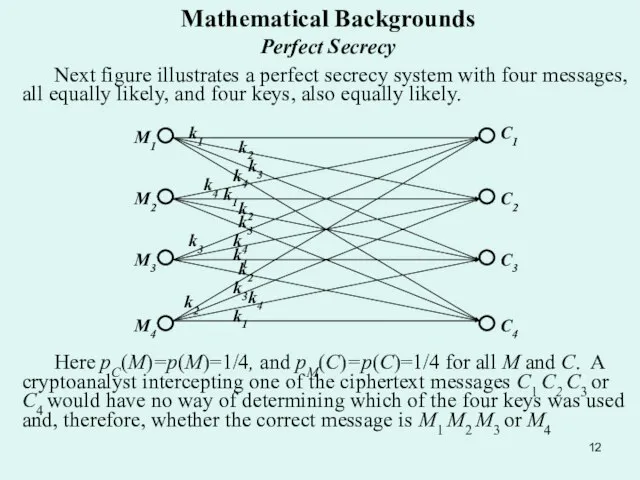
Here pC(M)=p(M)=1/4, and pM(C)=p(C)=1/4 for all M and C. A cryptoanalyst intercepting one of the ciphertext messages C1 C2 C3 or C4 would have no way of determining which of the four keys was used and, therefore, whether the correct message is M1 M2 M3 or M4

Mathematical Backgrounds Perfect Secrecy
Perfect secrecy requires that the number of keys must be at least as great as the number of possible messages. Otherwise there would be some message M such that for given C, no K decipher C into M, implying pC(M)=0. The cryptanalyst could thereby eliminate certain possible plaintext message from consideration, increasing the chances of breaking the cipher.
A cipher using a nonrepeating random key stream such as the one described in the preceding example is called a one-time pad.One-time pads are the only ciphers that achieve perfect secrecy.
The implementation of one-time pads in computer systems is based on an ingenious device designed by Gilbert Verman in 1917. Letting M=m1m2... denotes a plaintext bit stream and K=k1k2... a key bit stream, the Verman cipher generates a ciphertext bit stream C=EK(M)=c1c2... , where ci=(mi+ki) mod 2, i=1,2,... . The Verman cipher is efficiently implemented in microelectronics by taking the “exclusive-or” of each plaintext/key pair ci=mi+ki Because ki+ki =0 for ki=0 or 1, deciphering is performed with the same operation: ci+ki = mi+ki+ki=mi .

Mathematical Backgrounds Perfect Secrecy
Example M=0111001101010101, K=0101011100101011, here the key stream represent the stream of random bits with probabilities p(0)=p(1)=0.5.
Enciphering procedure: C=M⊕K=0111001101010101⊕ ⊕ 0101011100101011=0010010001111110.
Deciphering procedure: M=C⊕K=0010010001111110⊕ ⊕ 0101011100101011= 0111001101010101.

Mathematical Backgrounds Complexity Theory
The strength of a cipher is determined by the computational complexity of the algorithms used to solve the cipher. The computational complexity of an algorithm is measured by its time T and space S requirements are expressed as function f(n) of n, and n characterized the size of the input. This function is typically bounded as an “order-of-magnitude” of the form O(nt), where t can take any constant value.
For example if f(n) is a polynomial of the form f(n)=atnt+
at-1 nt-1 +…+a1n1 +a0 for constant t, then f(n)=O(nt); that is, all constants and low-order terms are ignored.
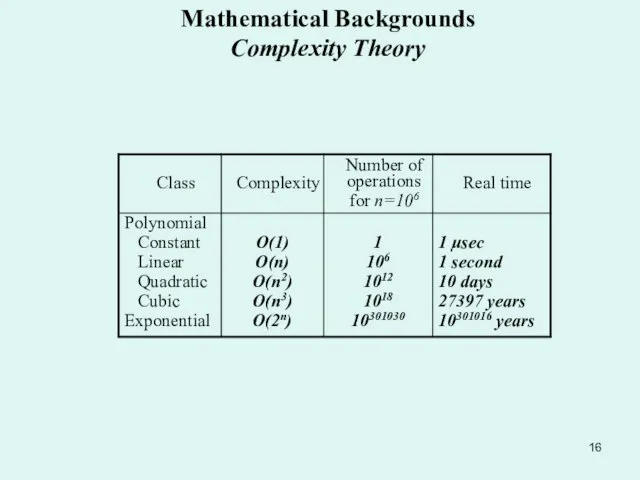
Measuring the time and space requirements of an algorithm by its order-of-magnitude allows to see how the time and space requirements grows as the size of the input increases. For example, if T=O(n2), doubling the size of the input quadruples the running time. Table 2.4.1 shows the running times of different classes of algorithms for n=106.

Mathematical Backgrounds Complexity Theory

Mathematical Backgrounds Complexity Theory
Complexity theory classifies a problem according to the minimum time and space needed to solve the hardest instances of the problem based on some abstract model of computation.
The class P consists of all problems solvable in polynomial time.
The class NP (nondeterministic polynomial) consists of all problems solvable in polynomial time on nondeterministic model of computation.
The class NP-complete has the property that if any one of the problems is in P, then all NP problems are in P and P=NP. Thus the NP-complete problems are the “hardest” problem in NP. The fastest known algorithms for systematically solving these problems have worst-case time complexities exponential in the size n of the problem.