Содержание
- 2. ОПРЕДЕЛЕНИЕ СПЕКТРА СИГНАЛА Спектр сигнала (спектральный образ сигнала) – коэффициенты разложения сигнала в некотором базисе ортогональных
- 3. ОСНОВНЫЕ СПЕКТРАЛЬНЫЕ ТЕОРЕМЫ 2 Свойство линейности – спектр суммы равен сумме спектров. Теорема запаздывания Теорема Парсеваля-Релея
- 4. СПЕКТР ОДИНОЧНОГО ПРЯМОУГОЛЬНОГО ИМПУЛЬСА 3 Пусть имеется одиночный прямоугольный импульс амплитудой E, и длительностью τ.
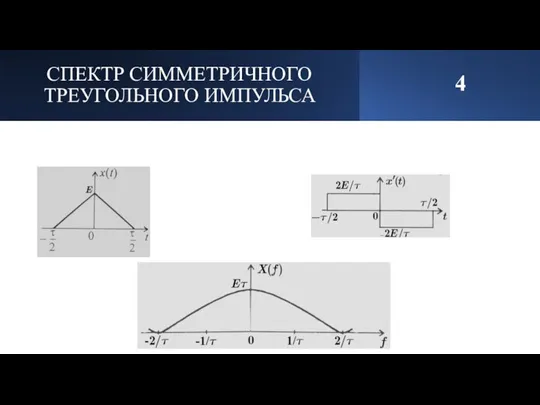
- 5. СПЕКТР СИММЕТРИЧНОГО ТРЕУГОЛЬНОГО ИМПУЛЬСА 4
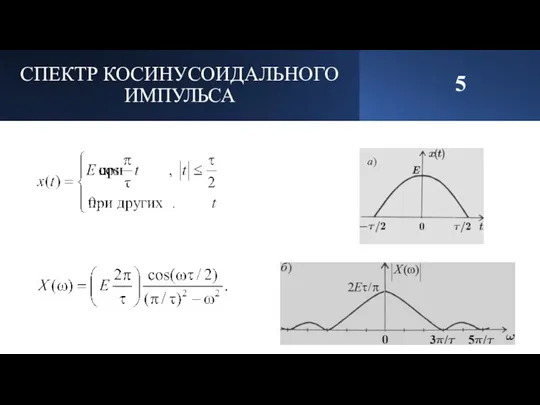
- 6. СПЕКТР КОСИНУСОИДАЛЬНОГО ИМПУЛЬСА 5
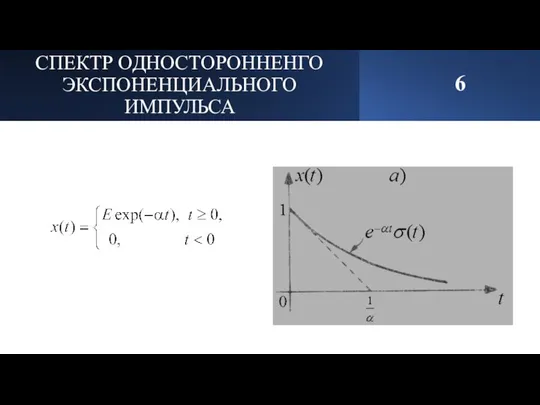
- 7. СПЕКТР ОДНОСТОРОННЕНГО ЭКСПОНЕНЦИАЛЬНОГО ИМПУЛЬСА 6
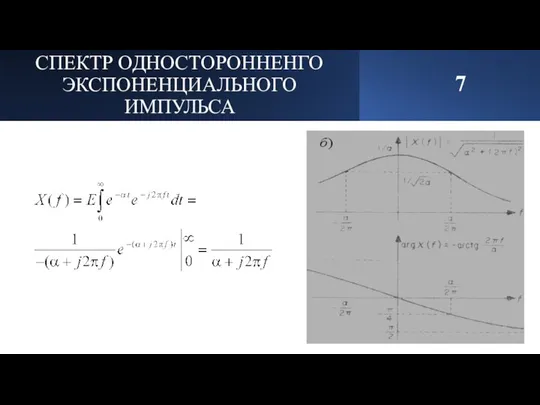
- 8. СПЕКТР ОДНОСТОРОННЕНГО ЭКСПОНЕНЦИАЛЬНОГО ИМПУЛЬСА 7
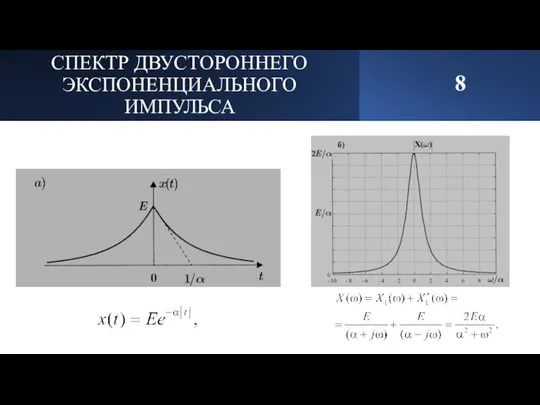
- 9. СПЕКТР ДВУСТОРОННЕГО ЭКСПОНЕНЦИАЛЬНОГО ИМПУЛЬСА 8
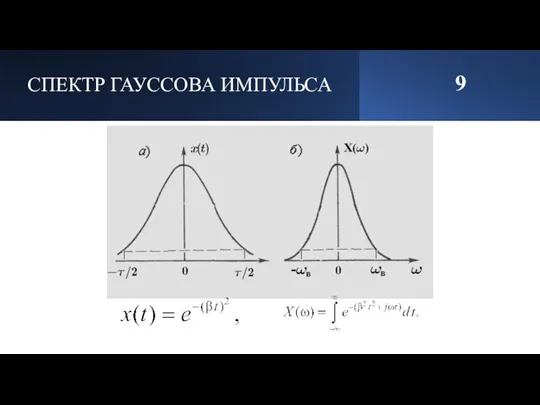
- 10. СПЕКТР ГАУССОВА ИМПУЛЬСА 9
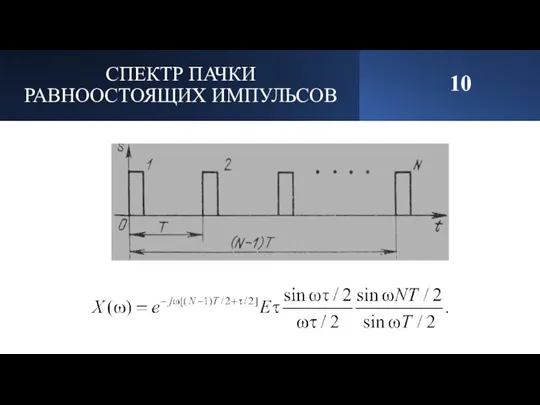
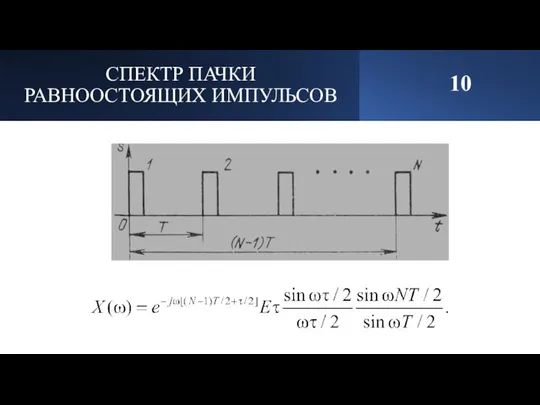
- 11. СПЕКТР ПАЧКИ РАВНООСТОЯЩИХ ИМПУЛЬСОВ 10
- 12. СПЕКТР ПАЧКИ РАВНООСТОЯЩИХ ИМПУЛЬСОВ 10
- 13. КАК ЗАДАТЬ СИГНАЛ ДЛЯ ЛР 1? 11 t1 = 5*10^-6; t2 = 15*10^-6; f0 = 0.5*10^6;
- 15. Скачать презентацию




 Инструкция по получению учебно-методических материалов в личном кабинете студента
Инструкция по получению учебно-методических материалов в личном кабинете студента Презентация на тему Внутренняя политика Ивана Грозного. Последние годы правления.
Презентация на тему Внутренняя политика Ивана Грозного. Последние годы правления.  Мануал по решению основных проблем при переводе с японского на русский
Мануал по решению основных проблем при переводе с японского на русский Путешествие по Смольному монастырю
Путешествие по Смольному монастырю Презентация на тему Собор святой Софии в Константинополе
Презентация на тему Собор святой Софии в Константинополе Дизайн-менеджмент
Дизайн-менеджмент Семинар SLS в Новосибирске. - презентация
Семинар SLS в Новосибирске. - презентация Организация работы классного руководителя
Организация работы классного руководителя Загадки о цветах
Загадки о цветах Как работать с заданиями. Пошаговая инструкция для студентов ФНиДО БГУИР
Как работать с заданиями. Пошаговая инструкция для студентов ФНиДО БГУИР Мы и дорога
Мы и дорога Использование компьютерных технологий в начальной школе
Использование компьютерных технологий в начальной школе www.brianna-trans.com
www.brianna-trans.com Реклама Альфа-Банку
Реклама Альфа-Банку Пищевые продукты, питательные вещества и их превращения в организме
Пищевые продукты, питательные вещества и их превращения в организме Коэффициент графика функции
Коэффициент графика функции Приветствуем участников окружного семинара руководителей ОУ «Формирование единого информационного пространства школы».
Приветствуем участников окружного семинара руководителей ОУ «Формирование единого информационного пространства школы». Паровозик. Рисунок
Паровозик. Рисунок Аналитическо-проектная работа по анализу кадровой политики организации
Аналитическо-проектная работа по анализу кадровой политики организации ЭКОЛОГИЧЕСКОЕ ПРАВО
ЭКОЛОГИЧЕСКОЕ ПРАВО Теорема Пифагора
Теорема Пифагора ОТЧЕТ О РАБОТЕПО ЗАМЕЧАНИЯМ НА ПРОЕКТ«МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПЛАНИРОВАНИЮ И ОРГАНИЗАЦИИ ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ ПР
ОТЧЕТ О РАБОТЕПО ЗАМЕЧАНИЯМ НА ПРОЕКТ«МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПЛАНИРОВАНИЮ И ОРГАНИЗАЦИИ ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ ПР Определитель и действие с ними
Определитель и действие с ними Понятие «контроллинг»
Понятие «контроллинг» Художественная культура Древнего Египта
Художественная культура Древнего Египта Работа школы в режиме Полного Дня
Работа школы в режиме Полного Дня Новгородская земля
Новгородская земля Утверждение тоталитаризма
Утверждение тоталитаризма