Способы проецирования

7.1. Многообразие геометрических форм в природе.
На уроках математики вы уже познакомились с некоторыми геометрическими фигурами.
Под фигурой понимают любую совокупность (множество) точек.
Всякую сложную фигуру можно разделить на более простые.
Если все точки фигуры лежат в одной плоскости, фигуру называют плоской:
треугольник, квадрат и др.
Совокупность точек, расположенных в пространстве, образует пространственную фигуру:
куб, цилиндр и др.
Фигуры в пространстве называют телами.

Предметы, которые нас окружают, детали машин, имеют, как правило, сложную реальную геометрическую форму.
Однако, присмотревшись к ним внимательно, можно заметить, что некоторые из них состоят из одного или нескольких простых геометрических тел или их видоизмененных частей.
Такими геометрическими телами, образующими форму предметов, являются призмы (рис. 22, а), пирамиды (рис. 22, б), цилиндры (рис. 23, а), конусы (рис. 23, б), шары и др.
Рис. 22
Рис. 23

Форма каждого геометрического тела имеет свои характерные признаки.
По ним мы отличаем призму от цилиндра, пирамиду от конуса и т. п.
Эти признаки используются и при построении чертежей геометрических тел или состоящих из них предметов и деталей.
Однако, прежде чем выполнять такие чертежи, выясним, какие правила положены в основу способов их построения.

7.2. Общие сведения о проецировании.
Изображения предметов на чертежах в соответствии с правилами государственного стандарта выполняют по способу (методу) прямоугольного проецирования.
Проецированием будем называть процесс получения проекций предмета.
Рассмотрим пример.
Возьмем в пространстве произвольную точку А и какую-нибудь плоскость.
Обозначим эту плоскость, например, прописной буквой П (пи) греческого алфавита с индексом один - т. е. П1 (рис. 24).
Рис. 24

Плоскость, на которой получается проекция, называется плоскостью проекций.
Прямая АА' называется проецирующим лучом.
С его помощью точка А проецируется на плоскость П1.
Примечание.
Существуют и другие обозначения проекций точек — A1, A2, А3— и плоскостей проекций — Н, V, W.
Указанным способом могут быть построены проекции всех точек любой фигуры.

Так, чтобы получить проекцию А'B' отрезка АВ прямой (рис. 25, а), необходимо провести проецирующие лучи через две точки отрезка - А и В.
При этом, если прямая или ее отрезок совпадают по направлению с проецирующим лучом (отрезок CD на рис. 25, б), они проецируются на плоскость проекций в точку.
Рис. 25

Для построения проекции какой-либо фигуры необходимо через ее точки провести воображаемые проецирующие лучи до пересечения их с плоскостью проекций.
Проекции всех точек фигуры на плоскости и образуют проекцию заданной фигуры.
Рассмотрим, например, получение проекции такой геометрической фигуры, как треугольник (рис. 26).
Рис. 26

В дальнейшем под термином проекция мы будем понимать изображение предмета на плоскости проекций.
Слово «проекция» латинское. В переводе оно означает «бросать (отбрасывать) вперед».
Положите на бумагу какой-нибудь плоский предмет и обведите его карандашом.
Вы получите изображение, соответствующее проекции этого предмета.
Примерами проекций являются фотографические снимки, кинокадры и др.
Изображения предметов, полученные путем проецирования, будем называть проекционными.

7.3. Центральное и параллельное проецирование.
Если проецирующие лучи, с помощью которых строится проекция предмета, исходят из одной точки, проецирование называется центральным (рис. 27).
Рис. 27
Точка, из которой исходят лучи, называется центром проецирования.
Полученная при этом проекция называется центральной.
Центральную проекцию часто называют перспективной.
Примерами центральной проекции являются фотоснимки и кинокадры, тени, отброшенные от предмета лучами электрической лампочки, и др.
Центральные проекции применяют в рисовании с натуры.

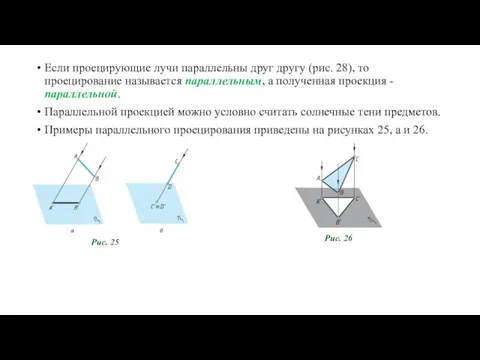
Если проецирующие лучи параллельны друг другу (рис. 28), то проецирование называется параллельным, а полученная проекция - параллельной.
Параллельной проекцией можно условно считать солнечные тени предметов.
Примеры параллельного проецирования приведены на рисунках 25, а и 26.
Рис. 25
Рис. 26

Рис. 28
Строить изображение предмета при параллельном проецировании проще, чем при центральном.
Так, если отрезок АВ (рис. 28) или любая плоская фигура, как, например, на рисунке 29, параллельны плоскости проекций, то их проекции и сами проецируемые фигуры равны.
Рис. 29

При параллельном проецировании все лучи падают на плоскость проекций под одинаковым углом.
Если это любой угол, который не равен 90°, как на рисунке 29 а или на рисунке 25 а, то проецирование называется косоугольным.
В том случае, когда проецирующие лучи перпендикулярны плоскости проекций (см. рис. 29 б), т. е. составляют с ней угол 90°, проецирование называется прямоугольным (см. рис. 26).
Полученная при этом проекция называется прямоугольной.

7.4. Получение аксонометрических проекций.
В технической графике особую группу составляют проекции, которые получены путем параллельного проецирования предмета вместе с осями х, у и z пространственной системы прямоугольных координат на произвольную плоскость (рис. 30).
Рис. 30
Обозначим ее П0.
Полученную таким образом проекцию на плоскости П0 называют аксонометрической.
В зависимости от направления проецирования по отношению к плоскости проекций аксонометрические проекции могут быть как прямоугольными, так и косоугольными.
Слово «аксонометрия» - греческое. В переводе оно означает «измерение по осям».

Проекции х0, у0 и z0 осей координат на плоскости проекций называют аксонометрическими.
Когда строят аксонометрические проекции предметов, размеры откладывают по осям или параллельно им.
Аксонометрические проекции относят к числу наглядных изображений.
По ним можно легко получить общее представление о внешней форме предмета.
Однако на аксонометрических проекциях предметы получаются с искажениями.
Например, окружности проецируются в эллипсы, прямые углы - в тупые или острые.
Искажаются и некоторые размеры предмета.
Поэтому такие проекции применяют в основном при выполнении технических рисунков.
Для получения изображений на чертежах используют метод прямоугольного проецирования на одну, две и более плоскости проекций.

Вопросы:
Какие геометрические тела вам известны?
Посмотрите вокруг себя и найдите в форме окружающих предметов простые геометрические тела.
Что представляет собой проецирование?
Как строить на плоскости проекцию точки? проекцию фигуры?
Какое проецирование называется центральным? параллельным? косоугольным? прямоугольным?
Почему строить изображение в параллельной проекции проще, чем в центральной?
Какие проекции называют аксонометрическими?
Какие аксонометрические проекции получаются в зависимости от направления проецирования?