Способы решения уравнений с помощью компьютера

Цели урока:
расширение и систематизация знаний учащихся о применении компьютера для решения задач, способах решения алгебраических уравнений с помощью компьютера.
Совершенствование навыков составления и реализации программ на языке Турбо Паскаль, навыков использования программы Excel для решения задач.
Создание условий для развития исследовательской, творческой, познавательной деятельности учащихся.

Задача: решить уравнение вида
Какими способами можно решить уравнение?
Что значит решить уравнение аналитически?
Что значит решить уравнение графически?

Из каких этапов складывается решение задач с помощью ПК?
Постановка задачи
Разработка формальной модели
Построение компьютерной модели
Компьютерный эксперимент
Анализ результатов
Корректировка модели

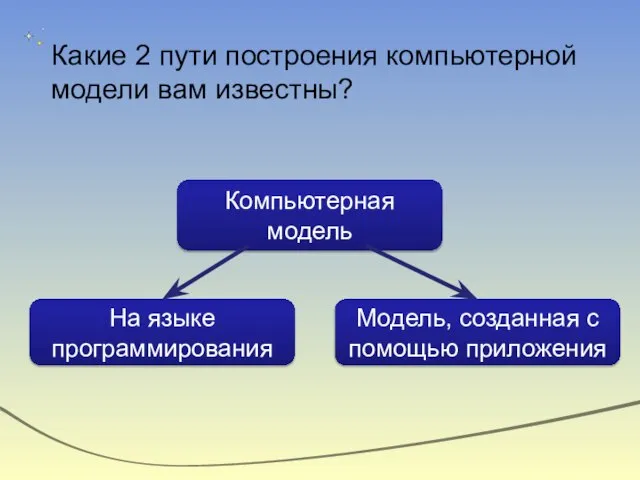
Какие 2 пути построения компьютерной модели вам известны?

Из каких этапов складывается графическое решение уравнения с помощью программы Excel?
Построение таблицы значений
Построение графиков функций
Определение корней уравнения(точек пересечения графиков)

Решим уравнение вида sin(2*α)=0.5*(sin(α)+cos(α))
Этапы решения уравнения с помощью численных методов:
отделение корней, т.е. отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения;
вычисление корня с заданной точностью.

Численные методы приближенного вычисления корней уравнения:
Метод половинного деления
Метод касательных
Метод хорд
Метод секущих
Метод хорд и касательных

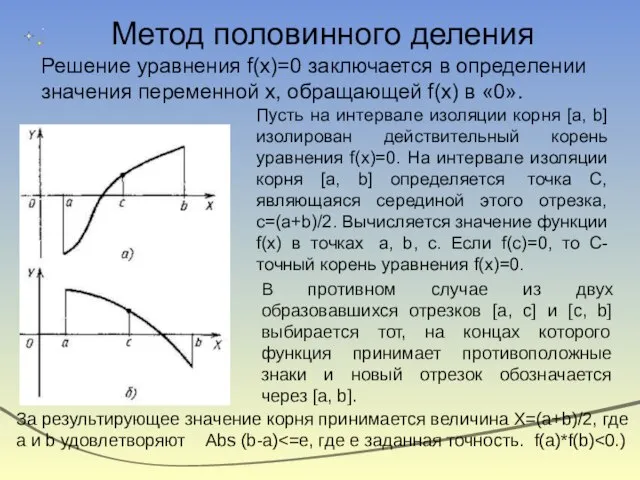
Метод половинного деления
Решение уравнения f(x)=0 заключается в определении значения переменной х, обращающей f(x) в «0».
Пусть на интервале изоляции корня [a, b] изолирован действительный корень уравнения f(x)=0. На интервале изоляции корня [a, b] определяется точка С, являющаяся серединой этого отрезка, c=(a+b)/2. Вычисляется значение функции f(x) в точках a, b, c. Если f(c)=0, то С-точный корень уравнения f(x)=0.
В противном случае из двух образовавшихся отрезков [a, c] и [c, b] выбирается тот, на концах которого функция принимает противоположные знаки и новый отрезок обозначается через [a, b].
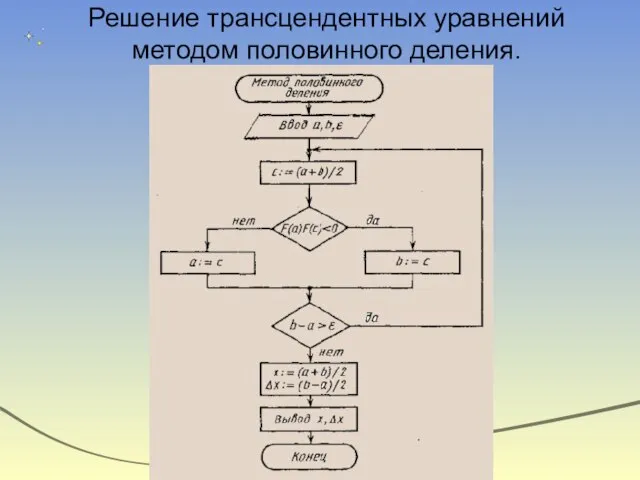
За результирующее значение корня принимается величина X=(a+b)/2, где a и b удовлетворяют Abs (b-a)<=e, где е заданная точность. f(a)*f(b)<0.)

Решение трансцендентных уравнений методом половинного деления.

Практическое закрепление.
1 группа: Отделяет корни уравнения: составляет таблицу значений функции на интервале от 0 до 1,95 с шагом 0,15 и выделяет соседние значения аргументов для которых значения функции имеют разные знаки, то есть значения аргументов между которыми находится нуль функции.
2 группа: Определяет корни графически на интервале от 0 до 1,95 с шагом 0,15.
3 группа: В среде Турбо Паскаль реализует составленную программу и определяет корни с точность 0,001.

Подведение итогов занятия
Какие способы решения уравнений рассмотрели на уроке?
Из каких этапов складывается графическое решение с использованием программы Excel?
Какие численные методы используются для решения уравнений?
В чем сущность метода половинного деления?
Какой способ организации действий использован в составленной программе?
В чем преимущество численных методов перед графическим методом отыскания корней?
Что не учитывает программа составленная на уроке?