Справочный материал

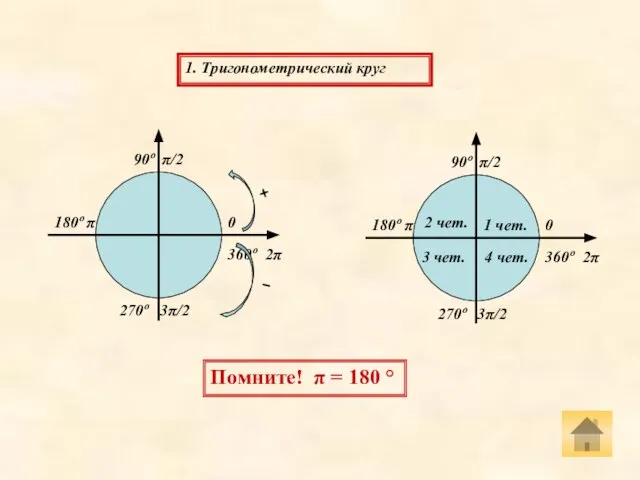
0
90º π/2
180º π
270º 3π/2
360º 2π
1. Тригонометрический круг
0
90º π/2
180º π
270º 3π/2
360º 2π
1 чет.
2 чет.
3 чет.
4 чет.
Помните! π = 180 °

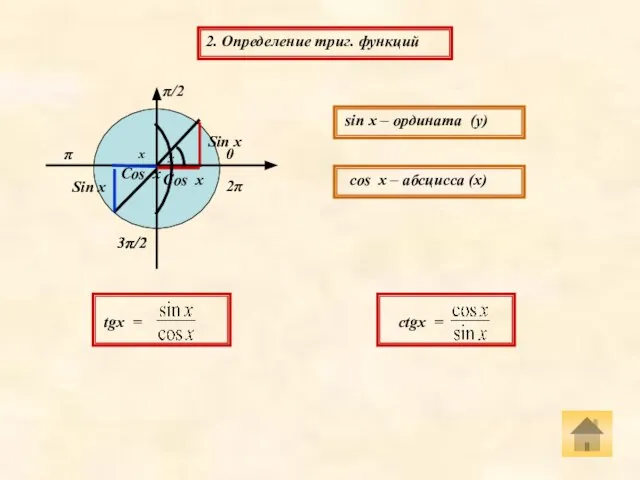
2. Определение триг. функций
Sin х
Cos х
0
π/2
π
3π/2
2π
3π/2
Cos х
Sin х
sin х – ордината (у)
cos х – абсцисса (х)

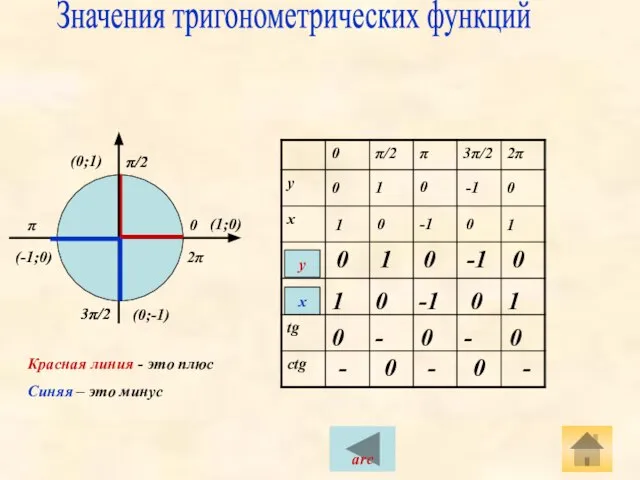
π/2
0
π/2
π
3π/2
2π
3π/2
Красная линия - это плюс
Синяя – это минус
0
1
0
1
0
-1
-1
0
0
1
y
x
0 1 0 -1 0
1 0 -1 0 1
0 - 0 - 0
- 0 - 0 -
Значения тригонометрических функций
(1;0)
(0;1)
(-1;0)
(0;-1)
arc

Табличные значения
Значения тригонометрических функций
1
1
Ряд синуса
Запомни!
Для косинуса поменяйте крайние значения
Ряд тангенса
Для котангенса поменяйте крайние значения

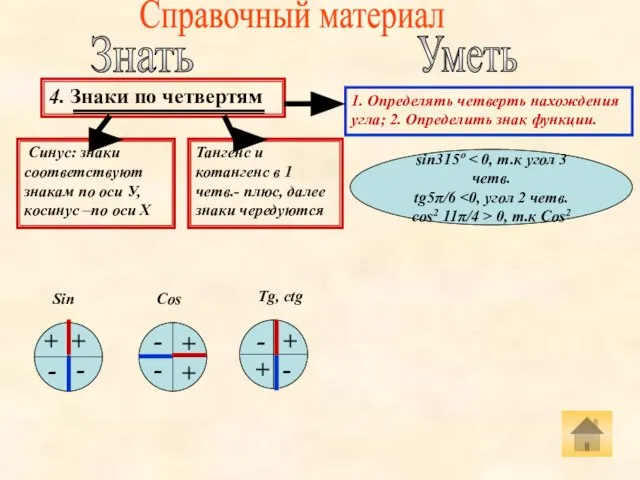
Справочный материал
Знать
Уметь
4. Знаки по четвертям
Синус: знаки соответствуют знакам по оси У, косинус –по оси Х
Тангенс и котангенс в 1 четв.- плюс, далее знаки чередуются
1. Определять четверть нахождения угла; 2. Определить знак функции.
sin315º < 0, т.к угол 3 четв.
tg5π/6 <0, угол 2 четв.
cos2 11π/4 > 0, т.к Cos2

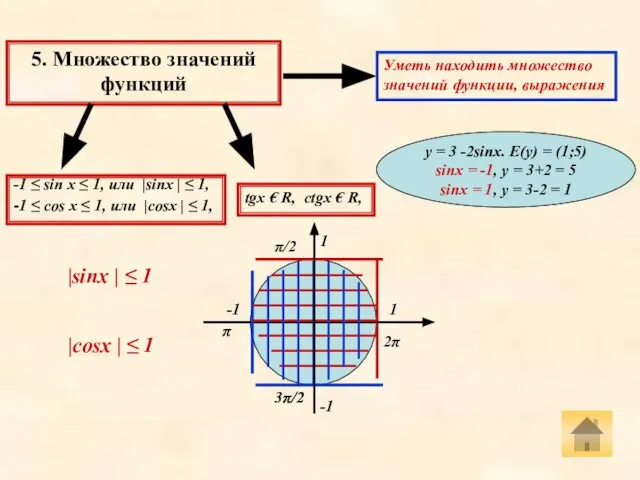
5. Множество значений функций
tgx € R, ctgx € R,
-1 ≤ sin х ≤ 1, или |sinx | ≤ 1,
-1 ≤ cos х ≤ 1, или |cosx | ≤ 1,
Уметь находить множество значений функции, выражения
y = 3 -2sinx. E(y) = (1;5)
sinx = -1, y = 3+2 = 5
sinx = 1, y = 3-2 = 1
π
3π/2
2π
3π/2
π/2
1
-1
1
-1
|sinx | ≤ 1
|cosx | ≤ 1

Период
Период – это число, при прибавлении которого к аргументу значение функции не изменяется.
f(x +Т) = f(x)
Если Т – период, то Tn для n € Z тоже период. Считается Т – наименьший период
Так как f(x +Тn) = f(x), то Tn можно опустить
sin, cos Т = 2π
tg, ctg Т = π

Четность, нечетность
Синус, тангенс, котангенс – функции
нечетные.
Минус у угла можно вынести за знак функции
Примеры
1. sin ( – х) = - sin х
2. sin ( π/4 – х) = - sin ( х - π/4 )
4. cos (-7π/3)= cos 7π/3 = cos (2π + π/3) = cos π/3 = ½
5. cos (-β) = cos β
6. ctg ( 2α - π/2) = - ctg (π/2 - 2α )
Косинус – функция
четная.
Минус у угла можно опустить

Область определения
Синус, косинус
D(y) = R
Функции непрерывны на R
Tангенс
D(y) = R, x ≠ π/2 + πn
x = π/2 + πn – вертикальная асимптота
Котангенс
D(y) = R, x ≠ πn
x = πn – вертикальная асимптота
tgx – определен при cosx ≠ 0
ctgx – определен при sinx ≠ 0

Тригонометрические формулы
1. Формулы одного аргумента
sin2□ + cos2□ = 1
sin2□ = 1 - cos2□
cos2□ = 1 - sin2□
Под □ понимается любой угол ( х, 2х, α/2 и т. д.)

Тригонометрические формулы
Составьте формулы:
2. Формулы сложения
sin ( α ± β) =
sin cos
sin cos
α
β
cos ( α ± β) =
cos cos
sin sin
α
α
α
β
β
β
±
tg ( α ± β) =
б) поставьте трафарет, проговорите: «синус на косинус, косинус на косинус, синус на синус;
а) сначала поставьте знак;
в) расставьте углы
.
Запомните!
Для sin − синус на косинус, знак тот же;
Для cos − косинус на косинус, синус на синус, знак противоположный.

Тригонометрические формулы
Составьте формулы:
3. Формулы двойного угла
cos 2 =
tg 2 =
2α
sin 2 =
а) определите углы: (половина, двойной ) ;
в) составьте формулы
б)используя формулы сложения, выведите формулы для угла (α + α);
2
____________
____________
двойной угол
половина угла
____________
____________
половина угол
двойной угол
2α
= α
х
.
Запомните!
Для sin − два, синус на косинус, ;
Для cos − косинус квадрат минус синус квадрат.
Угол справа в два раза меньше

Тренинг
1. Найдите половину угла:
2β
х
30º
120º
8β
4х
х – π/8
х – π/4
2. Примените формулу двойного угла sin х =
2sin х/2 cos х/2
2sin 2х cos 2х
cos х =
cos 22х - sin 22х
cos 2х/2 - sin 2х/2
sin 2β = 2 2sin cos
2β
β
β
cos 4х = cos 2 - sin 2
2х
2х
8х
8х
sin х cos х =
2 sin2х
sin 2х - cos 2х =
- cos 2х
cos х/2
2β
х
30º
х – π/8
Помните! Если в выражении встречается sinxcosx, примените формулу двойного угла синуса

Тригонометрические формулы
2. Формулы половинного угла. (понижения степени)
cos 2 =
tg 2 =
sin 2 =
2
2
-
+
.
Запомните!
Для sin 2 −единица минус cos ;
Для cos 2 − единица плюс cos;
Угол справа в два раза больше

Тригонометрические формулы
Составьте формулы:
4. Формулы перевода суммы в произведение
а) для синуса и косинуса запишите 2 и - 2;
г) составьте формулу для тангенса: синус, деленный на косинус
б) запишите трафарет ;
-
sin α + sin β =
sin α - sin β =
cos α - cos β =
cos α + cos β =
tg α + tg β =
tg α - tg β =
в) расставьте полу сумму углов, полу разность
2
2
2
2
sin cos
sin cos
cos cos
sin sin
2
2
2
-2
.
Запомните!
Для sin − sin на cos ;
Для cos − cos на cos или sin на sin ;
Полу сумма , полу разность углов

Тригонометрические формулы
Составьте формулы:
4. Формулы перевода произведения в сумму
а) для синуса и косинуса запишите ½ ;
б) запишите трафарет ;
-
sin α sin β =
cos α cos β =
г) расставьте разность и сумму углов
½
(sin cos )
(cos cos )
sin α cos β =
½
½
(α – β)
(α – β)
(α – β)
(α + β)
(α + β)
(α + β)
+
+
(cos cos )
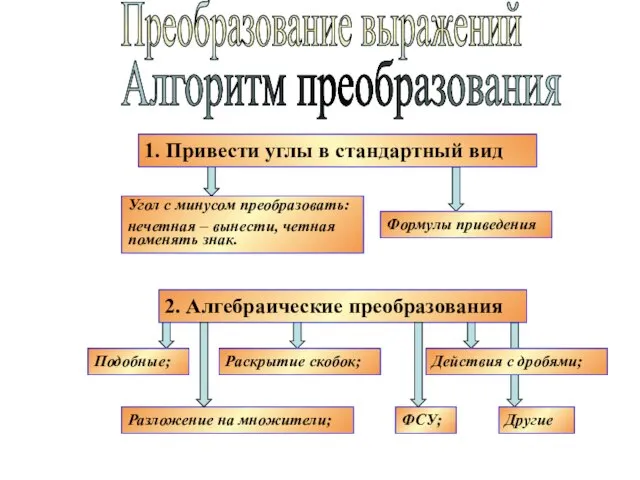
в) Расставьте знаки между функциями

Преобразование выражений
Алгоритм преобразования
1. Привести углы в стандартный вид
Угол с минусом преобразовать:
нечетная – вынести, четная поменять знак.
Формулы приведения
2. Алгебраические преобразования
Подобные;
Раскрытие скобок;
Действия с дробями;
Разложение на множители;
ФСУ;
Другие

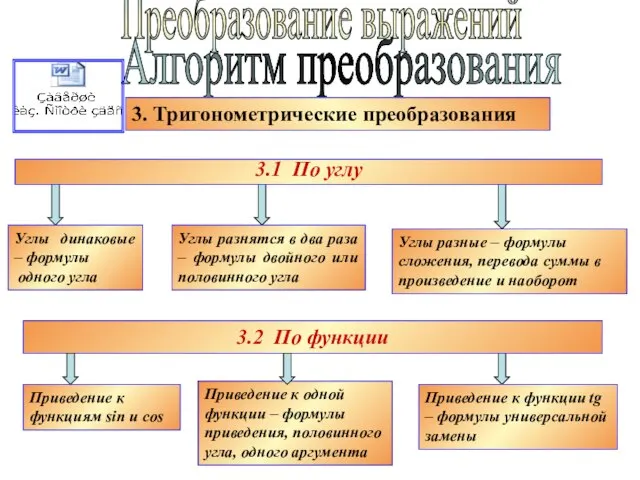
Преобразование выражений
Алгоритм преобразования
3. Тригонометрические преобразования
3.1 По углу
3.2 По функции
Углы динаковые – формулы одного угла
Углы разнятся в два раза – формулы двойного или половинного угла
Углы разные – формулы сложения, перевода суммы в произведение и наоборот
Приведение к функциям sin и cos
Приведение к одной функции – формулы приведения, половинного угла, одного аргумента
Приведение к функции tg – формулы универсальной замены

Преобразование выражений
1) Найдите 13 cos α + 1, если sin α = 5/13 , π/2 ≤ α ≤ π
2) Упростить выражение 1 - tg х sin х cos х
3) Упростите выражение (1 + tg 2α )(1 – cos2α )
7) Упростите выражение sin4α – cos 4α
6)Упростите выражение
Тренинг

1)Найдите 13 cos α + 1, если sin α = 5/13 , π/2 ≤ α ≤ π
Чтобы найти значение 13 cos α + 1, надо узнать cos α .
Так как α принадлежит второй четверти, то cos α < 0, следовательно,
13 cos α + 1 = 13∙(- 12/13) + 1 = - 11
Преобразование выражений

2. Упростить выражение 1 + tg х sin х cos х
1 - sin 2х = cos 2х
Тригонометрия
Алгебра
Тригонометрия

Используем формулы:
3) Упростите выражение (1 + tg 2α )(1 – cos2α )
Алгебра отсутствует
Тригонометрия
1 + tg 2α = 1/cos 2 α
1 – cos2α = sin 2 α
(1 + tg 2α )(1 – cos2α ) =

Используем формулы:
Алгебра отсутствует
Тригонометрия
Sinα cos β + Sinβ cos α = sin (α+β)
sinα cos α = ½ sin 2α
Подставим значения:

Алгебра
Сложим дроби:
cos 15○
sin15○
Используем формулы:
Тригонометрия
cos2 α – sin2α = cos 2α
sinα cos α = ½ sin 2α

6)Упростите выражение
Алгебра отсутствует
Тригонометрия
Применим формулы двойного угла косинуса и основное тригонометрическое тождество
cos 2α = cos2 α - sin2 α
Углы разнятся в два раза.
sin2 α + cos2 α = 1

Алгебра
Применим разность квадратов
Используем формулы:
Тригонометрия
cos2 α – sin2α = cos 2α
sin2 α + cos2 α = 1
7) Упростите выражение sin4α – cos 4α
sin4α – cos 4α = (sin2α – cos 2α)(sin2α + cos 2α )
sin4α – cos 4α = (sin2α – cos 2α)(sin2α + cos 2α ) = - cos 2α

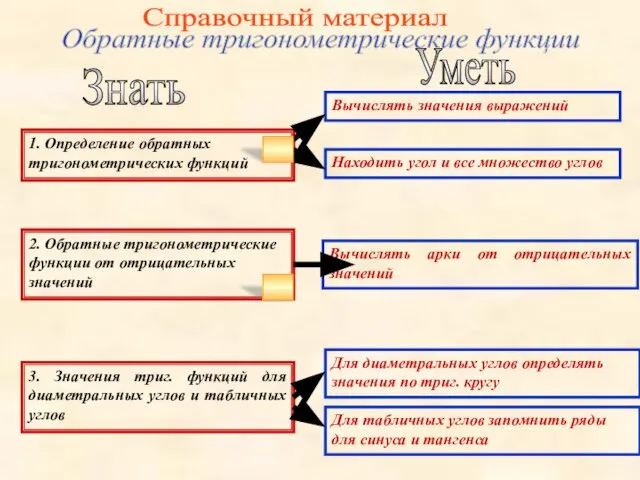
Справочный материал
Знать
Уметь
1. Определение обратных тригонометрических функций
Вычислять значения выражений
Находить угол и все множество углов
2. Обратные тригонометрические функции от отрицательных значений
Вычислять арки от отрицательных значений
3. Значения триг. функций для диаметральных углов и табличных углов
Для диаметральных углов определять значения по триг. кругу
Для табличных углов запомнить ряды для синуса и тангенса
Обратные тригонометрические функции

arcsin а = φ, sin φ = а. -π/2 ≤ φ ≤ π/2
arccos а = φ, cos φ = а. 0 ≤ φ ≤ π
arctg а = φ, tg φ = а. -π/2 < φ < π/2
arcctg а = φ, ctg φ = а. 0 < φ < π
Запомни!
arc… - это угол

arcsin(- а) = - arcsin а
arccos(- а) = π - arccos а
arctg(- а) = - arctg а
arcctg(- а) = π - arcctg а
Запомни!
Считая а > 0,
Для sin и tg
Для cos и ctg
Минус вынести
Пи минус арк

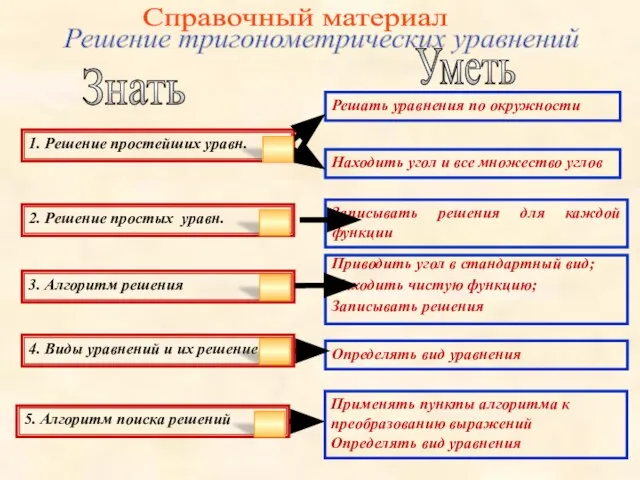
Справочный материал
Знать
Уметь
1. Решение простейших уравн.
Решать уравнения по окружности
Находить угол и все множество углов
2. Решение простых уравн.
Записывать решения для каждой функции
3. Алгоритм решения
Приводить угол в стандартный вид;
Находить чистую функцию;
Записывать решения
Определять вид уравнения
Решение тригонометрических уравнений
4. Виды уравнений и их решение
5. Алгоритм поиска решений
Применять пункты алгоритма к преобразованию выражений Определять вид уравнения

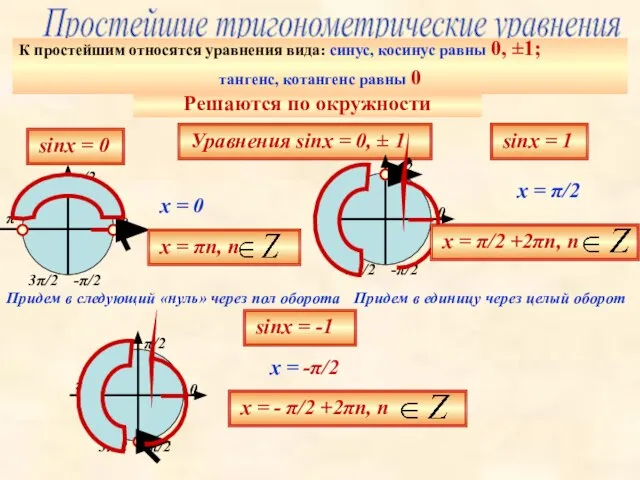
Простейшие тригонометрические уравнения
Уравнения sinх = 0, ± 1
К простейшим относятся уравнения вида: синус, косинус равны 0, ±1;
тангенс, котангенс равны 0
Решаются по окружности
sinх = 0
х = 0
Придем в следующий «нуль» через пол оборота
sinх = 1
х = π/2
Придем в единицу через целый оборот
sinх = -1
х = -π/2

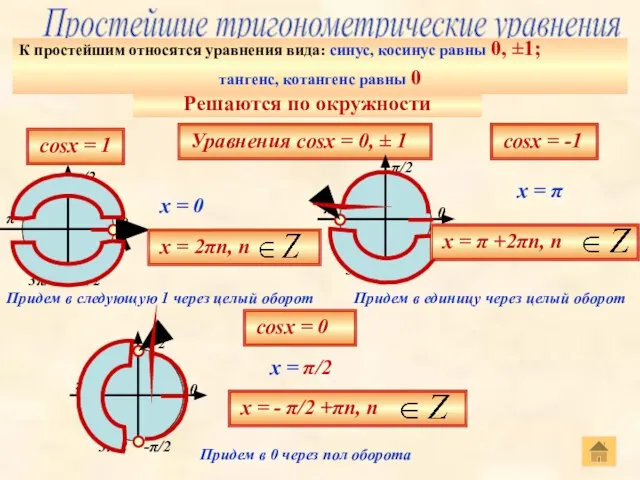
Простейшие тригонометрические уравнения
Уравнения cosх = 0, ± 1
К простейшим относятся уравнения вида: синус, косинус равны 0, ±1;
тангенс, котангенс равны 0
Решаются по окружности
cosх = 1
х = 0
Придем в следующую 1 через целый оборот
cosх = -1
х = π
Придем в единицу через целый оборот
cosх = 0
х = π/2
Придем в 0 через пол оборота

Минус единица в степени...
Плюс, минус …
арктангенс
арккотангенс
Считая а > 0,
Для уравнения sinх =а
Для уравнения cosх = а
x = arcsina + πn, где n Z
(-1)n
x = arcсosa + 2πn, где n Z
±
Для уравнений tgх =а, ctgx = a
Для уравнений sinx= a, tgх =а, ctgx = a
+ πn
Для уравнения cosx = a
+2πn
Тригонометрические уравнения
Запомни!

Минус единица в степени n +1…
Плюс, минус, скобка, пи минус…
минус арктангенс
пи минус арккотангенс
Запомни!
Считая а < 0,
Для уравнения sinх =а
Для уравнения cosх = а
x = arcsin|a| + πn, где n Z
(-1)n+1
x = (π - arcсos|a|) + 2πn, где n Z
±
Для уравнений tgх =а, ctgx = a
x = аrctg|a| + πn, где n Z
-
x = π аrcctg|a| + πn, где n Z
-

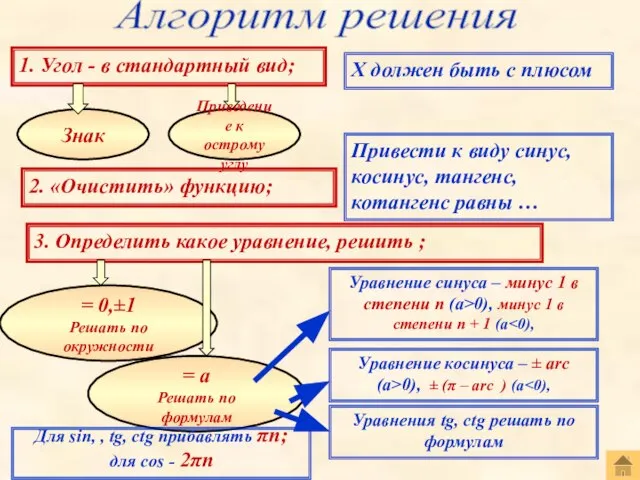
Алгоритм решения
1. Угол - в стандартный вид;
Х должен быть с плюсом
Знак
Приведение к
острому углу
2. «Очистить» функцию;
Привести к виду синус, косинус, тангенс, котангенс равны …
3. Определить какое уравнение, решить ;
= 0,±1
Решать по окружности
= а
Решать по формулам
Уравнение синуса – минус 1 в степени n (a>0), минус 1 в степени n + 1 (a<0),
Уравнение косинуса – ± аrc (a>0), ± (π – arc ) (a<0),
Уравнения tg, ctg решать по формулам
Для sin, , tg, ctg прибавлять πn;
для cos - 2πn

Тренинг
1. Решите уравнения, отвечая на вопросы:
Уравнение sin
Уравнение cos
Уравнение tg
(-1)n arcsin…
± arccos…
arctg…
πn
πn
2πn
2πn
πn