Содержание
- 2. Для чего нужна статистика? Для строгого доказательства эффективности методов диагностики и лечения (какому проценту больных помогает
- 3. Этапы исследования: Планирование и организация исследования; Проведение наблюдения (собственно исследование); Обработка и анализ данных, выводы, оформление
- 4. Простейшие ошибки: Отсутствие контрольной группы; Использование неслучайных выборок; Пренебрежение статистической проверкой гипотез.
- 5. Вероятностный характер В результате применения статистических методов мы получаем не истину в последней инстанции, а оценку
- 6. ВХОД→ПРОЦЕСС→ВЫХОД Врач Иванов лечил n пациентов с исходами «выздоровление», «улучшение состояния», «без изменений», «ухудшение», «летальный исход».
- 7. Корректность модели: Если у врача X больше благоприятных исходов, чем у врача Y , означает ли
- 8. Гипотезы: Гипотеза – предположение о сущности данного факта (или ряда фактов). Гипотеза, принятая исследователем называется рабочей
- 9. Примеры гипотез (Стругацкие. «Стажеры»): В древней пещере «первояпонцев» обнаружено множество небольших окаменевших следов босых ног, а
- 10. Единицы и признаки наблюдения Единицы наблюдения – отдельные случаи изучаемого явления. Например, при исследовании заболеваемости раком,
- 11. Типы признаков: Количественные признаки измеряются числовыми значениями (например, возраст, рост, вес, давление). Порядковые признаки – могут
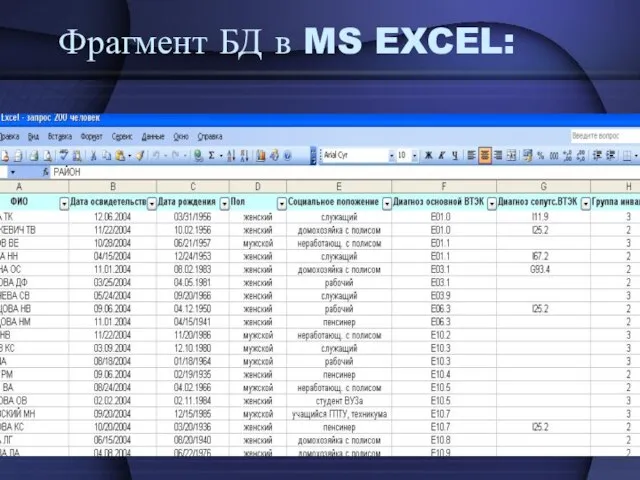
- 12. База данных (БД): БД – формализованная таблица, состоящая из единиц наблюдения с их признаками; Важно: в
- 13. Фрагмент БД в MS EXCEL:
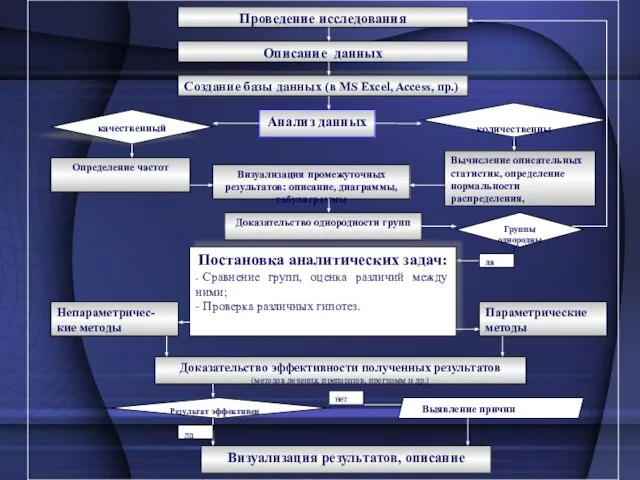
- 14. Основные типы статистических задач: Как сжато описать данные? 2. Статистическая оценка значимости различий признаков в группах,
- 16. Принцип действия критериев: Сравниваются нужные признаки в соответствующем виде эксперимента. Проверяется нулевая гипотеза. Находится фактическая вероятность
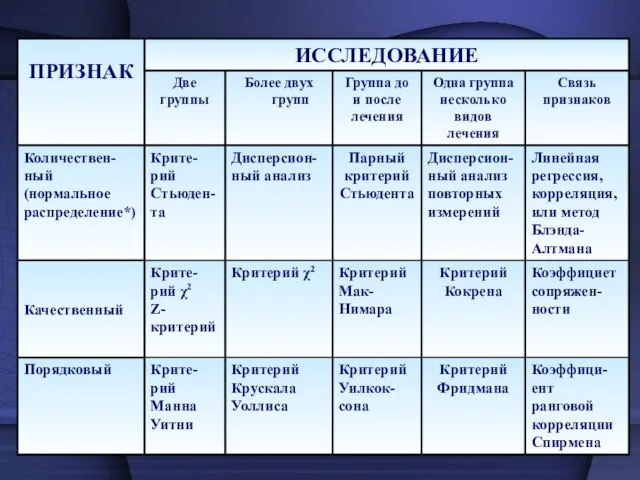
- 17. Как выбрать метод? Если Вы имеете дело с порядковыми и качественными признаками, то подходят только непараметрические
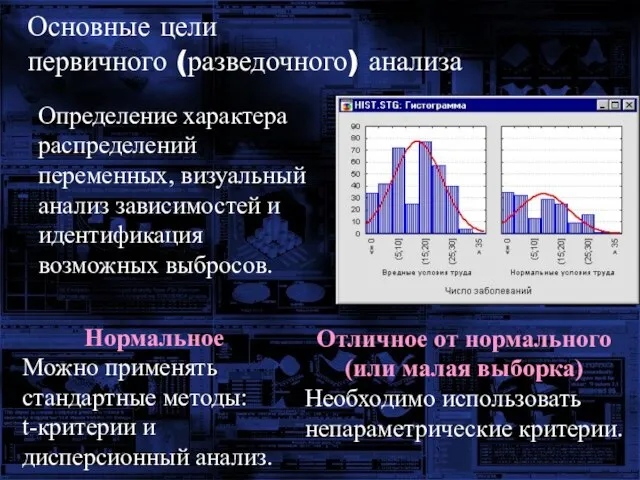
- 18. Основные цели первичного (разведочного) анализа Определение характера распределений переменных, визуальный анализ зависимостей и идентификация возможных выбросов.
- 20. Примеры статистических задач: Задача 1. В группе из 20 человек, вакцинированных от гриппа, заболело 4 человека,
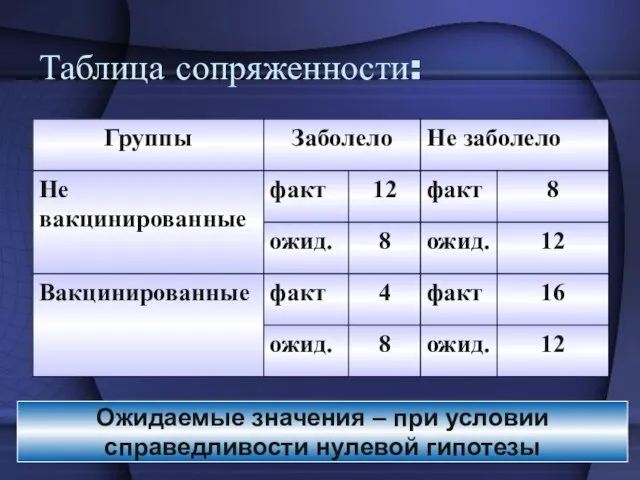
- 21. Таблица сопряженности: Ожидаемые значения – при условии справедливости нулевой гипотезы
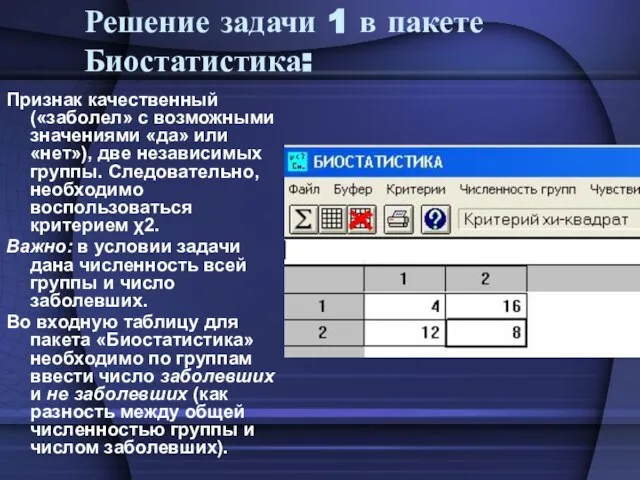
- 22. Решение задачи 1 в пакете Биостатистика: Признак качественный («заболел» с возможными значениями «да» или «нет»), две
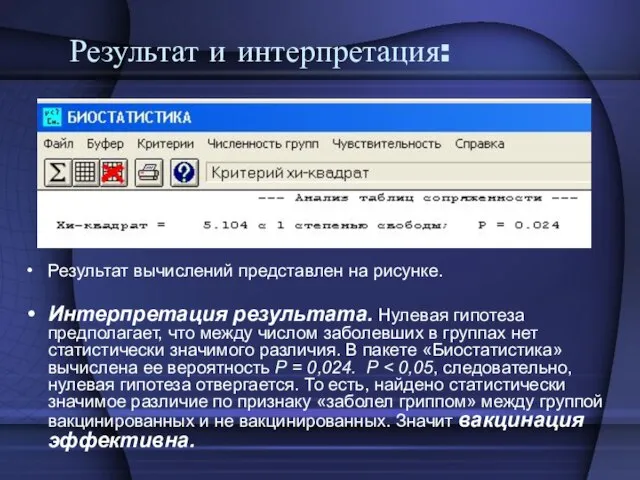
- 23. Результат и интерпретация: Результат вычислений представлен на рисунке. Интерпретация результата. Нулевая гипотеза предполагает, что между числом
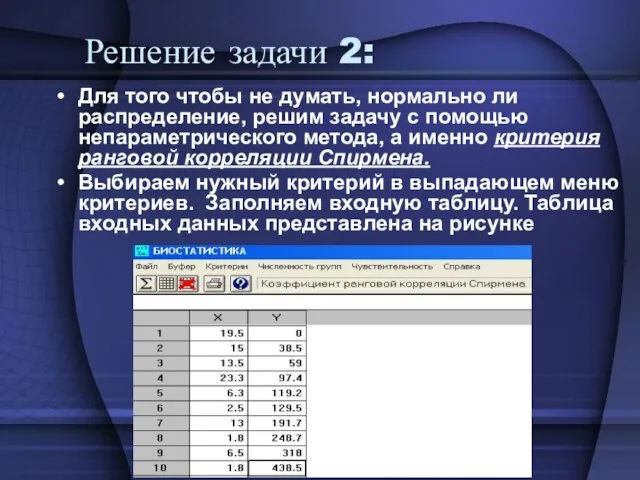
- 24. Задача 2. Существует ли связь между проницаемостью сосудов сетчатки (Х) и электрической активностью сетчатки (Y)? Х={19.5,
- 25. Решение задачи 2: Для того чтобы не думать, нормально ли распределение, решим задачу с помощью непараметрического
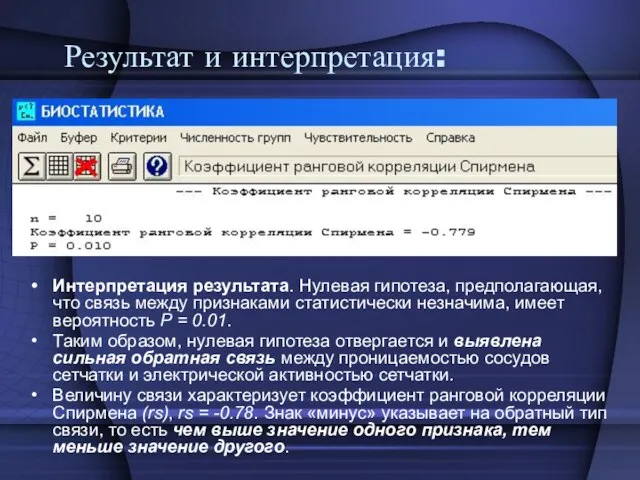
- 26. Результат и интерпретация: Интерпретация результата. Нулевая гипотеза, предполагающая, что связь между признаками статистически незначима, имеет вероятность
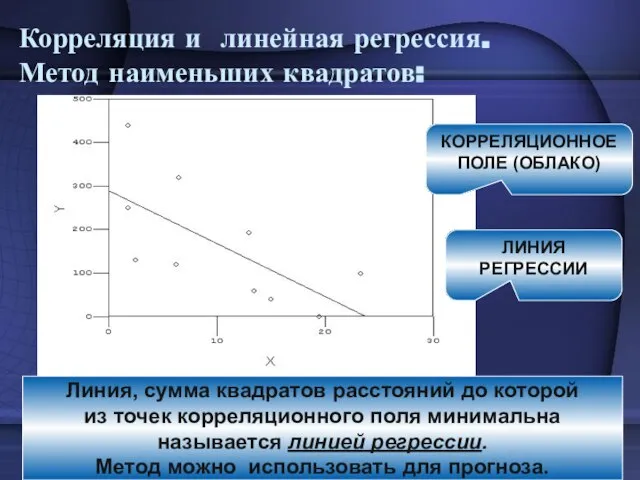
- 27. Корреляция и линейная регрессия. Метод наименьших квадратов: ЛИНИЯ РЕГРЕССИИ КОРРЕЛЯЦИОННОЕ ПОЛЕ (ОБЛАКО) Линия, сумма квадратов расстояний
- 28. Контрольные вопросы 1. Цель исследования определяется на этапе: - планирования и организации исследования - проведения наблюдения
- 29. 2. Объект наблюдения, это: - отдельный случай изучаемого явления - явление, подлежащее исследованию - качественный признак
- 30. 3. Единица наблюдения, это: - количественный признак наблюдения; - явление, подлежащее исследованию; - отдельный случай изучаемого
- 31. 4.Сплошное исследование: - изучает все единицы, входящие в объект наблюдения; - не имеет цели; - изучает
- 32. 5. Выборочное исследование: - выбирает вид наблюдения; - изучает все единицы, входящие в объект наблюдения; -
- 33. 6. Число единиц наблюдения должно быть: - очень большим; - очень маленьким; - оптимальным (не слишком
- 34. 7. Точность результата: - приближение, с которым можно говорить о подлинности результата; - порядковый признак наблюдения;
- 35. 8. Научная гипотеза: - рассказ об исследовании; - метод анализа данных; - предположение о сущности факта
- 36. 9. Что такое вероятность события А?: - частота события А при достаточно большом числе экспериментов; -
- 37. 10. Статистические результаты, как правило: - точные; - вероятностные; - невозможно описать; - не встречаются в
- 38. 11. Нулевая гипотеза: - принимается в статистике в качестве рабочей гипотезы; - принимается в качестве альтернативной
- 39. 12. Критический уровень значимости: - максимально приемлемая вероятность отвергнуть справедливую нулевую гипотезу (обычно в мед. исследованиях
- 40. 13. Если условия экспериментов неоднородны: - нельзя сравнивать их исходы; - эксперименты надо объединять; - исследования
- 41. 14. Количественный признак: - выражается и измеряется числовыми значениями; - измеряется в шкалах (ранжируется); - не
- 42. 15. Качественный признак: - выражается и измеряется числовыми значениями; - измеряется в шкалах (ранжируется); - не
- 43. 16. Порядковый признак: - выражается числовыми значениями; - измеряется в шкалах (ранжируется); - не может быть
- 44. 17. База данных: - таблица, содержащая единицы наблюдения и характеризующие их признаки; - полигон проведения эксперимента;
- 45. 18. Статистика может: - улучшить выборку; - дать статистическое оценивание результатов исследования; - Исправить ошибки в
- 46. 19. Статистика не может: - Исправить ошибки в измерениях; - провести статистическое оценивание; - выполнить Проверку
- 47. 20. Возможные проблемы статистической обработки: - сравнение групп; - некорректное использование статистических методов; - вычисление описательных
- 48. 21. Возможная статистическая ошибка: - вычисление описательных статистик количественных признаков; - расчет частот качественных признаков; -
- 49. 22. Основные описательные статистики количественного признака, это: - среднее, стандартное отклонение, ошибка среднего, процентили (нижний квантиль,
- 50. 23. Распределение признака близко к нормальному, если: - выборка представительна; - среднее признака близко к медиане
- 51. 24. Параметрические методы применяют только для анализа: - качественных признаков; - порядковых признаков; - нерепрезентативных выборок;
- 52. 25. Непараметрические методы применяют для анализа: - объема выборки; - качественных, порядковых признаков и количественных, если
- 53. 26. Рандомизированное исследование, это: - исследование со случайно отобранной контрольной группой; - ретроспективное исследование; - проспективное
- 54. 27. Группы независимы, если: - единицы наблюдения основной и контрольной групп различны; - исследуются одни и
- 55. 28. При сравнении нескольких независимых групп с нормальным распределением признака нужно применять: - критерий Стьюдента; -
- 56. 29. Поправка Бонферрони используется: - в критерии Хи-квадрат; - в корреляционном анализе; - при применении критерия
- 57. 30. Можно ли применять парный критерий Стьюдента для независимых выборок? - да; - нет; - если
- 58. 31. Если сравнивают две независимые группы с качественным дихотомическим признаком: - применяют критерий Хи-квадрат с поправкой
- 59. 32. Чувствительность критерия проверяется: - если различия в группах выявлены; - если найденные различия статистически незначимы;
- 60. 33. Если различий не выявлено при чувствительности 90%, значит: - на самом деле различия есть; -
- 61. 34. Линейная регрессия применяется: - для вычисления прогнозных значений количественных признаков с нормальным распределением; - нахождения
- 62. 35. Экспорт данных: - перевод данных из одной компьютерной программы в другую; - выезд за границу;
- 63. 36. Что означает репрезентативность выборки: - идет сравнение "коров с курицами«; - однородность выборки; выборка отражает
- 64. 37. В статистическом анализе наиболее важно: - уметь корректно поставить задачу исследования, выбрать нужный метод; -
- 65. 38. Связь между степенью тяжести послеоперационного осложнения и временем восстановительного периода в группе оперированных можно найти
- 66. 39. От чего зависит выбор статистического критерия: - от типа признака и вида исследования; - от
- 67. 40. Метод многокритериального выбора "Анализ иерархий" можно применить: - для определения цели исследования; - для вычисления
- 68. 41. Какая из программ наиболее мощная для проведения статистического анализа: - MS Excel; - Биостатистика; -
- 69. 42. Нормально ли распределение: 1,1,1,1,1,1,1,1,1,5,10,10: - да; нет; не знаю; - сложный вопрос.
- 70. 43. Чему равен критический уровень значимости (р) в классическом медицинском исследовании, если для трех групп корректно
- 71. 44. Какой метод статистического анализа следует применить для сокращения числа переменных (редукции данных)? - факторный анализ;
- 72. 45. Что значит «выявлены статистически значимые различия признака в группах сравнения»? - уровень значимости различия р
- 73. 46. Можно ли применить критерий Стьюдента к сравнению признака «рост» с признаком «вес»? - можно; -
- 74. 47. Формула критерия Стьюдента - работает на разности рангов признаков; - основана на разности средних значений
- 75. 48. Таблица сопряженности, это - число возможных сочетаний числа выборок и значений признака; - возможные значения
- 76. 49. Что такое «ожидаемое значение признака» в таблице сопряженности? - фактическое значение признака; - критическая величина
- 77. 50. Что такое «наблюдаемое значение признака» в таблице сопряженности? - фактическое значение признака; - критическая величина
- 78. 51. Критерий хи-квадрат нельзя применять, если - таблица сопряженности имеет размерность больше, чем 2?2; - сравниваются
- 79. 52. Точный критерий Фишера применяется - если находится связь признаков; - если вы хотите построить график;
- 80. 53. Признак называется дихотомическим, если он - принимает одно из двух возможных значений; - количественный; -
- 81. 54. Если сравнивают качественный дихотомический признак в двух независимых группах: - применяют критерий хи-квадрат с поправкой
- 82. 55. Коэффициент корреляции - всегда положительный; - всегда отрицательный; - по модулю больше 1; - определяет
- 83. 56. Корреляционная связь признаков прямая, если - признаки независимы; - признаки порядковые; - признаки качественные; -
- 84. 57. Корреляционная связь признаков обратная, если - с уменьшением значений одного признака, увеличиваются значения другого; -
- 85. 58. Корреляция сильная, если коэффициент корреляции - больше единицы; - меньше -1; - по модулю больше
- 86. 59. Корреляция слабая, если коэффициент корреляции - по модулю больше или равен 0,7; - близок к
- 87. 60. Линейная корреляция Пирсона применяется - для определения связи двух рядов количественных признаков с нормальным распределением;
- 88. 61. Ранговая корреляция Спирмена используется - для определения парной связи количественных признаков с нормальным распределением; -
- 89. 62. Критерий Мак-Нимара применяется: - для сравнения повторных измерений качественных признаков; - для сравнения качественных признаков
- 90. 63. Какие из приведенных данных о послеоперационном больном являются полными, а не цензурированными: - послеоперационный больной
- 91. 64. Что не требуется в анализе выживаемости? - чтобы все данные были полными, а не цензурируемыми;
- 92. 65. Что является невозможным исследованием при анализе выживаемости: - изучение продолжительности жизни (исход – смерть); -
- 93. 66. Биомедицинская статистика - не является необходимой областью знания для врача; - это инструмент для анализа
- 94. 67. «Температура больного» – относится к следующему типу переменной - количественная; - качественная; - порядковая; -
- 95. 68. Что такое «распределение признака»? - область возможных значений признака; - абсолютная или относительная частота встречаемости
- 96. 69. Медиана количественного признака - делит распределение пополам (половина значений признака меньше медианы, половина больше); -
- 97. 70. Распределение не является нормальным, если: - значение среднего обязательно близко к медиане (различие не более
- 98. 71. Медиана качественного признака - делит распределение пополам (половина значений признака меньше медианы, половина больше); -
- 99. 72. Для чего нужны описательные статистики? - для краткого описания большого массива количественных данных; - для
- 100. 73. Выборка является репрезентативной, если - она отражает свойства основной совокупности, то есть данные случайно (равновероятно)
- 101. 74. Что характеризует стандартное (среднеквадратичное) отклонение? - уровень значимости различия признаков; - разброс значений количественного признака
- 102. 75. Какие характеристики хорошо описывают ассиметричное распределение? - среднее и стандартное (среднеквадратичное) отклонение; - среднее и
- 103. 76. Как лучше сохранить результаты эксперимента (наблюдений): - в памяти; - в рукописном описании; - в
- 104. 77. Чем не является дисперсия? - средним квадратом отклонения от среднего арифметического количественного признака; - характеристикой
- 105. 78. Для чего в критерии хи-квадрат (при таблице сопряженности 2?2) применяется поправка на непрерывность (поправка Йейтса)?
- 106. 79. Нужно ли вычислять описательные статистики для качественных признаков? - обязательно, чтобы сжато описать выборку; -
- 107. 80. Как выбрать статистический критерий для решения конкретной задачи? - по типу признака и виду исследования;
- 108. 81. Чем близки различные статистические критерии? - имеют одинаковые формулы; - созданы одним и тем же
- 109. 82. Что выполняется раньше: проверка нормальности распределения количественного признака или критериальный анализ сравнения признаков в группах?
- 110. 83. Какой из критериев используется для проверки нормальности распределения? - Колмогорова-Смирнова; - линейной корреляции Пирсона; -
- 111. 84. Нулевая гипотеза - предполагает, что различия статистически значимы; - стандартизует один из признаков, присваивая ему
- 112. 85. Различия признака в сравниваемых группах статистически значимы, если - нулевая гипотеза отвергнута ошибочно; - вероятность
- 113. 86. Если корректно примененный критерий не нашел статистически значимых различий (р>0,05): - значит различий на самом
- 114. 87. Если чувствительность критерия низкая: - нужно попытаться увеличить объем выборки, проанализировать выбросы; - ничего не
- 115. 88. Если коэффициент корреляции близок к 1, но р>0,05, это означает: - связь между признаками сильная,
- 116. 89. Что такое «нижний квартиль»? - это медиана; - это 25-й персентиль: значение признака, которое делит
- 117. 90. Что такое «верхний квартиль»? - это 25-й персентиль; - это медиана; - это 75-й персентиль:
- 118. 91. Однофакторный дисперсионный анализ (ANOVA) - определяет значимость различия количественного признака с нормальным распределением в нескольких
- 119. 92. С помощью какого критерия можно сравнить вес исследуемых в четырех возрастных группах? - парный критерий
- 120. 93. Что важнее в статистическом анализе? - корректно применять статистические критерии; - знать формулы вычисления; -
- 121. 94. Что не требуется при описании материалов исследования? - описание гипотезы, подлежащей проверке; - описание данных
- 122. 95. Что не является уровнем значимости различия (р)? - ошибка первого рода; - вероятность ошибки отвергнуть
- 123. 96. Что такое ошибка первого рода? - вероятность найти различия там, где их на самом деле
- 124. 97. Что такое ошибка второго рода? - вероятность найти различия там, где их на самом деле
- 125. 98. Что такое двойное слепое исследование? - О том, какой препарат принимается, не знают ни пациенты,
- 126. 99. Проспективное исследование - исследование нерандомизированное; - исследователь пользуется имеющимися данными; - исследование слепое; - исследователь
- 127. 100. Продольные исследования - это одномоментные срезы для оценки распространенности определенного заболевания, факторов риска и т.д.;
- 128. 101. Применение статистических методов в медицине требует: - заучивания формул; - умения отыскать табличное значение; -
- 130. Скачать презентацию





















































































































 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»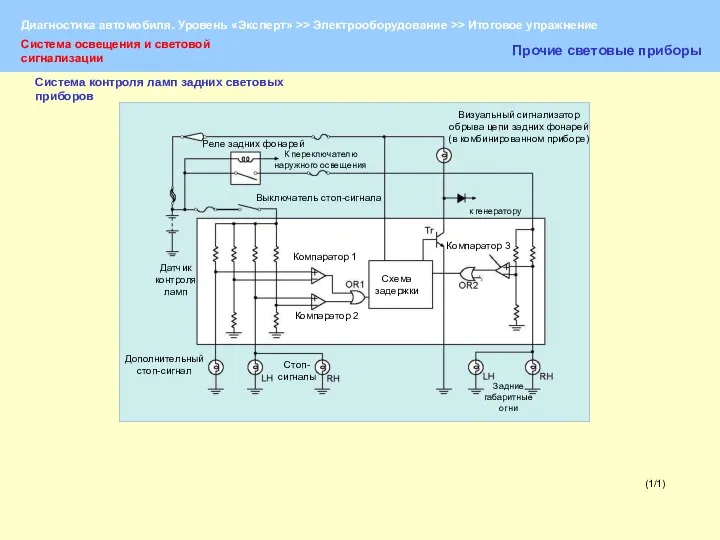 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс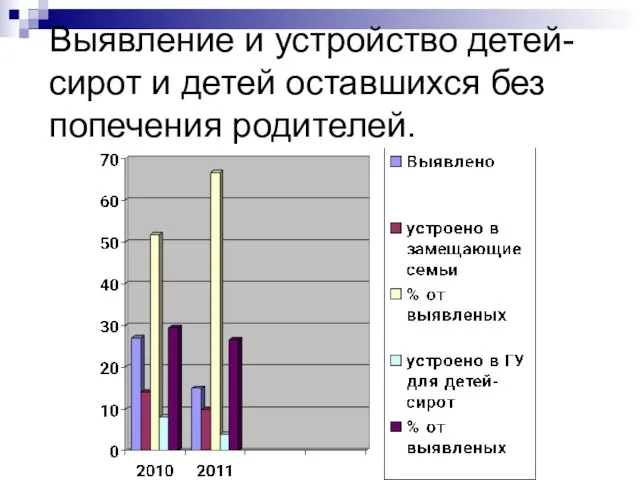 Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства