Степень числа 5 класс

Как найти степень числа.
Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 • 4 • 4 пишут 46 и произносят "четыре в шестой степени". 4 • 4 • 4 • 4 • 4 • 4 = 46

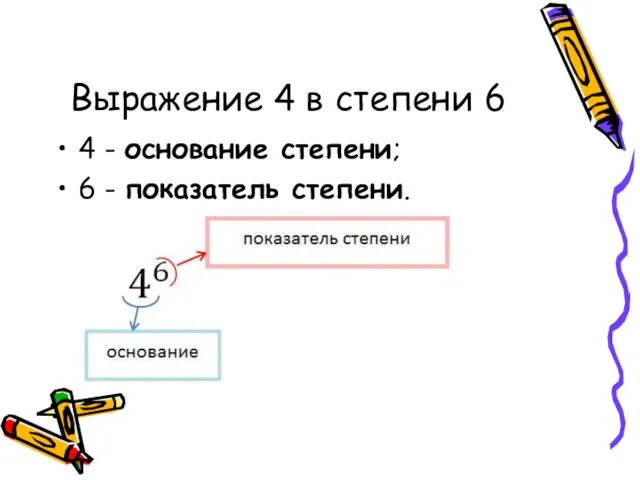
Выражение 4 в степени 6
4 - основание степени;
6 - показатель степени.

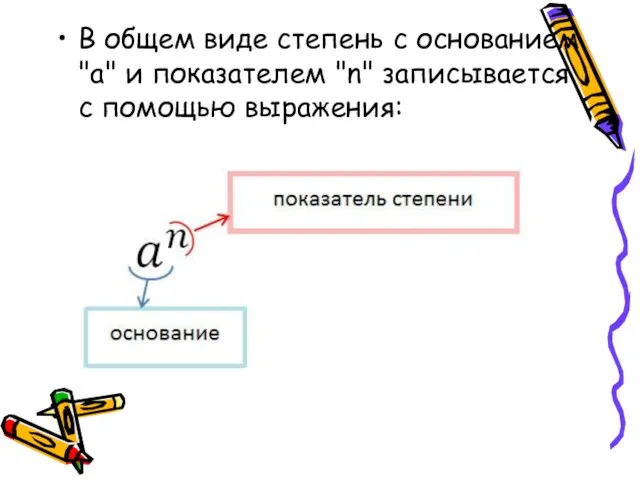
В общем виде степень с основанием "a" и показателем "n" записывается с помощью выражения:

Запомните!
Запись an читается так: "а в степени n" или "n-ая степень числа a".
Исключение составляют записи:
a2 - её можно произносить как "а в квадрате";
a3 - её можно произносить как "а в кубе".

Степенью числа "a" с натуральным показателем "n", бóльшим 1, называется произведение "n" одинаковых множителей, каждый из которых равен числу "a".

Конечно, выражения выше можно читать и по определению степени:
a2 - "а во второй степени";
a3 - "а в третьей степени".

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).
Степенью числа "а" с показателем n = 1 является само это число:
a1 = a
Любое число в нулевой степени равно единице.
a0 = 1
Ноль в любой натуральной степени равен нулю.
0n = 0
Единица в любой степени равна 1.
1n = 1

Выражение 00 (ноль в нулевой степени) считают лишённым смыслом.
(-32)ст0 = 1
0ст253 = 0
1ст4 = 1
При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.

При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.
Пример. Возвести в степень.
5ст3 = 5 • 5 • 5 = 125
2.5ст2 = 2.5 • 2.5 = 6.25

Возведение в степень отрицательного числа
5 класс

Запомните!
Основание степени (число, которое возводят в степень) может быть любым числом - положительным, отрицательным или нулём.

При возведении в степень положительного числа получается положительное число.
При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Запомните!
Отрицательное число, возведённое в чётную степень, есть число положительное.
Отрицательное число, возведённое в нечётную степень, - число отрицательное.
Квадрат любого числа есть положительное число или нуль, то есть:
a2 ≥ 0 при любом a.

Пример
2 • (- 3)ст2 = 2 • (- 3) • (- 3) = 2 • 9 = 18 - 5 • (- 2)ст3 = - 5 • (- 8) = 40

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (- 5)ст4 и -5ст4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (- 5)ст4 означает найти значение четвёртой степени отрицательного числа.
(- 5)ст4 = (- 5) • (- 5) • (- 5) • (- 5) = 625

В то время как найти -5ст4 означает, что пример нужно решать в 2 действия:
Возвести в четвёртую степень положительное число 5.
5ст4 = 5 • 5 • 5 • 5 = 625
Поставить перед полученным результатом знак "минус" (то есть выполнить действие вычитание).
-5ст4 = - 625

Обратите внимание!
Вычислить: - 6ст2 - (- 1)ст4
6ст2 = 6 • 6 = 36
-6ст2 = - 36
(- 1)ст4 = (- 1) • (- 1) • (- 1) • (- 1) = 1
- (- 1)ст4 = - 1
- 36 - 1 = - 37

Порядок действий в примерах со степенями.
5 класс

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Запомните!
В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Пример
Вычислить:

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней.