Стереометрия гуманитариямПрезентация курса

1-й урок: Что изучает стереометрия?
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «стереос» - объемный, пространственный и «метрео» - измерять.
Многие геометрические термины переведены с древнегреческого языка, т.к. геометрия зародилась в Древней Греции и развивалась в философских школах.

Одной из самых известных была пифагорейская школа, названная в честь основателя – Пифагора.
Символом этой школы был звездчатый пятиугольник – пентаграмма.
Пифагор
.

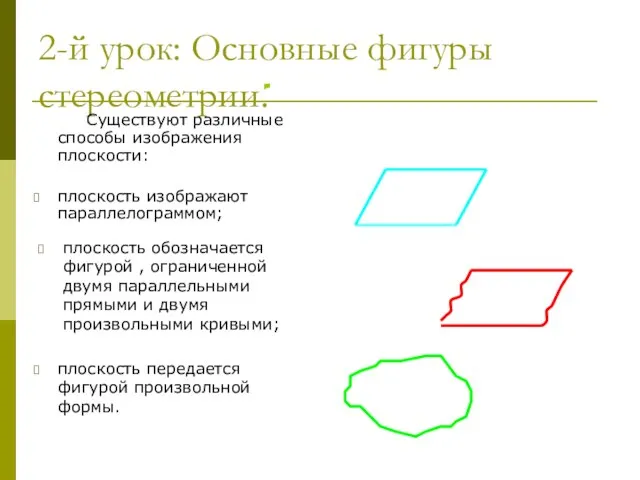
2-й урок: Основные фигуры стереометрии.
Существуют различные способы изображения плоскости:
плоскость изображают параллелограммом;
Назад
плоскость обозначается фигурой , ограниченной двумя параллельными прямыми и двумя произвольными кривыми;
плоскость передается фигурой произвольной формы.

3-й урок: Пространственные фигуры.
Урок посвящается подготовке к введению аксиом стереометрии.
Учащимся предлагаются следующие задачи:
Назад
Изобразите прямую а, лежащую на ней точку А и не лежащую на ней точку В.
Изобразите плоскость и две пересекающиеся прямые а и b , лежащие на ней.
Изобразите плоскость , лежащие на ней точки А и В, а также точки C и D, расположенные на разные стороны от плоскости.
Изобразите плоскость и пересекающую ее прямую а.
Изобразите плоскости, пересекающиеся под прямым углом.

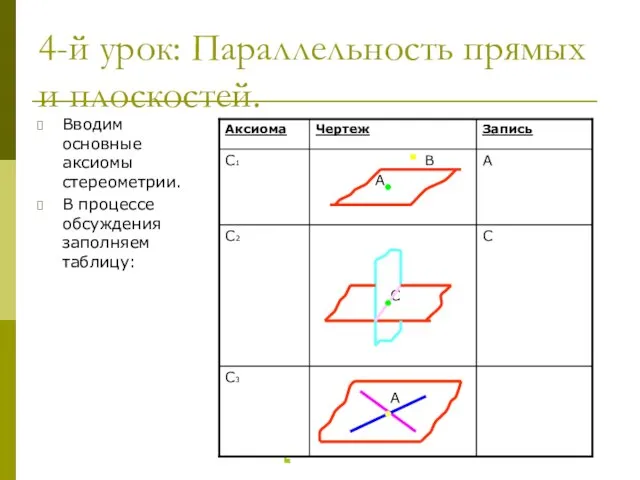
4-й урок: Параллельность прямых и плоскостей.
Вводим основные аксиомы стереометрии.
В процессе обсуждения заполняем таблицу:
Назад

5-й урок: Признаки параллельности плоскостей.
При изучении аксиом стереометрии вспоминаем первые аксиомы планиметрии и формулируем их пространственные аналогии.
В результате получаем следующую таблицу:
Назад

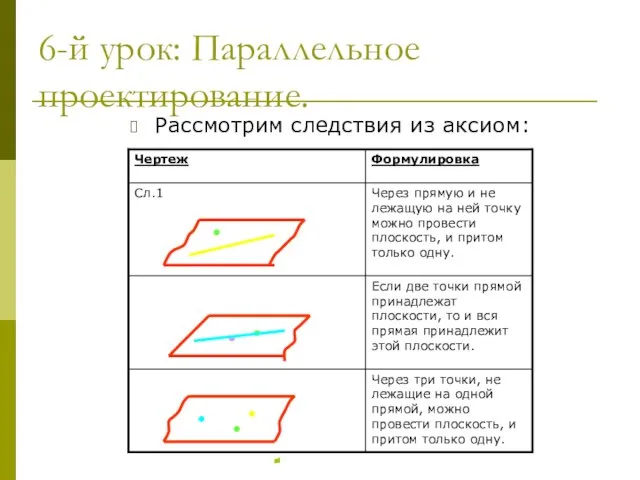
6-й урок: Параллельное проектирование.
Рассмотрим следствия из аксиом:
Назад

Изображение пространственных фигур на плоскости
На тему отводятся семь занятий:
Параллельное проектирование и его основные свойства;
Параллельное проектирование плоских фигур;
Изображение пространственных фигур в параллельной проекции;
Сечение многогранников;
Золотое сечение;
Центральное проектирование и его свойства;
Изображение пространственных фигур в центральной проекции.
Назад

Занятие 1: Параллельное проектирование и его основные свойства.
Основные свойства параллельного проектирования:
параллельной проекцией прямой является прямая или точка;
параллельной проекцией отрезка является отрезок или точка;
отношение длин отрезков, лежащих на одной прямой , сохраняется (в частности, середина отрезка при параллельном проектировании переходит в середину соответствующего отрезка);
параллельной проекцией двух параллельных прямых являются параллельные прямые, или одна прямая, или две точки;
отношение длин отрезков, лежащих на параллельных прямых, при параллельном проектировании сохраняется;
если фигура лежит в плоскости, параллельной плоскости проектирования, то ее параллельной проекцией на эту плоскость будет фигура, равная исходной.
Назад

Занятие 2: Параллельные проекции плоских фигур.
Рассматривается вопрос об изображении плоских фигур при параллельном проектировании.
Учащиеся должны представить себе, какие фигуры являются параллельными проекциями многоугольников и окружности.
Выяснить какие свойства многоугольников сохраняются при параллельном проектирования.
Узнать как строятся параллельные проекци основных плоских фигур.
Назад

Занятие 3: Изображение пространственных фигур в параллельной проекции.
На этом занятии учащиеся должны научиться правильно изображать основные пространственные фигуры, в том числе куб, прямоугольный параллелепипед, призму, цилиндр и конус.
Назад

Занятие 4: Сечение многогранников.
Это занятие является решающим для выработки у учащихся представлений о взаимном расположении прямых и плоскостей в пространстве.
Рассматриваются вопросы о построении сечений многогранников плоскостью.
Назад

Занятие 5: Золотое сечение.
При изображении пространственных фигур важное место занимает вопрос о нахождении наилучшего соотношения неравных частей, составляющих вместе единое целое.
Такое деление называют золотым сечением.

Золотое сечение в архитектуре
Известный русский архитекторы М. Казаков и В. Баженов широко использовали в своем творчестве “золотое сечение”.
Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Первой клинической
Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова.
Сенат
Дом Пашкова
Назад

Занятие 6: Центральное проектирование и его свойства.
Назад
Вначале рассматривается определение центрального проектирования.
Рассматриваются различные случаи центрального проектирования.

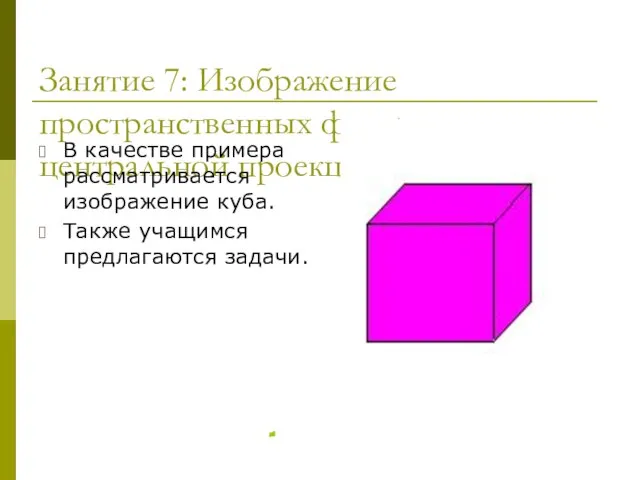
Занятие 7: Изображение пространственных фигур в центральной проекции.
В качестве примера рассматривается изображение куба.
Также учащимся предлагаются задачи.
Назад

Многогранники.
В этот курс включены следующие занятия:
Правильные многогранники.
Полуправильные многогранники.
Звездчатые многогранники.
Теорема Эйлера.
Назад

Занятие 1: Правильные многогранники.
В начале урока вводится определение выпуклого многогранника: «Выпуклым называется многогранник, если он расположен по одну сторону от плоскости каждой его грани».
Рассматриваются модели выпуклых многогранников.

Пирамида
составлена из n-угольников и n треугольников

Призма
составлена из двух равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов

Икосаэдр
составлен из двадцати равносторонних треугольников

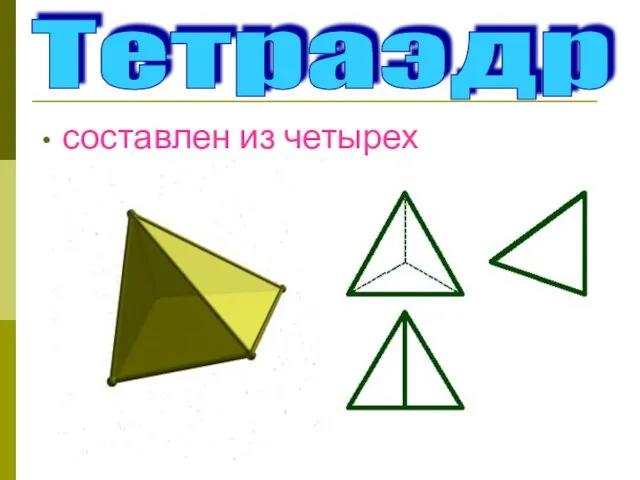
Тетраэдр
составлен из четырех треугольников

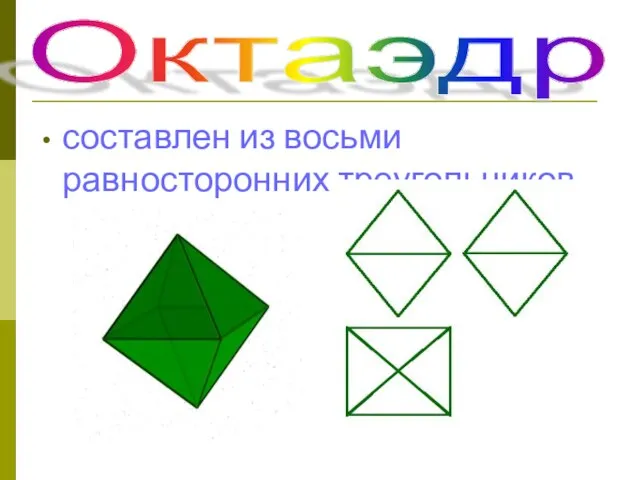
Октаэдр
составлен из восьми равносторонних треугольников

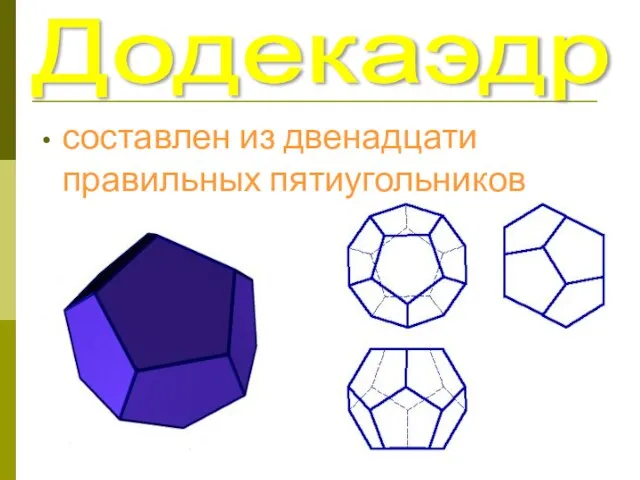
Додекаэдр
составлен из двенадцати правильных пятиугольников

Гексаэдр
составлен из шести квадратов, также называется КУБ
Назад

Занятие 2: Полуправильные многогранники.
Вводится определение полуправильного многогранника.
Демонстрируются модели.
Назад

Занятие 3: Звездчатые многогранники.
Рассматриваются правильные звездчатые многогранники.
Назад

Занятие 4: Теорема Эйлера.
Одно из наиболее интересных свойств выпуклых многогранников описано теоремой Эйлера.
Назад
Сначала с учащимися рассматриваются известные им многогранники и заполняется таблица.
Затем выводится и сама теорема: В-Р+Г=2

Углы между прямыми и плоскостями в пространстве.
При изучении данной темы желательно отметить, что проблема измерения углов восходит к глубокой древности.
Следует как можно шире осветить историю создания измерительных приборов и методы измерения.
Для это предлагается провести следующие занятия:
Объем фигур в пространстве. Объем цилиндра;
Принцип Кавальери;
Объем конуса;
Объем шара.
Назад

Занятие 1: Объем фигур в пространстве. Объем цилиндра.
На этом занятии рассматриваются проблемы измерения объемов пространственных фигур.
Перечисляются основные свойства объема:
объем фигуры в пространстве является неотрицательным числом;
объем куба с ребром 1 равен 1;
равные фигуры имеют равные объемы;
если фигура Ф составлена из фигур Ф1 и Ф2, то объем фигуры Ф равен сумме объемов фигур Ф1 и Ф2.
Назад

Занятие 2:
Принцип Кавальери.
Дается формулировка принципа Кавальери.
Применяя данный принцип решаем задачи.
Назад

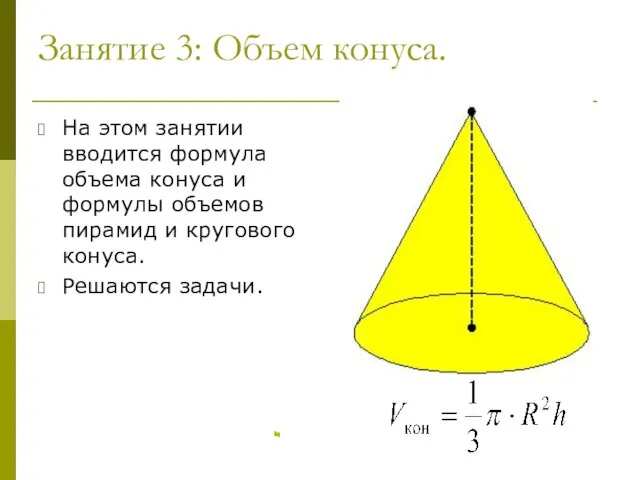
Занятие 3: Объем конуса.
На этом занятии вводится формула объема конуса и формулы объемов пирамид и кругового конуса.
Решаются задачи.
Назад

Занятие 4: Объем шара.
На занятии выводится формула объема шара:
Решаются задачи по данной теме.
Назад

Занятие 1: Определение и простейшие примеры фигур вращения.
Дается определение фигуры вращения, а также понятие поворота в пространстве относительно прямой.
Рассматриваются задачи по данной теме.
Учащимся предлагаются задачи для самостоятельной работы.
Назад