Содержание
- 2. «Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но
- 3. Тренировочная работа №1 Расстояние от точки до прямой С2
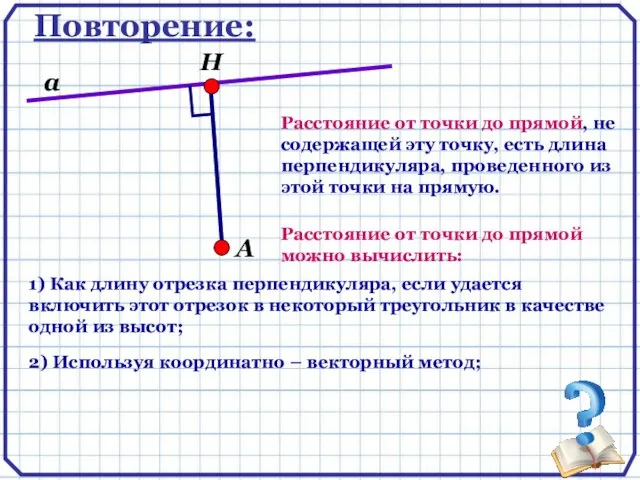
- 4. Повторение: А Н а Расстояние от точки до прямой, не содержащей эту точку, есть длина перпендикуляра,
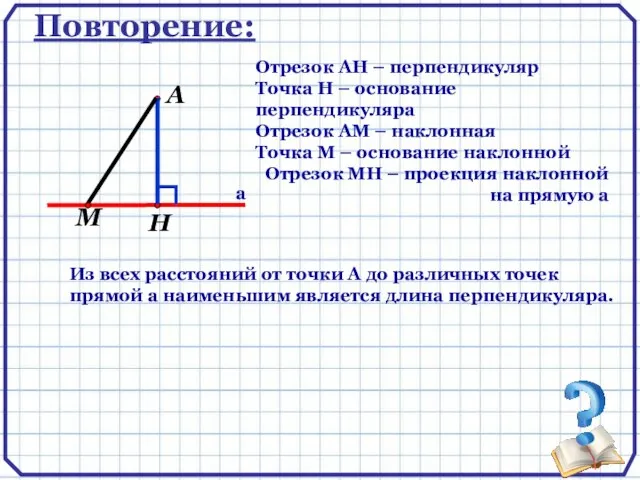
- 5. А а Повторение: Отрезок АН – перпендикуляр Точка Н – основание перпендикуляра Отрезок АМ – наклонная
- 6. В единичном кубе АВСДА1В1С1Д1 найдите расстояние от точки А до прямой ВД1. № 1 1 1
- 7. Критерии оценивания выполнения задания С2
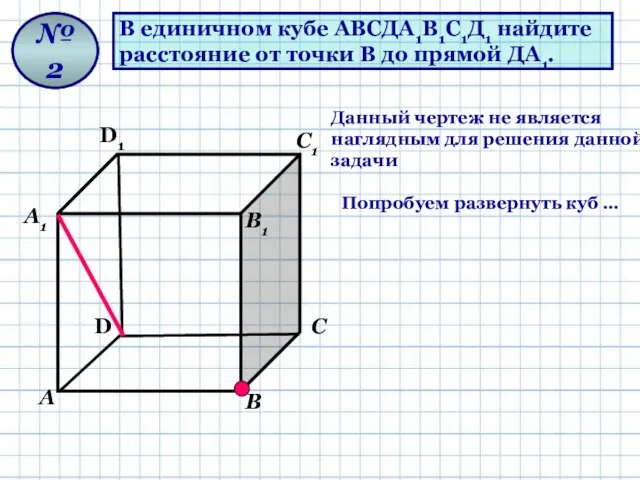
- 8. В единичном кубе АВСДА1В1С1Д1 найдите расстояние от точки В до прямой ДА1. № 2 Данный чертеж
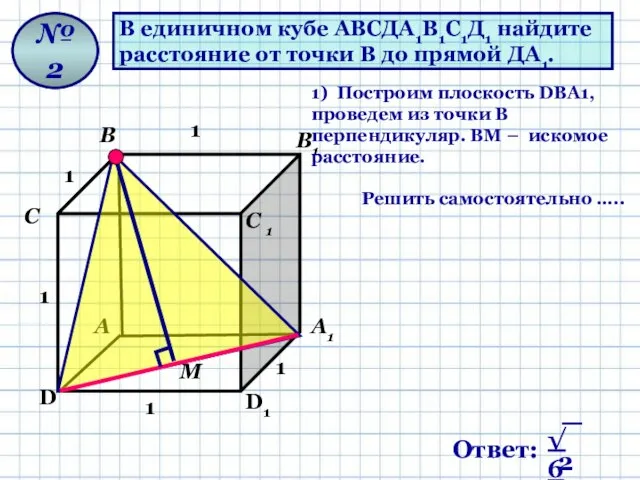
- 9. В единичном кубе АВСДА1В1С1Д1 найдите расстояние от точки В до прямой ДА1. № 2 1) Построим
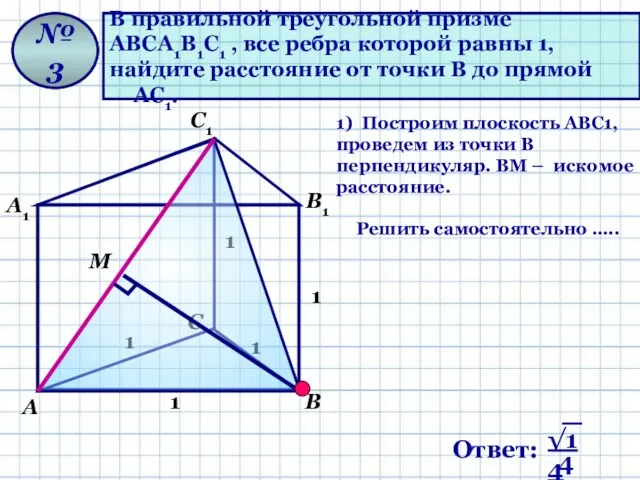
- 10. В правильной треугольной призме АВСА1В1С1 , все ребра которой равны 1, найдите расстояние от точки В
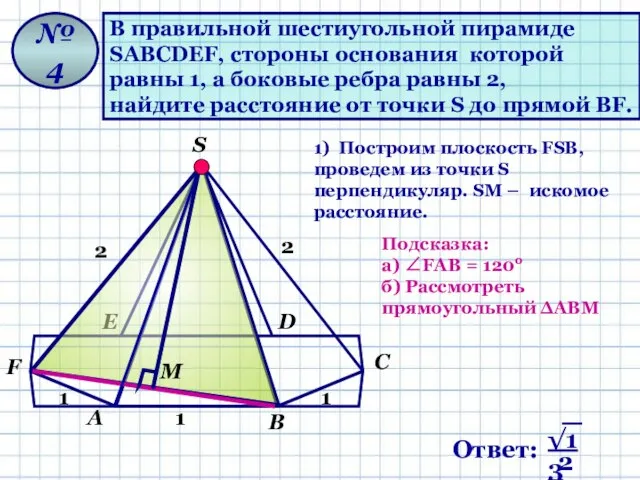
- 11. В правильной шестиугольной пирамиде SАВСDЕF, стороны основания которой равны 1, а боковые ребра равны 2, найдите
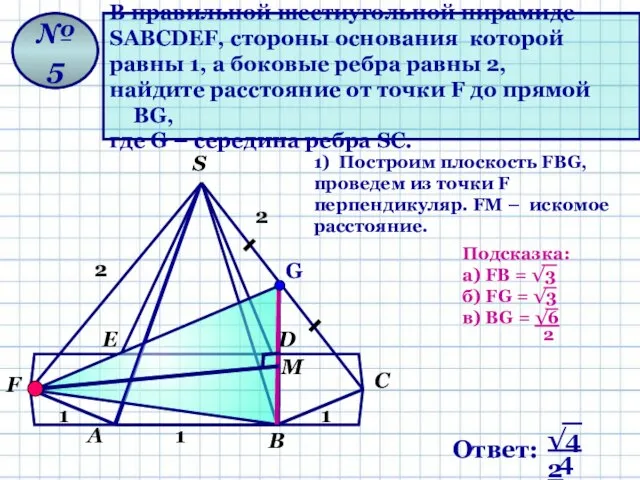
- 12. В правильной шестиугольной пирамиде SАВСDЕF, стороны основания которой равны 1, а боковые ребра равны 2, найдите
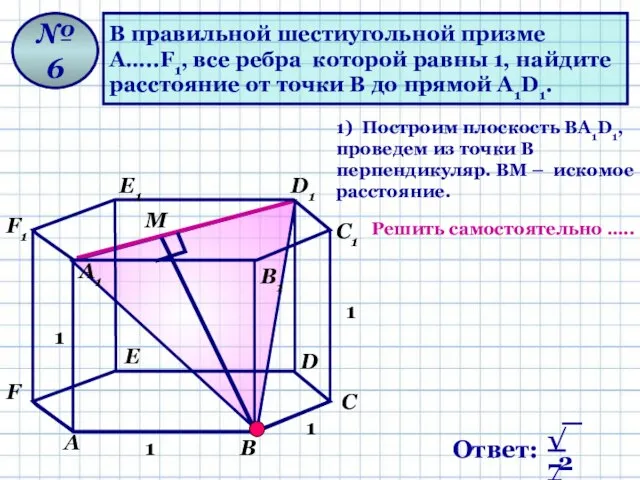
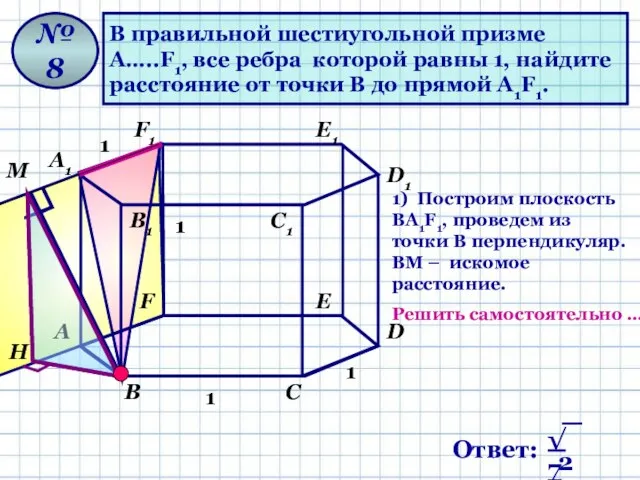
- 13. В правильной шестиугольной призме А…..F1, все ребра которой равны 1, найдите расстояние от точки В до
- 14. В правильной шестиугольной призме А…..F1, все ребра которой равны 1, найдите расстояние от точки А до
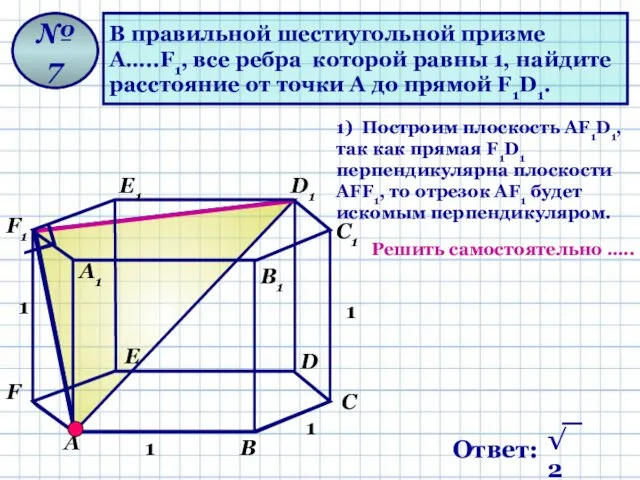
- 15. В правильной шестиугольной призме А…..F1, все ребра которой равны 1, найдите расстояние от точки В до
- 16. В единичном кубе АВСДА1В1С1Д1 найдите расстояние от точки А до прямой: а) В1Д1; б) А1С Домашнее
- 18. Скачать презентацию





 Система подготовки к ЕНТ по биологии.
Система подготовки к ЕНТ по биологии. 36f368566b7b47859a7e1559c9c90b96 (1)
36f368566b7b47859a7e1559c9c90b96 (1) С Рождеством
С Рождеством Обзорная экскурсия по музею
Обзорная экскурсия по музею Автограф
Автограф Кому на Руси жить хорошо
Кому на Руси жить хорошо Напольный табачный диспенсер
Напольный табачный диспенсер Живая природа Алтая. Фотовыставка
Живая природа Алтая. Фотовыставка Интерактивная доска в обучении
Интерактивная доска в обучении Воспаление, общие вопросы. Экссудативное воспаление
Воспаление, общие вопросы. Экссудативное воспаление Масленица
Масленица Строение вещества. Повторение и обобщение темы
Строение вещества. Повторение и обобщение темы Вовлечение несовершеннолетних в совершение преступления
Вовлечение несовершеннолетних в совершение преступления Курс_Кристина_2022_мастерская_общий_день_rus_1
Курс_Кристина_2022_мастерская_общий_день_rus_1 Земноводные (2 класс)
Земноводные (2 класс) Создание робота
Создание робота Емельян Иванович Пугачев
Емельян Иванович Пугачев 7 чудес древнего мира
7 чудес древнего мира Европейская медиагруппа (ЕМГ). Сравнительный анализ
Европейская медиагруппа (ЕМГ). Сравнительный анализ Исследование и разработка направленного ответвителя с улучшенными характеристиками
Исследование и разработка направленного ответвителя с улучшенными характеристиками «Электричество и растения».
«Электричество и растения». Итоги аттестации 9-ых классов2011 – 2012 учебный год
Итоги аттестации 9-ых классов2011 – 2012 учебный год Презентация на тему Народные движения
Презентация на тему Народные движения  О чем может рассказать капелька
О чем может рассказать капелька Крыши и кровли зданий малой и средней этажности
Крыши и кровли зданий малой и средней этажности ПРЕДСТАВЛЕНИЕ О БАЗАХ ДАННЫХ
ПРЕДСТАВЛЕНИЕ О БАЗАХ ДАННЫХ Автоматизация [р] в начале слова
Автоматизация [р] в начале слова Золотое правило нравственности
Золотое правило нравственности