Свойства функций (9 класс)

Вступительное слово.
Дорогие друзья! Мы представляем Вашему вниманию презентацию для обучения и подготовке к экзамену по алгебре. Тема нашей работы «Свойства функций». В работе представлены те функции, которые изучаются в курсе алгебры 7, 8, 9 классов. Получить дополнительную информацию вы можете по ссылке>>
Желаем успехов.

Выберите тему:

Свойства функций

Примеры построения

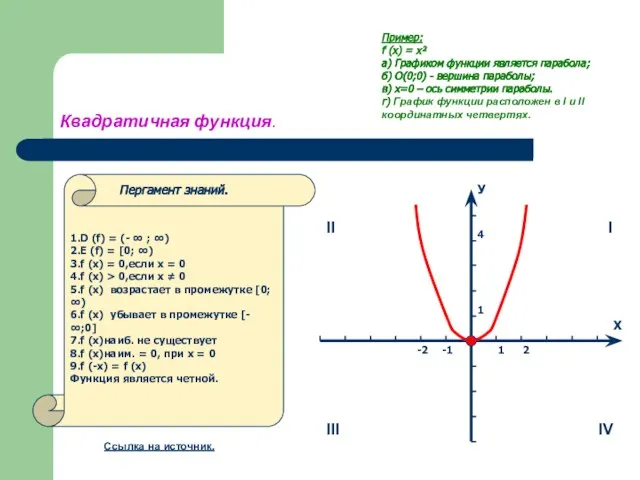
Квадратичная функция.
У
Х
-2
-1
1
2
1
4
Пример:
f (x) = х²
а) Графиком функции является парабола;
б) О(0;0) - вершина параболы;
в) х=0 – ось симметрии параболы.
г) График функции расположен в I и II координатных четвертях.
1.D (f) = (- ∞ ; ∞)
2.E (f) = [0; ∞)
3.f (x) = 0,если х = 0
4.f (х) > 0,если х ≠ 0
5.f (x) возрастает в промежутке [0; ∞)
6.f (x) убывает в промежутке [- ∞;0]
7.f (x)наиб. не существует
8.f (x)наим. = 0, при х = 0
9.f (-x) = f (x)
Функция является четной.
Пергамент знаний.
Ссылка на источник.
IV
II
I
III

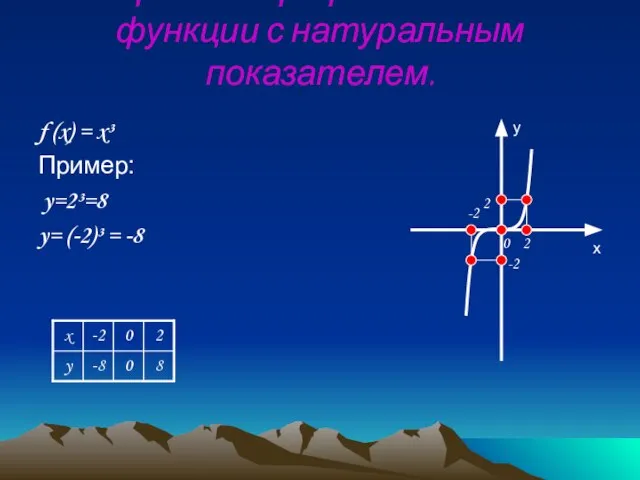
Степенная функция с натуральным показателем.
Пример:
f (x) = x³.
а)Графиком функции является кубическая парабола
б)График функции проходит через точку (0;0)
в)График функции расположен в I и III координатных четвертях.
1.D (f) = (- ∞ ; ∞)
2.E (f) = ( - ∞ ; ∞)
3.f (x) = 0, при х = 0
4.f (x) > 0, если x > 0
5.f (x) < 0, если х < 0
6.f (x) возрастает в промежутке (- ∞; ∞)
7.f (х)наиб. не сущ.
8.f (х)наим. не сущ.
9.f (-x) = - f (x)
Функция является нечетной.
Пергамент знаний.
У
Х
-1
1
1
-1
Ссылка на источник.
II
I
III
IV

Линейная функция.
1.D (f) = (- ∞;∞)
2.E (f) = ( - ∞;∞)
3.f (x) = 0 ,при x= -0.5
4.f (x) > 0, если x > -0,5
5.f (x) < 0, если x < -0,5
6.f (x) возрастает на всей области определения
8.f (x)наиб. не сущ.
9.f (x)наим. не сущ.
10.Функция не является ни четной, ни нечетной.
Пергамент знаний.
Ссылка на источник.
У
Х
Пример:
f (x)= 2x + 1
а) Графиком функции является прямая,
б)График функции проходит через точки (-0,5;0) и (0;1)
-0.5
1
II
I
III
IV

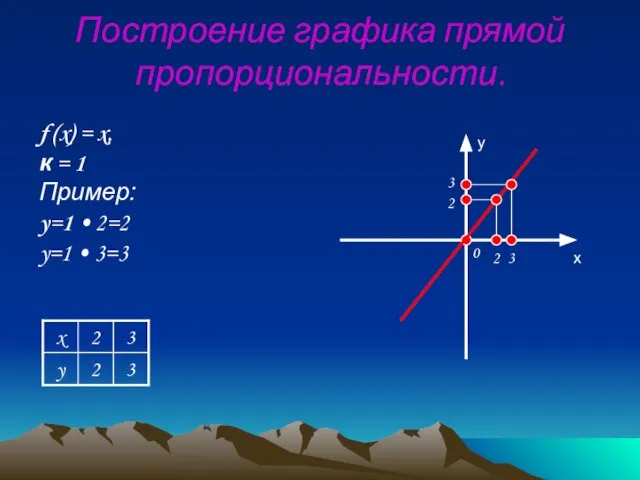
Прямая пропорциональность.
Пример:
f (x) = kx, k>0
а)Графиком функции является прямая;
б)График функции проходит через точку (0;0)
в)График функции расположен в I и III координатных четвертях.
1.D (f) = (- ∞; ∞)
2.Е (f) = ( - ∞; ∞)
3.f (x) = 0, при х = 0
4.f (x) > 0, при x > 0
5.f (x) < 0, при x < 0
6.f (x) возрастает в промежутке
(- ∞; ∞), т.е. на всей числовой прямой.
7.f (x)наиб.- не сущ.
8.f (x)наим.- не сущ.
9.f (-x) = - f (x)
Функция является нечетной.
Пергамент знаний.
Ссылка на источник.
III
IV
II
I
У
Х

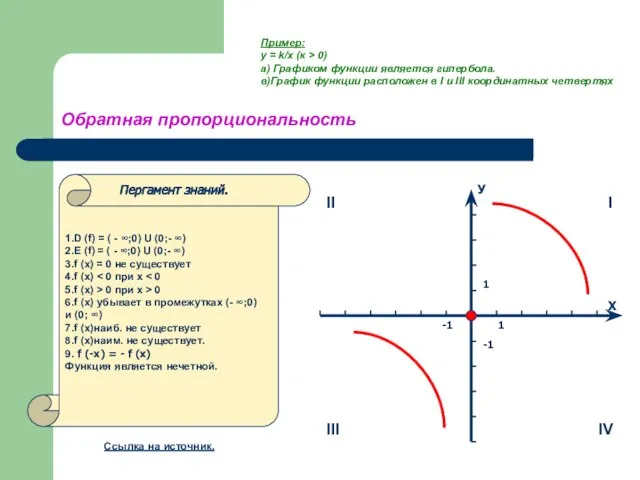
Обратная пропорциональность
1.D (f) = ( - ∞;0) U (0;- ∞)
2.E (f) = ( - ∞;0) U (0;- ∞)
3.f (x) = 0 не существует
4.f (x) < 0 при х < 0
5.f (x) > 0 при x > 0
6.f (x) убывает в промежутках (- ∞;0)
и (0; ∞)
7.f (x)наиб. не существует
8.f (x)наим. не существует.
9. f (-x) = - f (x)
Функция является нечетной.
Пергамент знаний.
Ссылка на источник.
Пример:
y = k/x (к > 0)
а) Графиком функции является гипербола.
в)График функции расположен в I и III координатных четвертях
У
Х
II
III
I
IV
1
-1
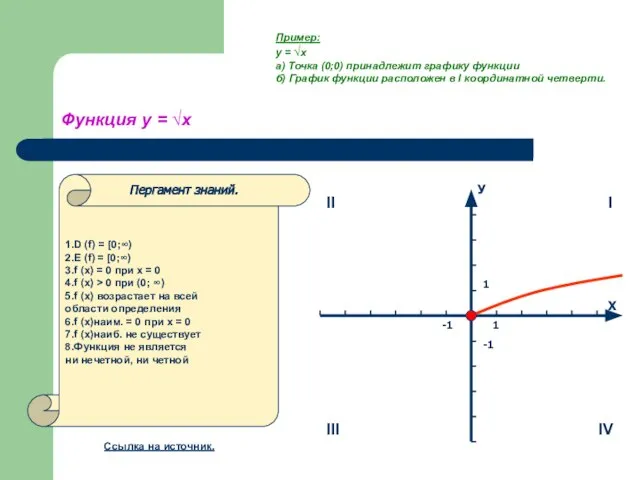
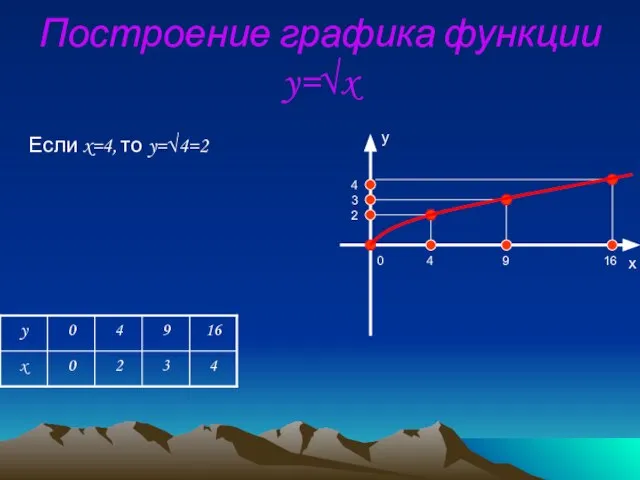
1
-1

Функция у = √х
1.D (f) = [0;∞)
2.E (f) = [0;∞)
3.f (x) = 0 при x = 0
4.f (x) > 0 при (0; ∞)
5.f (x) возрастает на всей
области определения
6.f (x)наим. = 0 при х = 0
7.f (x)наиб. не существует
8.Функция не является
ни нечетной, ни четной
Пергамент знаний.
Ссылка на источник.
Пример:
y = √x
а) Точка (0;0) принадлежит графику функции
б) График функции расположен в I координатной четверти.
У
Х
II
I
III
IV
1
-1
1
-1

Пример построения графика квадратичной функции.
F(x)= 2x² + 8x +2
1) Ветви 2) х = -8 ∕ 2•2= -2
y = f(x ) = 2•(-2)² + 8•(-2)+2= -6
С (-2;-6)
3) х=-2 ( ось симметрии параболы)
4)
у
х
-2
-6

Пример построения графика линейной функции
y
x
1
2
0
5
Пример: y=2x+1
Если x=0, то y=2 • 0+1=1
Если x=2, то y=2•2+1=5

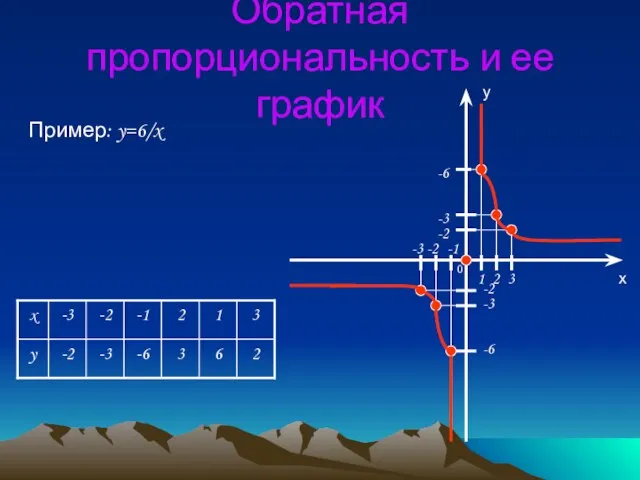
Обратная пропорциональность и ее график
Пример: y=6/x
-2
-3
-6
-1
-2
-3
-6
-2
-3
1
2
3
y
x
0

4
9
16
2
3
4
0
Если x=4, то y=√4=2
Построение графика функции y=√x
y
x

Построение графика прямой пропорциональности.
f (x) = x,
к = 1
Пример:
y=1 • 2=2
y=1 • 3=3
y
x
0
2
3
3
2

Построение графика степенной функции с натуральным показателем.
f (x) = x³
Пример:
y=2³=8
y= (-2)³ = -8
y
x
0
2
2
-2
-2

авторы:
Ю.Н. Макарычев
Н.Г. Миндюк
К.И. Нешков
С.Б. Суворова
год издания: 2005
Издательство: Просвещение.
Кликните на картинку, что бы перейти на Интернет ресурс, по учебнику.