Текстовая задача и процесс её решения

Почему решению текстовых задач в начальном курсе обучения математике уделяется огромное внимание?
Текстовые задачи являются
средство формирования многих математических понятий
средством формирования умений строить математические модели реальных явлений
средство развития мышления, интуиции, смекалки

Программные требования
Работа с текстовыми задачами
Решение текстовых задач арифметическим способом. Задачи, содержащие отношения «больше (меньше) на…», «больше (меньше) в…». Зависимости между величинами, характеризующими процессы движения, работы, купли‑продажи и др. Скорость, время, путь; объём работы, время, производительность труда; количество товара, его цена и стоимость и др. Планирование хода решения задачи. Представление текста задачи (схема, таблица, диаграмма и другие модели).
Задачи на нахождение доли целого и целого по его доле.

Текстовая задача - описание на естественном языке ситуации или процесса с требованием дать количественную характеристику какого-либо компонента этого явления, установить наличие и отсутствие некоторого отношения между компонентами или определить вид этого отношения

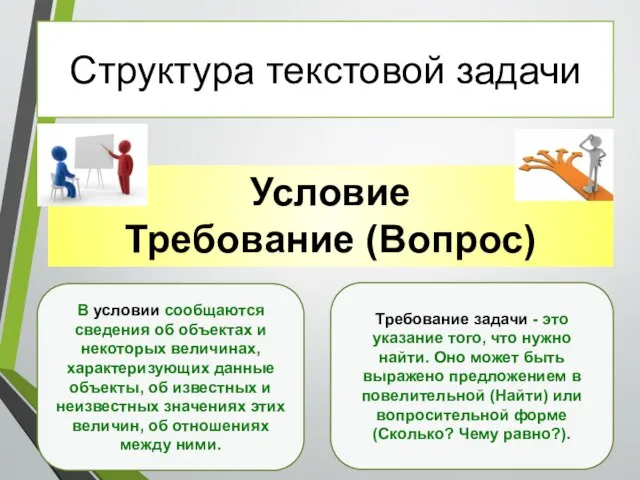
Условие
Требование (Вопрос)
Структура текстовой задачи
Требование задачи - это указание того, что нужно найти. Оно может быть выражено предложением в повелительной (Найти) или вопросительной форме (Сколько? Чему равно?).
В условии сообщаются сведения об объектах и некоторых величинах, характеризующих данные объекты, об известных и неизвестных значениях этих величин, об отношениях между ними.

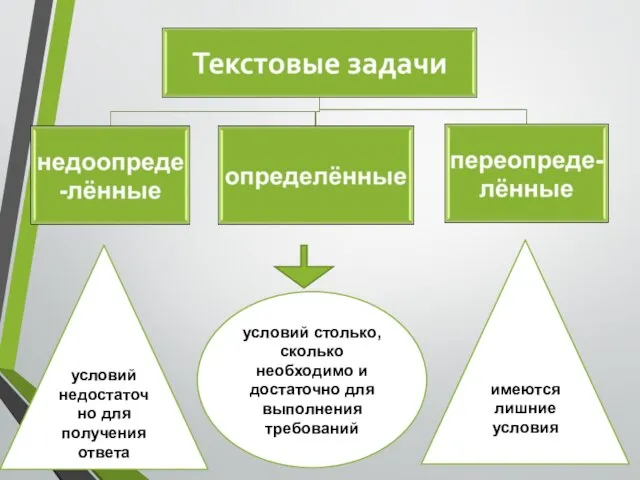
условий недостаточно для получения ответа
условий столько, сколько необходимо и достаточно для выполнения требований
имеются лишние условия

Арифметический
найти ответ на требование задачи посредством выполнения арифметических действий над числами
Алгебраический
найти ответ на требование задачи необходимо составив и решив уравнение или систему уравнений
Одну и ту же задачу можно решить различными арифметическими или алгебраическими способами

Задача 1. Сшили 3 платья, расходуя на каждое по 4 метра ткани. Сколько блуз можно сшить из этой ткани, если расходовать на одну блузку 2 м?
1способ:
1) 4∙3=12 (м)- столько было ткани;
2) 12:2=6 (б) – можно сшить из 12 метров ткани
2 способ:
1) 4:2=2 (раза) – во столько раз больше идет ткани на платье, чем на блузку;
2) 3∙2=6 (б) – столько блуз можно сшить.
Арифметический метод решения задачи

Пусть кафтан стоил x руб. Тогда хозяин заплатил работнику за 7 месяцев: (x + 5) руб
А если бы работник отработал год, то получал бы в месяц: ((x + 12):12) руб.
=> за 7 месяцев он бы заработал: (7 · (x + 12):12) руб.
Используя эти данные составим уравнение:
7 · (x + 12):12 = x + 5
Дорешайте задачу самостоятельно и сверьте ответы.
Решение задачи алгебраическим методом

Этапы решения задачи и приёмы их выполнения
1.Восприятие и анализ задачи.
2.Поиск плана решения задачи.
3.Осуществление плана решения
задачи.
4.Проверка решения задачи.

1 этап – восприятие
и анализ содержания задачи
Цель этапа:
Понять ситуацию, описанную в задаче, выделить условия и требования, назвать известные и искомые объекты, выделить все отношения (зависимости) между ними.

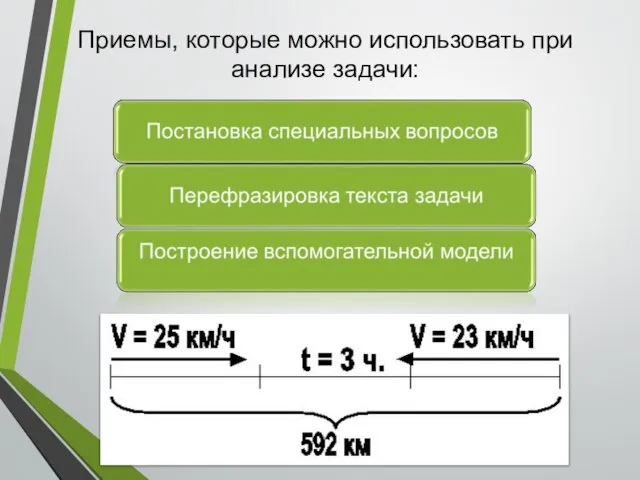
Приемы, которые можно использовать при анализе задачи:

Чтобы разобраться в содержании задачи, вычленить условия и требования, нужно задать специальные вопросы:
О чём задача?
Что требуется найти в задаче?
Что обозначают те или иные слова в тексте задачи?
Что в задаче неизвестно?
Что является искомым?

Разбор задачи по тексту или по ее вспомогательной модели
2 этап - поиск и составление плана решения задачи
На поезде, который шел со скоростью 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем проехал. Каков весь путь туриста?
Рассуждения ведем от данных к вопросу:
известно, что 6 ч турист проехал на поезде, который шел со скоростью 56 км/ч; по этим данным можно узнать расстояние, которое проехал турист за 6 ч, - для этого достаточно скорость умножить на время.
Зная пройденную часть расстояния и то, что оставшееся расстояние нужно умножить на 4 (увеличить в 4 раза).
Зная, сколько километров турист проехал и сколько ему осталось ехать, можем найти весь путь, выполнив сложение найденных отрезков пути. Итак, первым действием будем находить расстояние, которое турист проехал на поезде; вторым действием – расстояние, которое ему осталось проехать; третьим – весь путь.

На поезде, скорость которого 56 км/ч, турист проехал 6 ч. После этого ему осталось проехать в 4 раза больше, чем он проехал. Каков весь путь туриста?
3 этап – осуществление плана решения задачи
Запись решения по действиям с пояснением к каждому выполненному действию.
56 ∙ 6=336 (км) – турист проехал за 6 ч.
336 ∙ 4=1344(км) – осталось проехать туристу.
336+1344=1680(км) – должен был проехать турист.
Если пояснения даются в устной форме (или совсем не даются), то запись будет следующей:
56 ∙ 6=336 (км)
336 ∙ 4=1344 (км)
336+1344=1680 (км)

Запись решения по действиям с вопросами:
1)Сколько километров проехал турист на поезде?
56 ∙ 6=336(км)
2) Сколько километров осталось проехать туристу?
336 ∙ 4=1344(км)
3) Сколько километров турист должен был проехать?
336+1344=1680(км)
Запись решения в виде выражения:
56 ∙ 6 (км) – расстояние, которое проехал турист на поезде за 6ч
56 ∙ 6 ∙ 4(км) – расстояние, которое осталось проехать туристу
56 ∙ 6 + 56 ∙ 6 ∙ 4 (км) – путь, который должен проехать турист
56 ∙ 6 + 56 ∙ 6 ∙ 4=1680 (км)
Пояснения к действиям можно не записывать, а давать их в устной форме.
Тогда запись решения задачи примет вид:
56 ∙ 6 + 56 ∙ 6 ∙ 4=1680 (км)

Приёмы проверки
1. Соотнесение полученного результата с условием задачи.
2.Решение задачи другим способом.
3. Прикидка.