ТЕМА 1.4

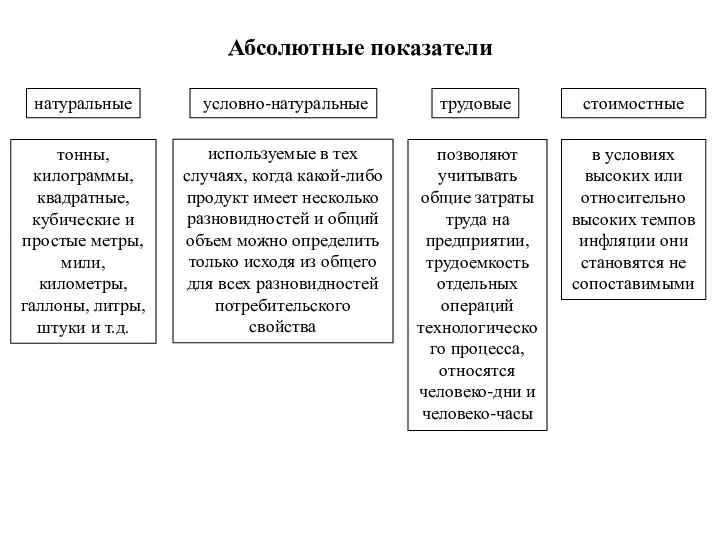
Абсолютные показатели

Относительные показатели

Относительный показатель динамики
Относительный показатель плана
состояние на данный момент времени к уровню этого же процесса или явления в прошлом
характеризует во сколько раз, планируемый объемный показатель превысит достигнутый уровень или сколько процентов от этого уровня составит

Относительный показатель реализации плана
отражает фактический объем производства или реализации в процентах или коэффициентах по сравнению с плановым уровнем
Относительный показатель структуры
соотношение структурных частей изучаемого объекта и их целого

Относительный показатель координации
отношение одной части совокупности к другой части этой же совокупности
Относительный показатель интенсивности
характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды, например уровень безработицы

Относительный показатель сравнения
соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.)

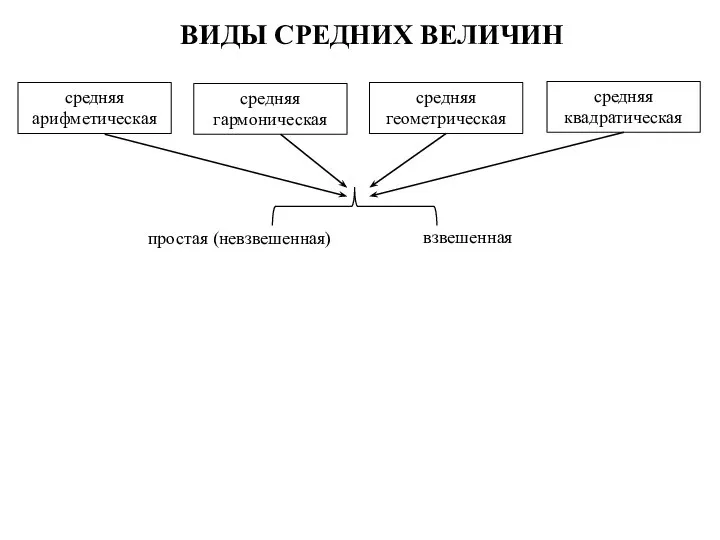
ВИДЫ СРЕДНИХ ВЕЛИЧИН

Средняя арифметическая
где хi – вариант, а n – количество единиц совокупности
Простая
Взвешенная
где хi – вариант, а fi – частота или статистический вес.

Средняя гармоническая
Простая
Взвешенная
Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.

Средняя геометрическая
Простая
Взвешенная
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста
где хi – цепной коэффициент роста уровня ряда динамики; n – число цепных коэффициентов роста в ряду динамики
где хi – значение варьирующего признака i-го элемента; fi – вес признака (частота повторения признака)

Средняя квадратическая
Простая
Взвешенная
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой.
Для сгруппированных данных используют формулу средней квадратической взвешенной.
где n — число единиц совокупности или число вариантов; х — значения варьирующегося признака
где fi – частота ряда распределения или удельный вес в совокупности

ПРАВИЛО
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.

Структурные средние
величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.
МОДА
МЕДИАНА
значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы

Мода
Для интервального ряда мода
где хо – начальная (нижняя) граница модального интервала;
h – величина интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующая модальному;
fМо+1– частота интервала следующая за модальным.
В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту