Тема: «Линейная функция».

Немного истории.
17 век. В связи с развитием механики в математику проникают идеи функциональной зависимости одной переменной величины от другой. Термин «функция» означает совершение, исполнение (от латинского слова)
19 век.
Русский математик Н.И.Лобачевский развил определение понятия функции.
Немецкий математик Л.Дирихле дал определение понятия функции очень близкое к тому, которым пользуются сегодня.
Учебник стр. 53

Машина выезжает из гаража (пункт C).
Проехав 30 км (СB=30км),остановилась у переезда(пункт B). После остановки она продолжает движение по шоссе с постоянной скоростью 50 км/ч до пункта A.
t (в часах) -время движения машины от B до A
S1 (в километрах) - путь BA
S1= 50t
S2 (в километрах)- путь CA
S2 =50t+30
Примечание.
Зависимость пути от времени задается формулами.
t – независимая переменная,
S – зависимая переменная
(функция)
y=kx
y=kx+b
C
B

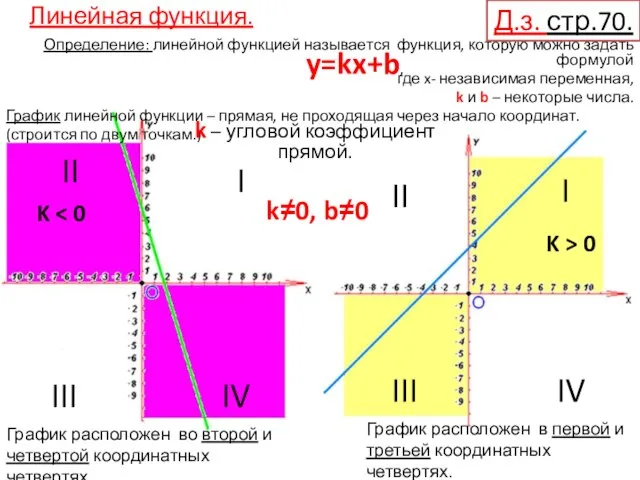
Линейная функция.
Определение: линейной функцией называется функция, которую можно задать формулой
где x- независимая переменная,
k и b – некоторые числа.
График линейной функции – прямая, не проходящая через начало координат.
(строится по двум точкам.)
I
II
III
IV
k – угловой коэффициент прямой.
K < 0
K > 0
График расположен в первой и третьей координатных четвертях.
График расположен во второй и четвертой координатных четвертях.
I
II
III
IV
k≠0, b≠0
y=kx+b,
Д.з. стр.70.

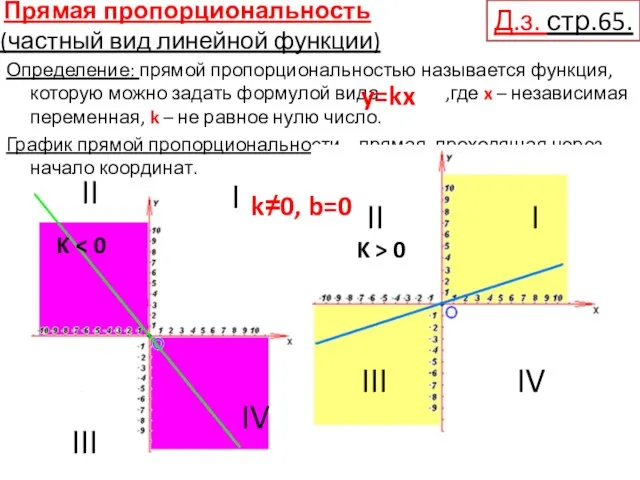
Прямая пропорциональность
(частный вид линейной функции)
Определение: прямой пропорциональностью называется функция, которую можно задать формулой вида ,где x – независимая переменная, k – не равное нулю число.
График прямой пропорциональности – прямая, проходящая через начало координат.
I
II
III
IV
K < 0
I
II
III
IV
K > 0
k≠0, b=0
y=kx
Д.з. стр.65.

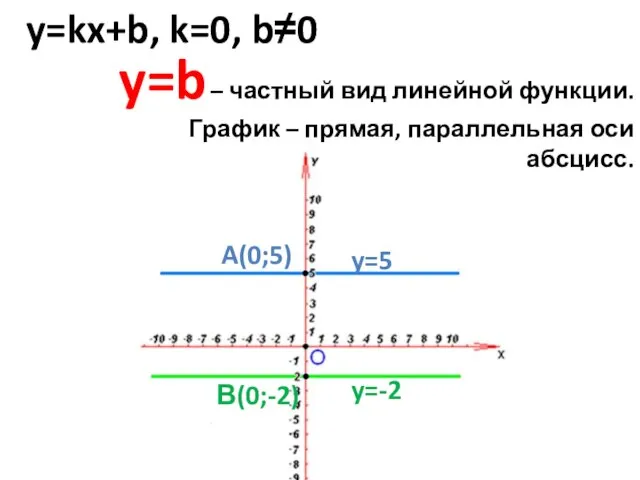
y=kx+b, k=0, b≠0
y=5
y=-2
A(0;5)
В(0;-2)
y=b – частный вид линейной функции.
График – прямая, параллельная оси абсцисс.

Творческое задание:
Какие из формул задают линейную функцию? Почему?
y=x3+6
y= 3(x+8)-25 ;
y= 3x-1
Линейная
Линейная
Не линейная
Укажите k и b.
Д.з. №316(б).

Один из жителей деревни отправился на почту получать письмо. За ним побежали его собака с кошкой. Письмо оказалось зашифрованным.Оно содержало описание пути, ведущего к кладу, и место, где он спрятан.
Дом (0;3) Почта (3;0)
Магазин (-2;-1) Колодец (3;4)
Клад находится в точке пересечения прямых, соединяющих дом и почту, магазин и колодец.
Д (0;3) , М(-2;-1) , П(3;0) , К(3;4).
Поможем найти «клад».

Практическая работа.
Д (0;3) , М(-2;-1) , P(3;0) , К(3;4).
Задание:
1)Постройте прямые MK и DP по двум точкам
2)Назовите точку пересечения прямых MK и DP и её координаты.
Координатные прямые- оси координат.
Горизонтальная ось- ось абсцисс.
Вертикальная ось- ось ординат.
Точка пересечения осей координат- начало координат.
Е(1;2)-координаты точки.
1-абсцисса.
2-ордината.
Ответ: (1;2)
E
Д
М
Р
К
Ищем «клад»

Творческое задание:
Точки пересечения графика функции с осями координат.
Д (0;3) - точка пересечения графика функции с осью ординат. (x=0)
P(3;0) – точка пересечения графика функции с осью абсцисс. (y=0)
Запомни:
1) ось абсцисс: y=0
2) ось ординат: x=0
Учебник №322(в)
2) y=1,2x + 6
C осью ординат: x=0
y=1,2 ∙ 0 + 6 , y=6
(0;6)
1) y=1,2x + 6
C осью абсцисс: y=0
0=1,2x+6
-1,2x=6
x = 6 : (-1,2)
x= 60 : (-12)
x= -5 , (-5;0)
Ответ: (-5;0), (0;6)
Д.з. №322(б).

Цифровой диктант.
График функции y = -6x проходит во II и IV координатных четвертях?
График функции y= -8x + 3 проходит через начало координат?
Прямая пропорциональность – частный вид линейной функции?
График функции y= -9 пересекает ось абсцисс?
5)* скорость распространения
звука в воздухе в зависимости от температуры.
(t°)
Задает ли эта формула линейную функцию?
Да - 1 , нет – 0. Назови получившееся число.
Ответ:
10101

Итог урока.
Проверь себя.
1) Что такое линейная функция?
2) Что собой представляет график линейной функции?
3) Дайте определение частного случая линейной функции (прямой пропорциональности)
4)Что собой представляет её график?
Д.з. учебник: стр.65 ,стр.70, №322(б),316(б)