Тема урока: «Правильные многогранники.» ( 2 часа ), 10 классТрофимова Нина Васильевнаучитель математики МОУ средней общеобразова
Содержание
- 2. Содержание Симметрия в пространстве. Правильные многогранники. Элементы симметрии правильных многогранников.
- 3. Цель изучения 1.Познакомить учащихся с симметрией в пространстве. 2.Познакомить учащихся с новым типом выпуклых многогранников –
- 4. Прогнозируемый результат 1.Знать понятия симметричных точек относительно точки, прямой, плоскости; понятия центра, оси и плоскости симметрии
- 5. «Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины
- 6. Ход урока … В планиметрии мы рассматривали фигуры, симметричные относительно точки и относительно прямой. В стереометрии
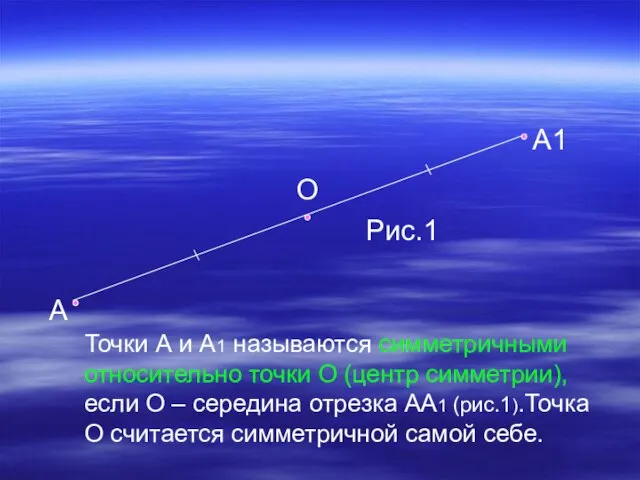
- 7. А1 О А Рис.1 Точки А и А1 называются симметричными относительно точки О (центр симметрии), если
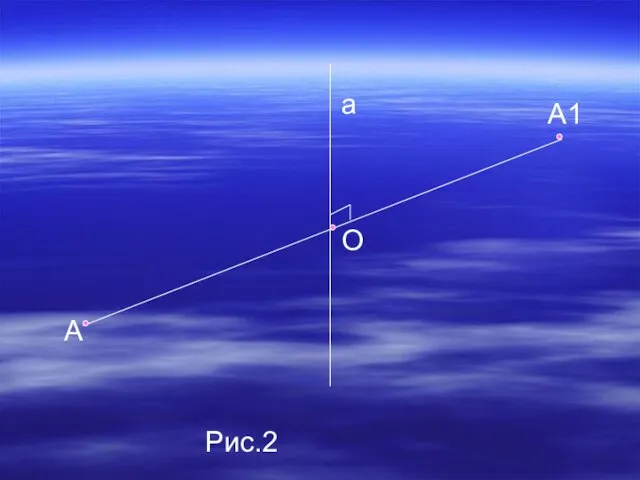
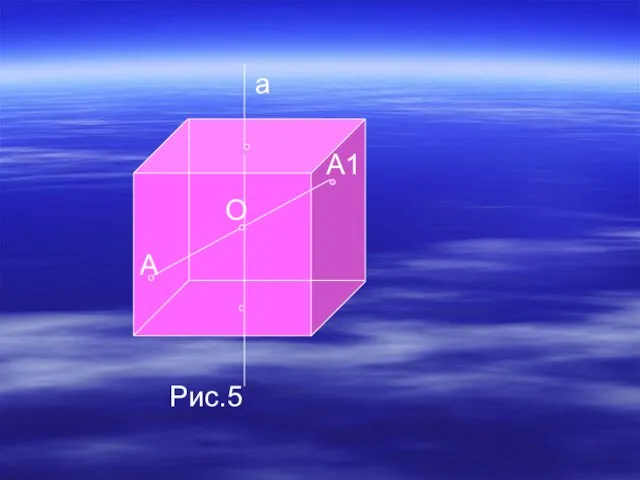
- 8. Точки А и А1 называются симметричными относительно прямой а (ось симметрии), если прямая а проходит через
- 9. А1 а О А Рис.2
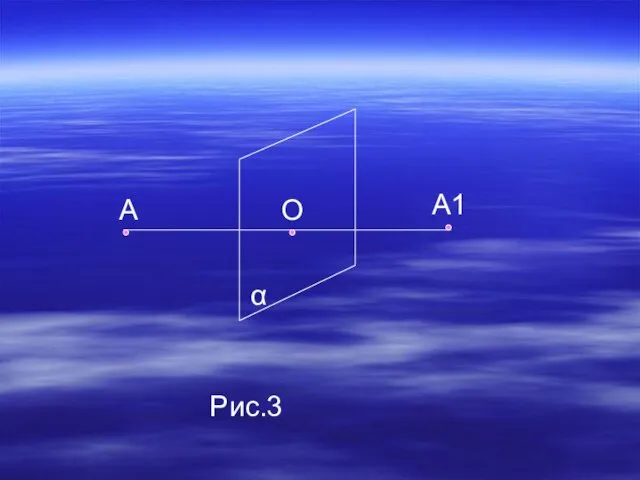
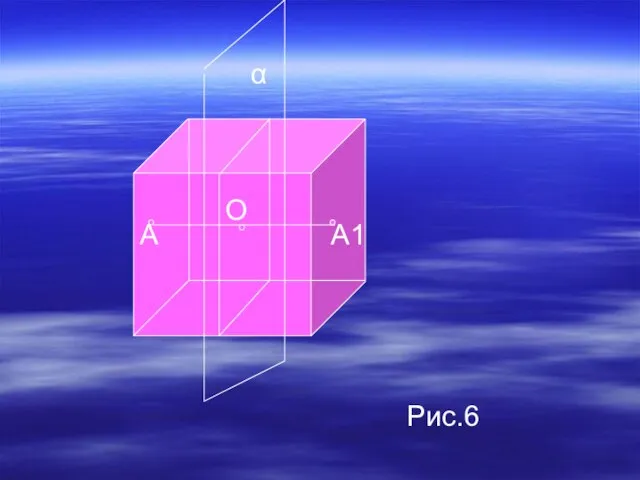
- 10. Точки А и А1 называются симметричными относительно плоскости α (плоскость симметрии), если плоскость α проходит через
- 11. α А О А1 Рис.3
- 12. Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее
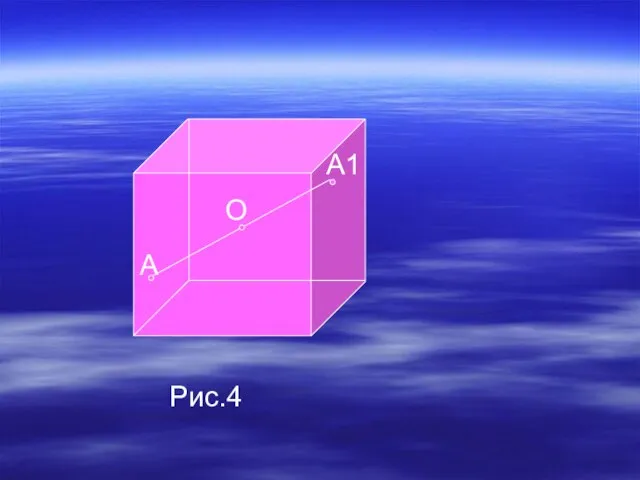
- 13. На рисунках 4,5,6 показаны центр О, ось а и плоскость α симметрии прямоугольного параллелепипеда. Параллелепипед, не
- 14. А О А1 Рис.4
- 15. А О А1 Рис.5 а
- 16. А О А1 α Рис.6
- 17. Фигура может иметь один или несколько центров симметрии (осей, плоскостей симметрии). Например, куб имеет только один
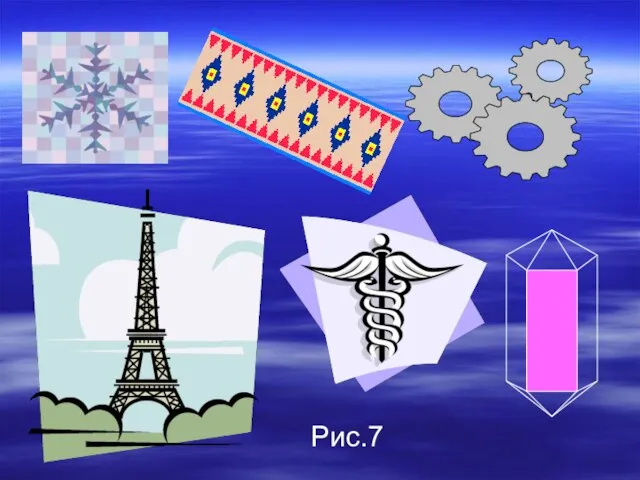
- 18. С симметрией мы часто встречаемся в природе, архитектуре, технике, быту. Так, многие здания симметричны относительно плоскости,
- 19. Рис.7
- 20. … На данный момент Вы уже имеете представление о таких многогранниках как призма и пирамида. Сегодня
- 21. Выпуклый многогранник называется правильным, если все его грани - равные правильные многоугольники и в каждой его
- 22. Докажем, что не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n –
- 23. Если n = 4, то α = 90°, грани многогранника – квадраты. 90°·3 = 270° 360°.
- 24. Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма
- 25. Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма
- 26. Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма
- 27. Куб (гексаэдр) составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских
- 28. Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно,
- 29. Названия этих многогранников пришли из Древней Греции, и в них указывается число граней: «эдра» - грань
- 30. «Правильные многогранники в философской картине мира Платона» Правильные многогранники иногда называют платоновыми телами, поскольку они занимают
- 31. А теперь от Древней Греции перейдём к Европе Х\/I – Х\/ІІ вв., когда жил и творил
- 32. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса
- 33. Модель Солнечной системы И. Кеплера
- 34. Идеи Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира и в наше время
- 35. Рис.8
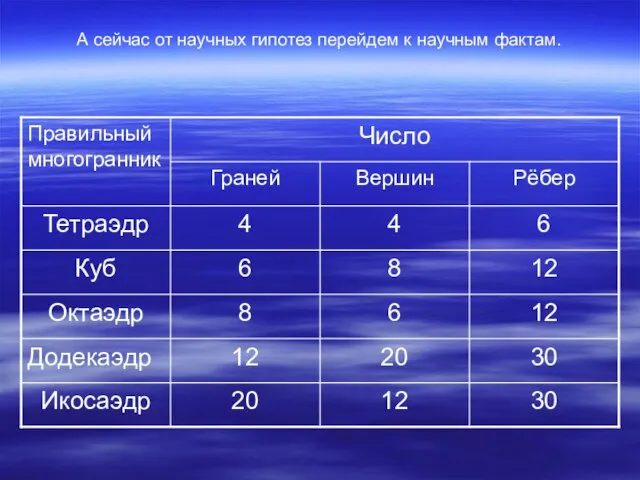
- 36. А сейчас от научных гипотез перейдем к научным фактам.
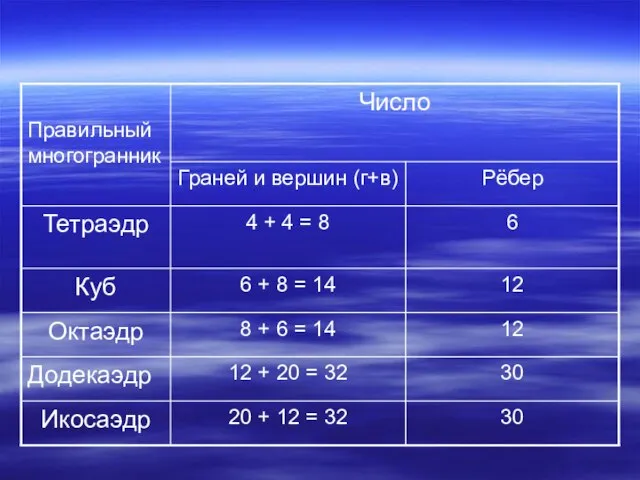
- 38. Г + В = Р + 2 Эта формула была подмечена уже Декартом в 1640 г.,
- 39. «Тайная вечеря»
- 43. Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр. Чем
- 44. Феодария
- 45. Радиолария
- 46. Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых
- 47. Элементы симметрии правильных многогранников Правильный тетраэдр не имеет центра симметрии, имеет три оси симметрии и шесть
- 48. Тест 1.Какое из перечисленных геометрических тел не является правильным многогранником? а) правильный тетраэдр; б) правильный гексаэдр;
- 49. б) сумма плоских углов при вершине правильного додекаэдра равна 324°; в) куб имеет два центра симметрии
- 51. Скачать презентацию







































 Народные сказки Ю.Мориц "Сказка по лесу идёт..." 2 класс
Народные сказки Ю.Мориц "Сказка по лесу идёт..." 2 класс Diesel Engines
Diesel Engines  Органическая химия в быту
Органическая химия в быту Творчество А.Блока
Творчество А.Блока Состав лекарственных растений Терапевтическая ценность Биологически активные вещества Заготовка лекарственного растительного
Состав лекарственных растений Терапевтическая ценность Биологически активные вещества Заготовка лекарственного растительного  Презентация на тему Путь к свободе через красоту
Презентация на тему Путь к свободе через красоту Военная присяга
Военная присяга ТЭК-Торг. Некоторые изменения вносимые Федеральным законом №277-ФЗ от 02.07.2021
ТЭК-Торг. Некоторые изменения вносимые Федеральным законом №277-ФЗ от 02.07.2021 НАШИ ВОЗМОЖНОСТИ
НАШИ ВОЗМОЖНОСТИ Пионерская дружина имени Ю.А. Гагарина ООШ с. Малый Седякфилиал МОБУ СОШ №1 с. Бижбуляк
Пионерская дружина имени Ю.А. Гагарина ООШ с. Малый Седякфилиал МОБУ СОШ №1 с. Бижбуляк Файлы
Файлы Стажировка студентов факультета психологии, социальной медицины и реабилитационных технологий в университете им. Масарик Чехия
Стажировка студентов факультета психологии, социальной медицины и реабилитационных технологий в университете им. Масарик Чехия Точка Фест
Точка Фест Опыт создания единой информационной среды школы
Опыт создания единой информационной среды школы Пуантилизм. Главная особенность
Пуантилизм. Главная особенность Презентация на тему Закрепление табличного умножения и деления
Презентация на тему Закрепление табличного умножения и деления 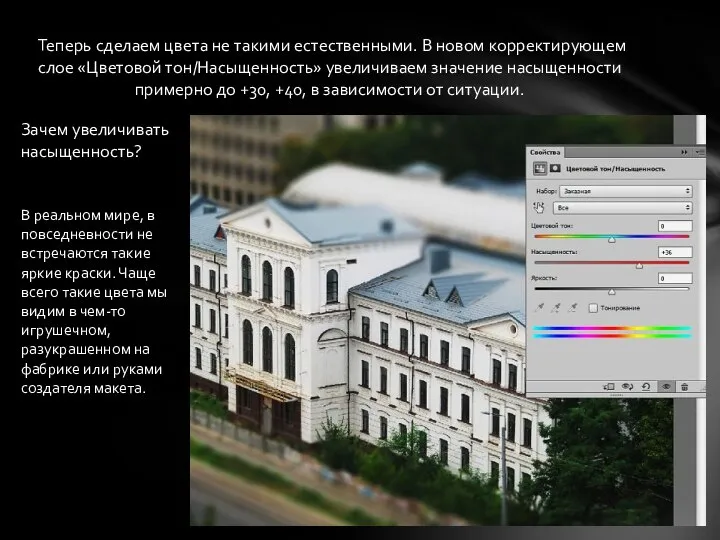 Выравнивание экспозиции
Выравнивание экспозиции Образовательно-воспитательная программа «Я- гражданин России» - от апробации к основам воспитательной системы класса
Образовательно-воспитательная программа «Я- гражданин России» - от апробации к основам воспитательной системы класса Животноводство
Животноводство Из опыта реализации гендерного подхода к образованию(на примере класса девочек)
Из опыта реализации гендерного подхода к образованию(на примере класса девочек) Water Drop
Water Drop Презентация на тему Осень и зима в жизни растений
Презентация на тему Осень и зима в жизни растений Галогены и их соединения
Галогены и их соединения Lotus Domino/Notes – оптимальная платформа для построения систем электронного документооборота
Lotus Domino/Notes – оптимальная платформа для построения систем электронного документооборота Межмуниципальное сотрудничество
Межмуниципальное сотрудничество Презентация на тему Природные источники углеводородов и их переработка
Презентация на тему Природные источники углеводородов и их переработка Жанр портрета в культуре разных времён
Жанр портрета в культуре разных времён Сервис
Сервис