Тема урока: «Решение задач»

Цели урока
Повторить понятия медианы, биссектрисы, высоты треугольника;
Повторить свойства равнобедренного треугольника; показать применение данных понятий при решении геометрических задач.

Решение задач по медианам, биссектрисам, высотам треугольника.
Равнобедренный треугольник.
21.11.07

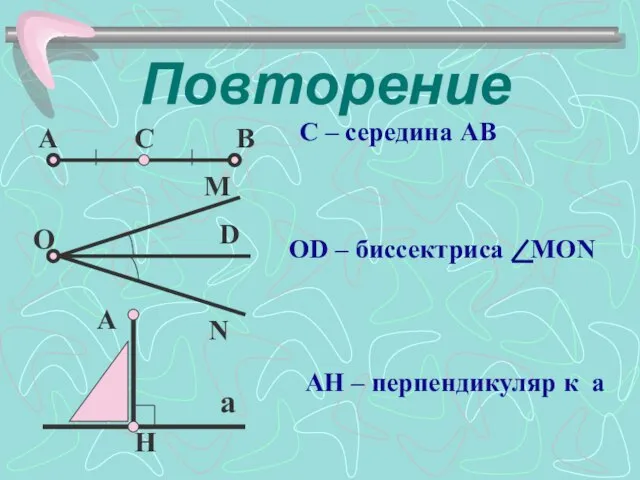
Повторение
С – середина АВ
AH – перпендикуляр к а

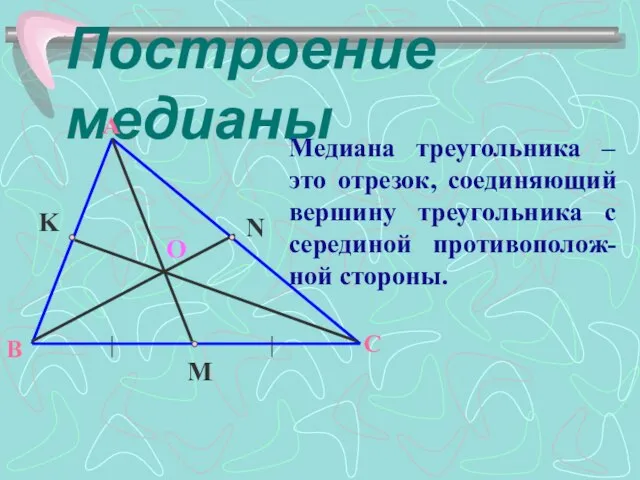
Построение медианы
O
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противополож-ной стороны.

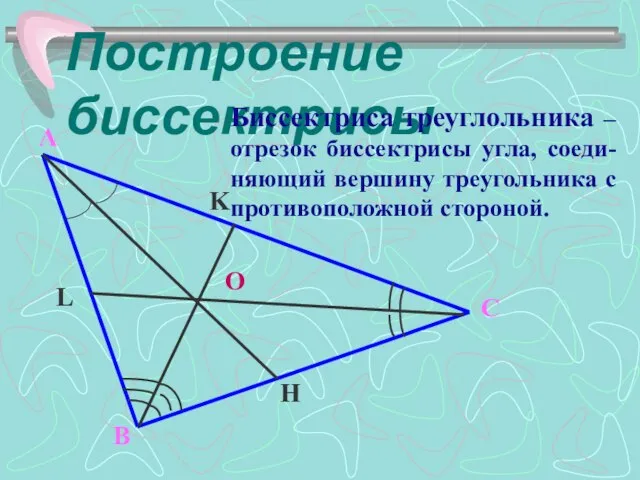
Построение биссектрисы
H
K
L
O
Биссектриса треуглольника – отрезок биссектрисы угла, соеди-няющий вершину треугольника с противоположной стороной.

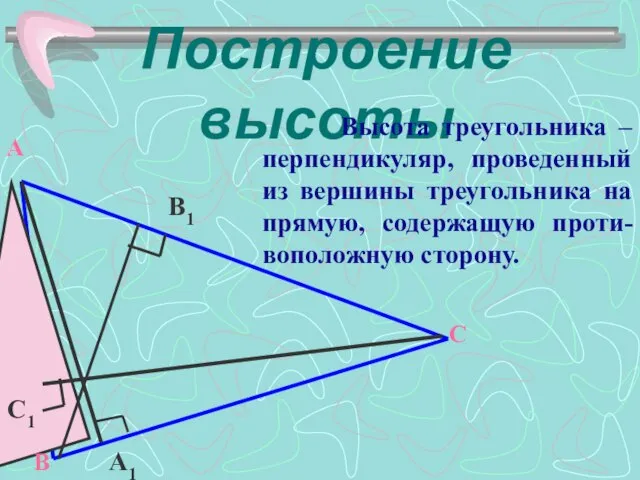
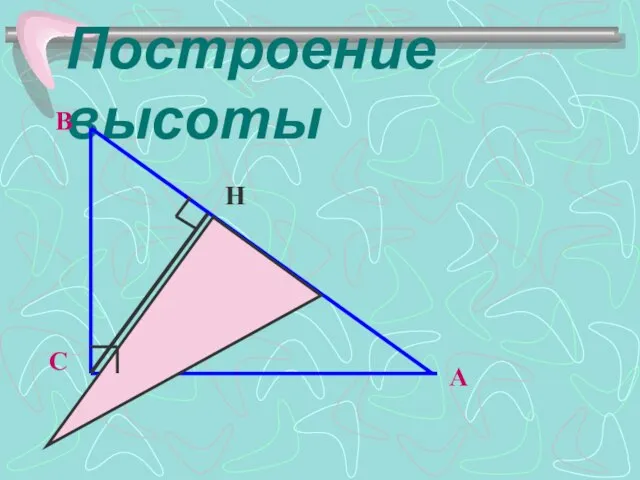
Построение высоты
Высота треугольника – перпендикуляр, проведенный из вершины треугольника на прямую, содержащую проти-воположную сторону.
A1
C1
B1

Построение высоты
H

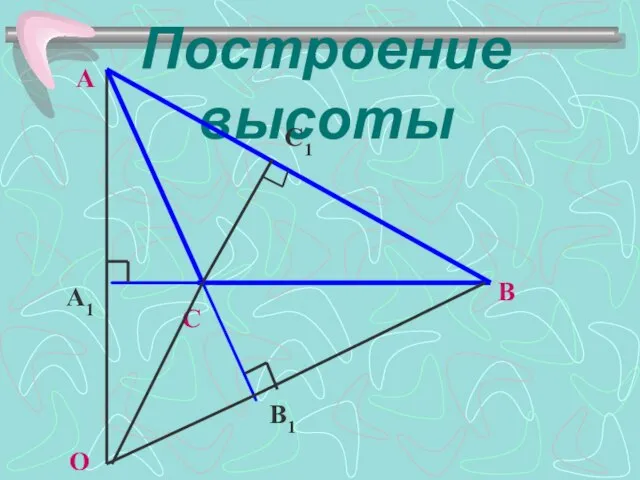
Построение высоты
C1
B1
A1
O

Основные свойства медиан,
биссектрис и высот.
Медианы треугольника пересекаются
в одной точке, внутри треугольника.
2. Биссектрисы треугольника пересекаю-
тся в одной точке, внутри треугольника.
3. Высоты треугольника пересекаются
в одной точке внутри треугольника
или на сторонах прямого угла, или
на продолжении сторон тупого угла.

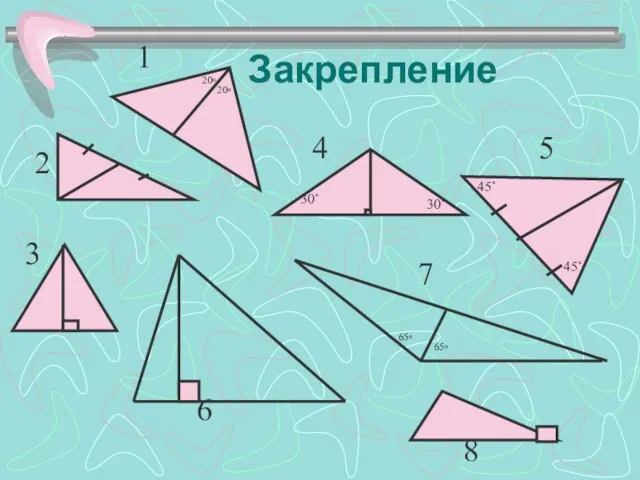
Закрепление
65◦
65◦
20◦
20◦
1
2
3
4
5
6
7
8
30˚
30˚
45˚
45˚

Медиана: 2, 5.
Высота: 3, 6, 8, 4.
Биссектриса: 1, 7.
Равнобедренные треугольники: 4,5.

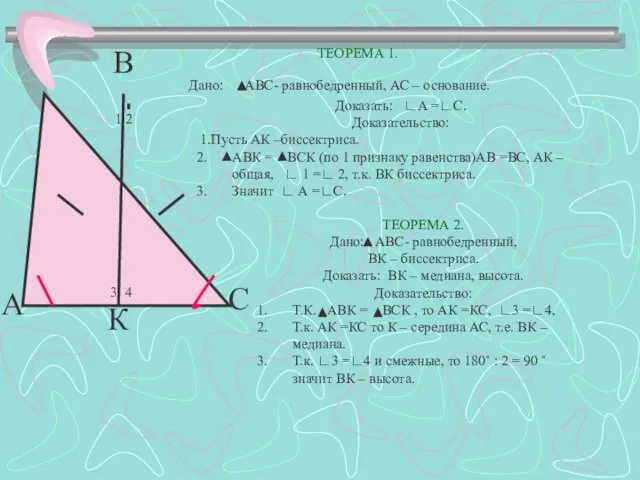
А
В
С
К
Дано: АВС- равнобедренный, АС – основание.
Доказать: ∟А =∟С.
Доказательство:
1.Пусть АК –биссектриса.
АВК = ВСК (по 1 признаку равенства)АВ =ВС, АК – общая, ∟ 1 =∟ 2, т.к. ВК биссектриса.
Значит ∟ А =∟С.
1
2
ТЕОРЕМА 2.
Дано: АВС- равнобедренный,
ВК – биссектриса.
Доказать: ВК – медиана, высота.
Доказательство:
Т.К. АВК = ВСК , то АК =КС, ∟3 =∟4,
Т.к. АК =КС то К – середина АС, т.е. ВК –медиана.
Т.к. ∟3 =∟4 и смежные, то 180˚ : 2 = 90 ˚ значит ВК – высота.
3
4
ТЕОРЕМА 1.

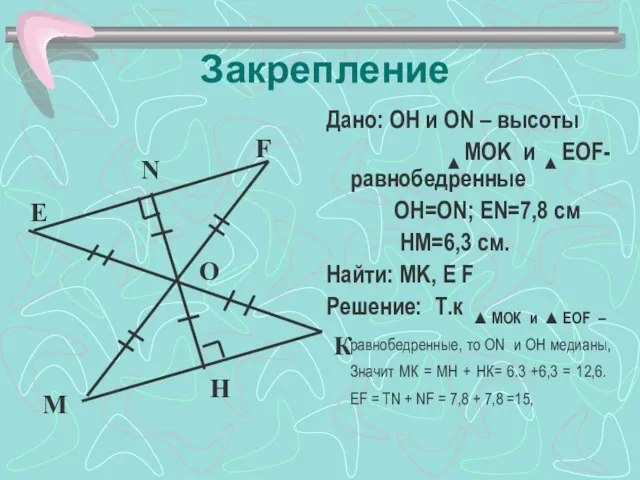
Закрепление
Дано: ОH и ON – высоты
▲MOK и ▲EOF- равнобедренные
ОH=ОN; EN=7,8 см
HM=6,3 см.
Найти: MK, Е F
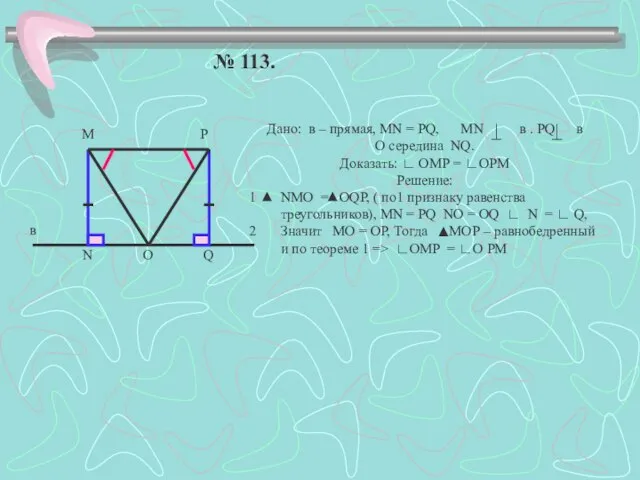
Решение: Т.к ▲МОК и ▲ЕОF –равнобедренные, то ОN и OH медианы, Значит МК = МН + НК= 6.3 +6,3 = 12,6. ЕF = TN + NF = 7,8 + 7,8 =15,

№ 113.
в
М
Р
О
N
Q
Дано: в – прямая, МN = PQ, MN в . PQ в
О середина NQ.
Доказать: ∟ ОМР = ∟ОРМ
Решение:
NMO = OQP, ( по1 признаку равенства треугольников), MN = PQ NO = OQ ∟ N = ∟ Q,
Значит МО = ОР, Тогда МОР – равнобедренный и по теореме 1 => ∟ОМР = ∟О РМ

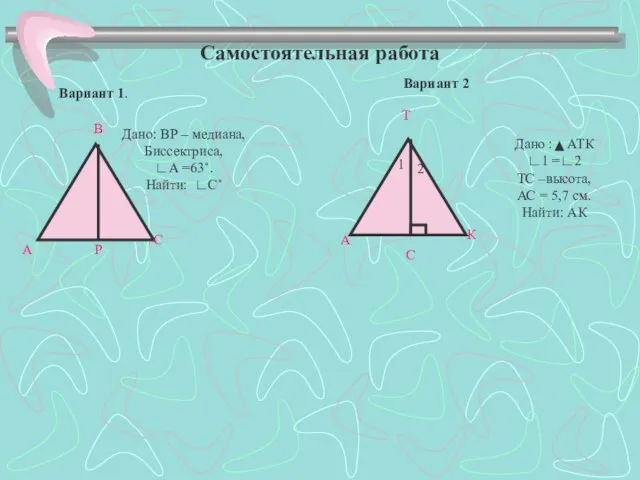
Самостоятельная работа
Вариант 1.
А
В
С
Р
Дано: ВР – медиана,
Биссектриса,
∟А =63˚.
Найти: ∟С˚
А
С
К
Т
1
2
Вариант 2
Дано : АТК
∟1 =∟2
ТС –высота,
АС = 5,7 см.
Найти: АК