Содержание
- 2. Теория Автоматического Управления Цель курса состоит в изучении принципов автоматического управления, типов систем автоматического управления, используемых
- 3. 1.1. Общие понятия 1.2. Фундаментальные принципы управления 2.1. Основные виды САУ 2.2. Статические характеристики 2.3. Статическое
- 4. 1.1 Общие понятия Теория автоматического управления (ТАУ) появилась во второй половине 19 века сначала как теория
- 5. 1.2 Фундаментальные принципы управления 1.2.1. Принцип разомкнутого управления 1.2.2. Принцип компенсации 1.2.3. Принцип обратной связи
- 6. 1.2.1. Принцип разомкнутого управления Рассмотрим САУ хлебопекарной печи (рис.1). Ее принципиальная схема показывает принцип действия данной
- 7. Часть ОУ, которая преобразует управляемую величину в пропорциональную ей величину, удобную для использования в САУ, называют
- 8. Задающим устройством (ЗУ) называется устройство, задающее программу изменения управляющего воздействия, то есть формирующее задающий сигнал uо(t).
- 9. 1.2.2. Принцип компенсации Если возмущающий фактор искажает выходную величину до недопустимых пределов, то применяют принцип компенсации
- 10. 1.2.2. Принцип компенсации Примеры систем компенсации: биметаллический маятник в часах, компенсационная обмотка машины постоянного тока и
- 11. 1.2.3. Принцип обратной связи Наибольшее распространение в технике получил принцип обратной связи (рис.7). Здесь управляющее воздействие
- 12. 1.2.3. Принцип обратной связи В частном случае (рис.8) ЗУ формирует требуемое значение выходной величины yо(t), которое
- 13. 1.2.3. Принцип обратной связи Такое управление в функции отклонения называется регулированием, а подобную САУ называют системой
- 14. Недостатком принципа обратной связи является инерционность системы. Поэтому часто применяют комбинацию данного принципа с принципом компенсации,
- 15. 2.1. Основные виды САУ В зависимости от принципа и закона функционирования ЗУ, задающего программу изменения выходной
- 16. 2.1. Основные виды САУ Следящие системы отличаются от программных лишь тем, что программа y = f(t)
- 17. 2.1. Основные виды САУ Так в экстремальных системах (рис.12) требуется, чтобы выходная величина всегда принимала экстремальное
- 18. Оптимальные системы являются более сложным вариантом экстремальных систем. Здесь происходит, как правило, сложная обработка информации о
- 19. 2.2. Статические характеристики Режим работы САУ, в котором управляемая величина и все промежуточные величины не изменяются
- 20. 2.2. Статические характеристики Так примером одного из функциональных звеньев системы регулирования воды в баке является обычный
- 21. 2.2. Статические характеристики Статическая характеристика данного звена имеет вид отрезка прямой линии с наклоном a =
- 22. 2.2. Статические характеристики Например, статическая характеристика насыщенного генератора постоянного тока представлена на рис.16. Обычно нелинейная характеристика
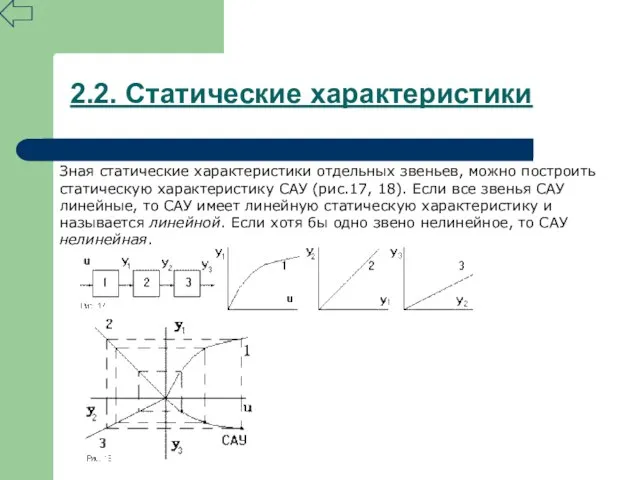
- 23. 2.2. Статические характеристики Зная статические характеристики отдельных звеньев, можно построить статическую характеристику САУ (рис.17, 18). Если
- 24. 2.2. Статические характеристики Звенья, для которых можно задать статическую характеристику в виде жесткой функциональной зависимости выходной
- 25. 2.3. Статическое и астатическое регулирование Если на управляемый процесс действует возмущение f, то важное значение имеет
- 26. Рассмотрим систему регулирования уровня воды в баке (рис.20). Возмущающим фактора является поток Q воды из бака.
- 27. 2.3. Статическое и астатическое регулирование Статические регуляторы работают при обязательном отклонении e регулируемой величины от требуемого
- 28. 2.3. Статическое и астатическое регулирование Статизм d, САР, характеризует насколько сильно значение регулируемой величины отклоняется от
- 29. Для того, чтобы получить астатическое регулирование, необходимо в регулятор включить астатическое звено, например ИД, между ЧЭ
- 30. 3.1. Динамический режим САУ. Управление динамики Установившийся режим не является характерным для САУ. Обычно на управляемый
- 31. 3.1. Динамический режим САУ. Управление динамики При резких возмущениях возможен колебательный затухающий процесс (рис.25а). Существует и
- 32. 3.1. Динамический режим САУ. Управление динамики Таким образом, основным режимом работы САУ считается динамический режим, характеризующийся
- 33. 3.2. Линеаризация уравнения динамики В общем случае уравнение динамики оказывается нелинейным, так как реальные звенья САУ
- 34. 3.2. Линеаризация уравнения динамики В нормально функционирующей САУ значение регулируемой и всех промежуточных величин незначительно отличается
- 35. 3.2. Линеаризация уравнения динамики Математическое обоснование линеаризации состоит в том, что если известно значение f(a) какой
- 36. 3.2. Линеаризация уравнения динамики В номинальном режиме, когда все отклонения и их производные по времени равны
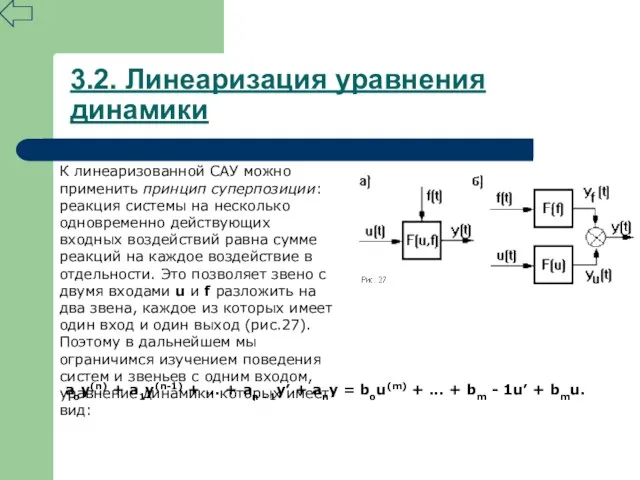
- 37. 3.2. Линеаризация уравнения динамики К линеаризованной САУ можно применить принцип суперпозиции: реакция системы на несколько одновременно
- 38. 3.2. Линеаризация уравнения динамики Это уравнение описывает САУ в динамическом режиме лишь приближенно с той точностью,
- 39. 3.3. Передаточная функция В ТАУ часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие
- 40. 3.3. Передаточная функция Поэтому уравнение динамики можно записать также в виде: Дифференциальный оператор W(p) называют передаточной
- 41. 3.3. Передаточная функция Звено САУ с известной передаточной функцией называется динамическим звеном. Оно изображается прямоугольником, внутри
- 42. 3.4. Элементарные динамические звенья Динамика большинства функциональных элементов САУ независимо от исполнения может быть описана одинаковыми
- 43. 3.4. Элементарные динамические звенья То есть Корни любого полинома могут быть либо вещественными pi = ai
- 44. 3.4. Элементарные динамические звенья Поэтому любую сложную передаточную функцию линеаризованной САУ можно представить как произведение передаточных
- 45. 4.1. Эквивалентные преобразования структурных схем Структурная схема САУ в простейшем случае строится из элементарных динамических звеньев.
- 46. 4.1. Эквивалентные преобразования структурных схем 2. Параллельно - согласное соединение (рис.29) - на вход каждого звена
- 47. 4.1. Эквивалентные преобразования структурных схем 3. Прараллельно - встречное соединение (рис. 30а) - звено охвачено положительной
- 48. 4.1. Эквивалентные преобразования структурных схем Замкнутую систему называют одноконтурной, если при ее размыкании в какой либо
- 49. 4.1. Эквивалентные преобразования структурных схем Для положительной ОС в знаменателе знак минус. Если сменить точку снятия
- 50. 4.1. Эквивалентные преобразования структурных схем Если многоконтурная система имеет перекрещивающиеся связи (рис.33), то для вычисления эквивалентной
- 51. 4.1. Эквивалентные преобразования структурных схем Так с выхода системы на рис.34а снимается сигнал Такой же сигнал
- 52. 4.1. Эквивалентные преобразования структурных схем 5. При переносе узла через звено по ходу сигнала добавляется звено
- 53. 4.1. Эквивалентные преобразования структурных схем 6. Возможны взаимные перестановки узлов и сумматоров: узлы можно менять местами
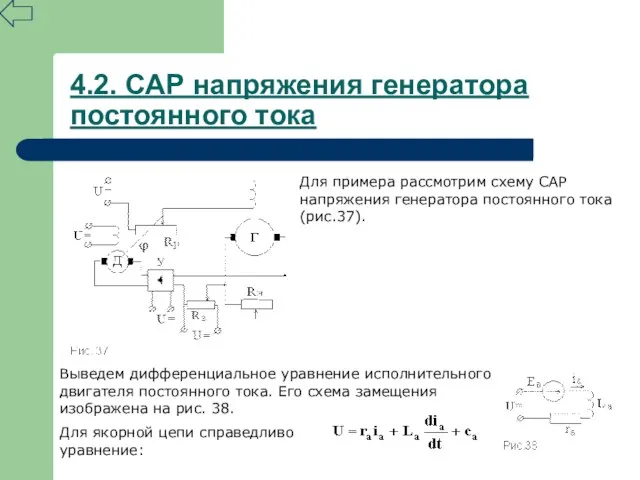
- 54. 4.2. САР напряжения генератора постоянного тока Для примера рассмотрим схему САР напряжения генератора постоянного тока (рис.37).
- 55. 4.2. САР напряжения генератора постоянного тока Если принять, что , где – угол поворота вала двигателя,
- 56. 4.2. САР напряжения генератора постоянного тока Следовательно = > = > = > = > =
- 57. 4.2. САР напряжения генератора постоянного тока – передаточные функции по напряжению и моменту сторонних сил. Структурная
- 58. 5.1. Понятие временных характеристик Для оценки динамических свойств системы и отдельных звеньев принято исследовать их реакцию
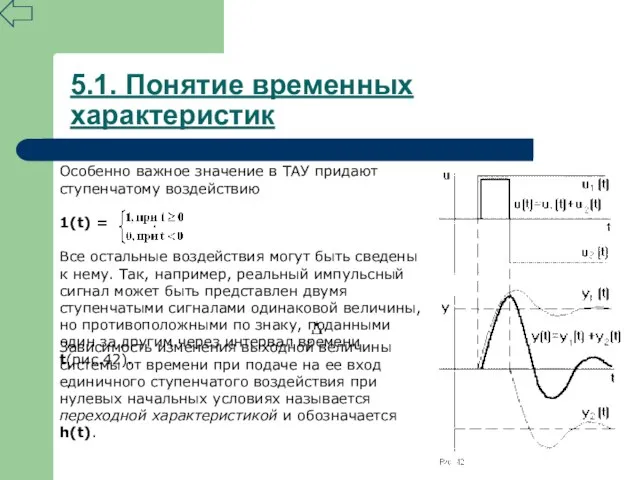
- 59. Особенно важное значение в ТАУ придают ступенчатому воздействию 1(t) = . Все остальные воздействия могут быть
- 60. 5.1. Понятие временных характеристик Не менее важное значение в ТАУ уделяется импульсной переходной характеристике, которая описывает
- 61. 5.2.1. Безынерционное (пропорциональное, усилительное) звено 5.2.2. Интегрирующее (астатическое) звено 5.2.3. Инерционное звено первого порядка (апериодическое) 5.2.4.
- 62. 5.2.1. Безынерционное (пропорциональное, усиленное)звено Это звено, для которого в любой момент времени выходная величина пропорциональна входной.
- 63. 5.2.2. Интегрирующее (астатическое) звено Его уравнение: или Передаточная функция: Переходная характеристика: (рис.44) При k = 1
- 64. 5.2.3. Инерционное звено первого порядка (апериодическое) Уравнение динамики: , или Передаточная функция: Переходная характеристика может быть
- 65. 5.2.3. Инерционное звено первого порядка (апериодическое) Переходная характеристика имеет вид экспоненты (рис.45), по которой можно определить
- 66. 5.2.4. Инерционные звенья второго порядка Его уравнение: Передаточная функция: Решение уравнения зависит от соотношения постоянных времени
- 67. 5.2.4. Инерционные звенья второго порядка Такое звено можно разложить на два апериодических звена первого порядка, поэтому
- 68. 5.2.5. Дифференцирующее звено Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики идеального звена: , или y
- 69. При малых Т звено можно рассматривать как идеальное дифференцирующее. Переходную характеристики можно вывести с помощью формулы
- 70. 6.1. Понятие частотных характеристик Если подать на вход системы с передаточной функцией W(p) гармонический сигнал то
- 71. 6.1. Понятие частотных характеристик Учтем, что а значит pnu = pnUmejwt = Um (jw)nejwt = (jw)nu.
- 72. 6.1. Понятие частотных характеристик W(j ) есть комплексная функция, поэтому: где P( ) - вещественная ЧХ
- 73. 6.1. Понятие частотных характеристик В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) (рис.49): логарифмическая амплитудная ЧХ
- 74. 6.1. Понятие частотных характеристик Так как мощность гармонического сигнала Р пропорциональна квадрату его амплитуды А, то
- 75. 6.2.1. Безынерционное звено 6.2.2. Интегрирующее звено 6.2.3. Апериодическое звено 6.2.4. Инерционные звенья второго порядка 6.2.5. Правила
- 76. 6.2.1. Безынерционное звено Передаточная функция: W(p) = k. АФЧХ: W(j ) = k. ВЧХ: P( )
- 77. 6.2.2. Интегрирующее звено Передаточная функция: W(p) = k/p. Рассмотрим частный случай, когда k = 1, то
- 78. 6.2.3. Апериодическое звено При k = 1 получаем следующие выражения ЧХ: Здесь A1 и A2 -
- 79. 6.2.3. Апериодическое звено ЧХ показаны на рис.52. АФЧХ есть полуокружность радиусом 1/2 с центром в точке
- 80. 6.2.4. Инерционные звенья второго порядка При k = 1 передаточная функция звена: В виду сложности вывода
- 81. 6.2.5. Правила построения ЧХ элементарных звеньев При построении ЧХ некоторых звеньев можно использовать “правило зеркала”: при
- 83. Скачать презентацию












































































 Как построить гараж?
Как построить гараж? Оптическое просветление биологических тканей – перспективы применения в медицинской диагностике и фототерапии
Оптическое просветление биологических тканей – перспективы применения в медицинской диагностике и фототерапии Дорожное движение, безопасность участников дорожного движения (5 класс)
Дорожное движение, безопасность участников дорожного движения (5 класс) Профессия – ученик
Профессия – ученик Один путь к Богу
Один путь к Богу О денежно-кредитной политике инновационного экономического развития
О денежно-кредитной политике инновационного экономического развития Презентация о стрекозах...
Презентация о стрекозах... Презентация Слива
Презентация Слива Изменения в законе РФ О занятости населения в Российской Федерации. Информация для работодателей
Изменения в законе РФ О занятости населения в Российской Федерации. Информация для работодателей Ян Вермеер Делфтеский (картины)
Ян Вермеер Делфтеский (картины) Законы Кеплера
Законы Кеплера Презентация на тему Как написать сочинение
Презентация на тему Как написать сочинение Презентация на тему Составное глагольное сказуемое
Презентация на тему Составное глагольное сказуемое  Презентация на тему Происхождение человека. Человеческие расы
Презентация на тему Происхождение человека. Человеческие расы  день отца
день отца Тема 2 Система и источники МЧП
Тема 2 Система и источники МЧП Национальные традиции, обычаи, культура народов нашего края
Национальные традиции, обычаи, культура народов нашего края Решение задач повышенного уровня
Решение задач повышенного уровня Як заповнити оціночну форму
Як заповнити оціночну форму История кино. Кинематограф
История кино. Кинематограф Презентация Сущность и функции методологического подхода
Презентация Сущность и функции методологического подхода Stili_rechi_ISP9-21_Sidorov
Stili_rechi_ISP9-21_Sidorov Настольные игры от разработчиков
Настольные игры от разработчиков Куклы - обереги 4 класс
Куклы - обереги 4 класс Прогностика, пророчества и осуществление единственного будущего
Прогностика, пророчества и осуществление единственного будущего О Программе «Национальная банковская система России 2010, 2020»
О Программе «Национальная банковская система России 2010, 2020» Размножение организмов 6 класс
Размножение организмов 6 класс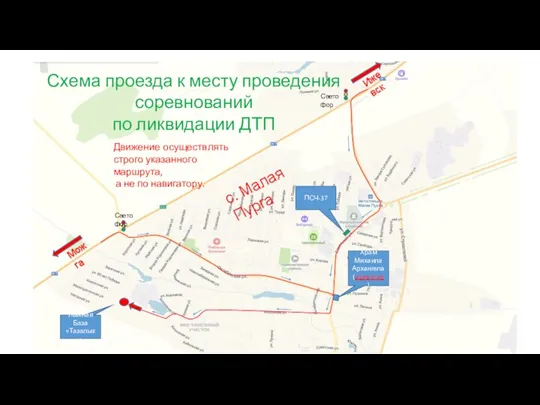 Схема проезда к месту проведения соревнований по ликвидации ДТП, лыжная база Тазалык
Схема проезда к месту проведения соревнований по ликвидации ДТП, лыжная база Тазалык