Теория движения военных колесных машин. Слайды к лекциям по курсу. Лекция 9

Распределение крутящих моментов и
окружных сил по колесам
В сложной динамической системе колесной машины крутящие моменты на всех валах и колесах беспрерывно изменяются. Это объясняется не только многообразием процессов и связей, имеющихся в самой КМ, но и влиянием переменных внешних условий, на которые автоматически или по воле водителя она реагирует.
Однако при относительно постоянных условиях, например при движении КМ с постоянной скоростью по ровной ОП, изменение крутящих моментов невелико (средние квадратичные отклонения моментов Mк на колесах не превышает 15…20% от их средней величины).
В механической трансмиссии поток мощности передается к колесам через узлы разветвления, в которых могут изменяться значения моментов и угловых скоростей на выходных валах по сравнению с параметрами входного вала.

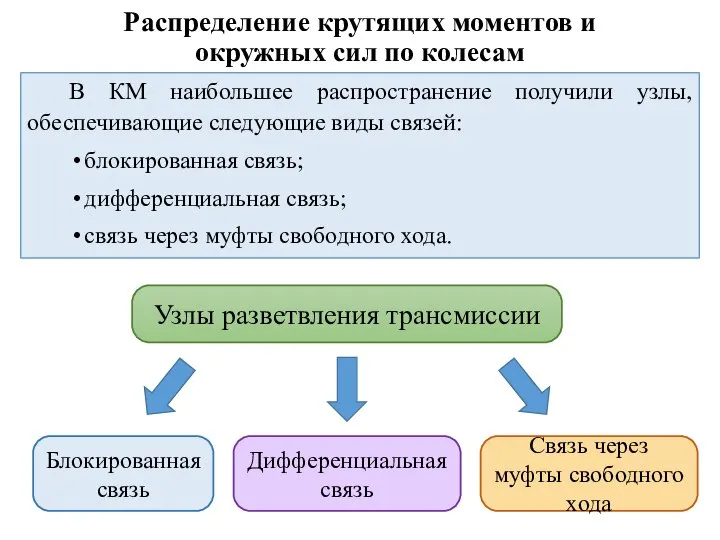
В КМ наибольшее распространение получили узлы, обеспечивающие следующие виды связей:
блокированная связь;
дифференциальная связь;
связь через муфты свободного хода.
Узлы разветвления трансмиссии
Блокированная связь
Дифференциальная связь
Связь через муфты свободного хода
Распределение крутящих моментов и
окружных сил по колесам

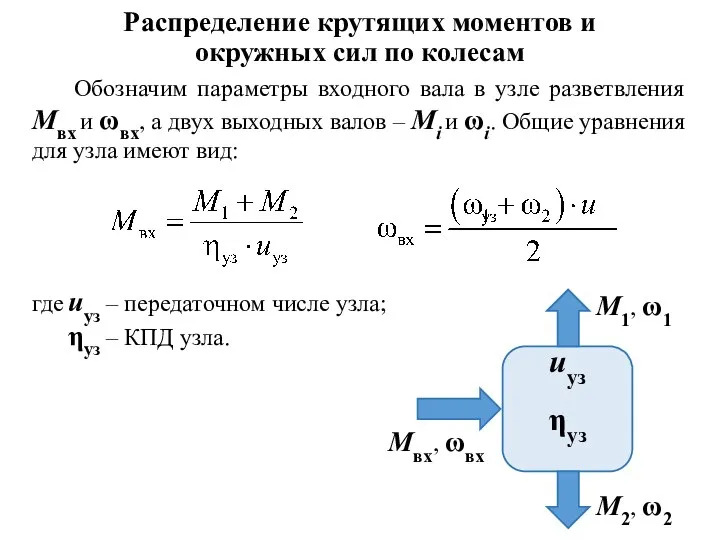
Обозначим параметры входного вала в узле разветвления Мвх и ωвх, а двух выходных валов – Мi и ωi. Общие уравнения для узла имеют вид:
где uуз – передаточном числе узла;
ηуз – КПД узла.
uуз
ηуз
Мвх, ωвх
М1, ω1
М2, ω2
Распределение крутящих моментов и
окружных сил по колесам

При uуз = 1 и u12 = 1 все угловые скорости равны: ωвх = ω1 = ω2
Блокированная связь
В случае блокированной связи при отсутствии механизма, изменяющего отношение угловых скоростей выходных валов (u12 = 1), должно выполняться условие ω1 = ω2.
Распределение крутящих моментов и
окружных сил по колесам

Распределение крутящих моментов и
окружных сил по колесам
Дифференциальная связь с коэффициентом блокировки kбл
После достижения отношения моментов на выходных валах, равного коэффициенту блокировки дифференциала:
должны выполняться условия
Если M2/M1 < kбл, то узел ведет себя как блокированная связь, дифференциальные свойства проявляются только при M2/M1 > kбл.

Распределение крутящих моментов и
окружных сил по колесам
При одинаковых знаках выходных моментов (M2/M1 > 0) узел ведет себя как блокированная связь.
Связь через муфты свободного хода
В случае если один из моментов становится отрицательным, то весь момент Mвх поступает на другой вал, а вал с отрицательным значением момента отключается.

На автомобилях с одной ведущей осью, как правило, устанавливают симметричный дифференциал с передаточным числом между валами u12 = 1, а также коэффициентом блокировки, близким к 1.
В таком случае, моменты на колесах правого и левого бортов практически равны (Mк1 ≈ Mк2), и при прямолинейном движении можно говорить о равенстве окружных сил на колесах.
Распределение крутящих моментов и
окружных сил по колесам
В ведомом режиме радиусы качения колес бортов оси и их окружные силы Рк = Мк/rк0 обычно различаются не более чем на 2...3 %.

Предполагая, что при прямолинейном движении условия взаимодействия колес бортов оси с опорной поверхностью и их характеристики одинаковы Мк1 = Мк2, рассмотрим лишь влияние межосевого привода на распределение моментов и сил.
Проведем оценку распределения мощности на примере прямолинейного движения и деления момента между мостами (не рассматривая бортовые связи).
Распределение крутящих моментов и
окружных сил по колесам
В многоприводных КМ возможно много вариантов схем трансмиссий, которые приводят к различному распределению моментов и сил.

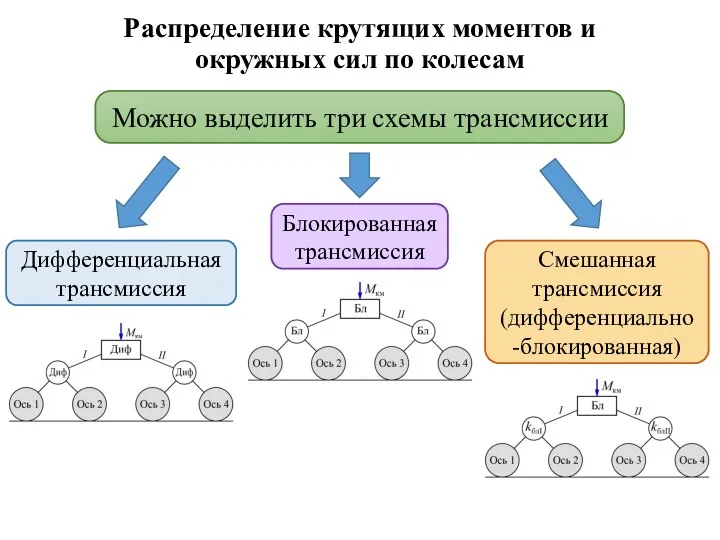
Распределение крутящих моментов и
окружных сил по колесам
Можно выделить три схемы трансмиссии
Дифференциальная трансмиссия
Блокированная трансмиссия
Смешанная трансмиссия (дифференциально-блокированная)

Например, на трехосной КМ момент Мвх, поступающий на раздаточную коробку, распределяется в соотношении:
1/3 от Мвх на первую ось;
2/3 от Мвх на заднюю тележку с двумя осями,
т. е. передаточное число между ними u1-23 = 2.
Тогда крутящие моменты на всех колесах одинаковы:
Mкi =Мк = const.
В этом случае КМ имеет полностью дифференциальную схему трансмиссии с kбл = 1.
В соответствии с характеристиками дифференциалов возможны следующие варианты:
1. Во всех узлах разветвлений установлены симметричные дифференциалы u12 = 1 с kбл = 1 или в некоторых узлах установлены несимметричные дифференциалы u12 ≠ 1 с kбл = 1.
Дифференциальная трансмиссия

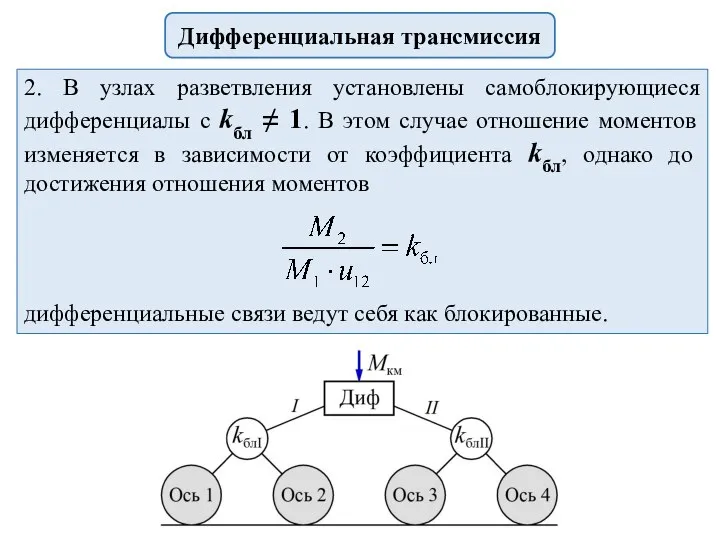
Дифференциальная трансмиссия
2. В узлах разветвления установлены самоблокирующиеся дифференциалы с kбл ≠ 1. В этом случае отношение моментов изменяется в зависимости от коэффициента kбл, однако до достижения отношения моментов
дифференциальные связи ведут себя как блокированные.

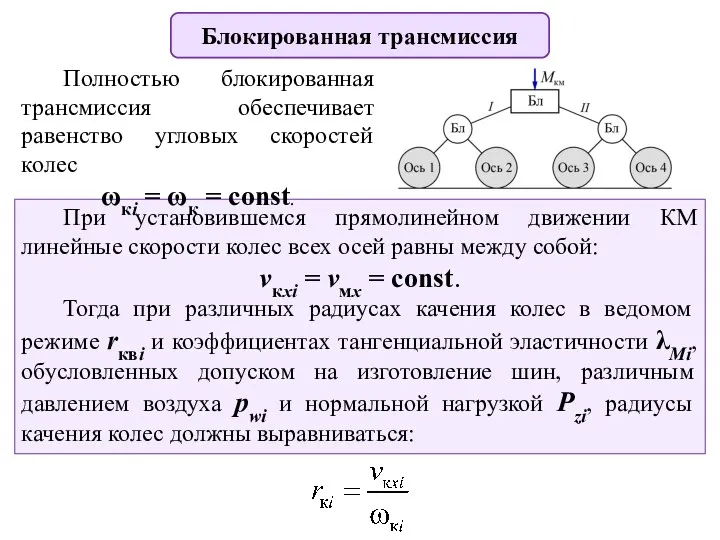
Блокированная трансмиссия
При установившемся прямолинейном движении КМ линейные скорости колес всех осей равны между собой:
vкxi = vмx = const.
Тогда при различных радиусах качения колес в ведомом режиме rквi и коэффициентах тангенциальной эластичности λMi, обусловленных допуском на изготовление шин, различным давлением воздуха pwi и нормальной нагрузкой Pzi, радиусы качения колес должны выравниваться:
Полностью блокированная трансмиссия обеспечивает равенство угловых скоростей колес
ωкi = ωк = const.

Блокированная трансмиссия
При прямолинейном движении по твердой ОП суммарное сопротивление движению невелико, продольные реакции и моменты на колесах также малы и непосредственное их скольжение отсутствует. В этом случае изменение радиуса качения подчиняется линейному закону
rк = rк0 = rкв – λM Мк = const.
Моменты на колесах определяются выражением:
(*)

Блокированная трансмиссия
Приравняв сумму моментов Mкi к суммарному моменту Mкм, поступающему на колеса КМ, и решив полученное уравнение относительно радиуса качения, имеем
Подставив радиус rк0 в выражение (*), получим формулу для определения крутящего момента j-го колеса при полностью блокированной трансмиссии:

Блокированная трансмиссия
Значения Mкj могут быть положительными (направленными в сторону вращения колес), отрицательными или равными нулю.
При положительном подводимом моменте Mкм > 0 и отрицательных моментах на колесах Mкj < 0 происходит циркуляция крутящего момента (мощности) в замкнутом контуре колесо – ветвь трансмиссии – раздаточная коробка – другие ветви трансмиссии – другие колеса – ОП – колесо.
Без учета потерь циркулирующий момент численно равен крутящим моментам колес, на которых моменты отрицательны. Следовательно, мощность поступает не от трансмиссии к колесам, а наоборот, от колес — в трансмиссию.

Блокированная трансмиссия
Циркуляция мощности – вредное явление, приводящее к дополнительному увеличению нагрузок, потерям в трансмиссии и шинах, и, как следствие, большому износу деталей и узлов, расходу топлива, ухудшению устойчивости движения.
Начало циркуляции момента определяется условием

Блокированная трансмиссия
Вероятность возникновения циркуляции момента (мощности) снижается с уменьшением разности радиусов качения rквi в ведомом режиме, увеличением тангенциальной эластичности λMi, шин и повышением сопротивления движению Mкм.

Вариантов дифференциально-блокированной трансмиссии в многоосных КМ может быть множество в зависимости от числа ведущих осей.
Общую формулу для определения крутящих моментов при всех возможных схемах такой трансмиссии выводить нерационально, поскольку она получается очень громоздкой. Обычно решают частные задачи для конкретных схем.
Смешанная трансмиссия (дифференциально-блокированная)

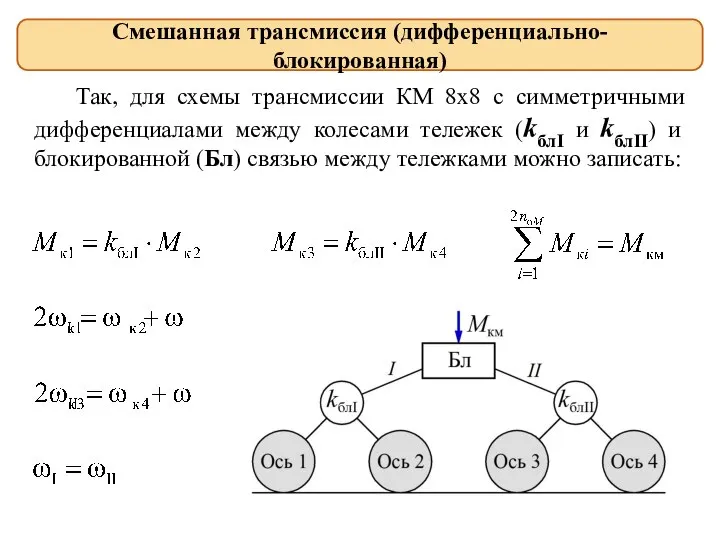
Смешанная трансмиссия (дифференциально-блокированная)
Так, для схемы трансмиссии КМ 8x8 с симметричными дифференциалами между колесами тележек (kблI и kблII) и блокированной (Бл) связью между тележками можно записать: