теория вероятностей

Развитие теории вероятностей с момента зарождения этой науки и до настоящего времени было несколько своеобразным. На первом этапе истории этой науки она рассматривалась как занимательный “пустячок”, как собрание курьезных задач, связанных в первую очередь с азартными играми в кости и карты.

Основателями теории вероятностей были французские математики Б. Паскаль и П. Ферма, и голландский ученый Х. Гюйгенс
Важнейший этап теории вероятностей связан с именем швейцарского математика Я. Бернулли. Им было дано доказательство частного случая закона больших чисел, так называемой теоремы Бернулли.
Строгое логическое обоснование теории вероятностей произошло в XX в. и связано с именами советских математиков С. Н. Бернштейна и А. Н. Колмогорова.
Б. Паскаль
П.Ферма
Х. Гюйгенс
Я. Бернулли
С. Н. Бернштейна
А. Н. Колмогоров

Так, если мы берем идеально изготовленную шестигранную игральную кость, то у нас нет оснований считать, что она на какую-то из граней будет выпадать чаще, чем на другую; более того, есть все основания для того, чтобы считать равновероятным выпадение ее на каждую из граней. Поэтому при бросании такой кости выпадение каждой из них можно ожидать с вероятностью, равной 1/6.
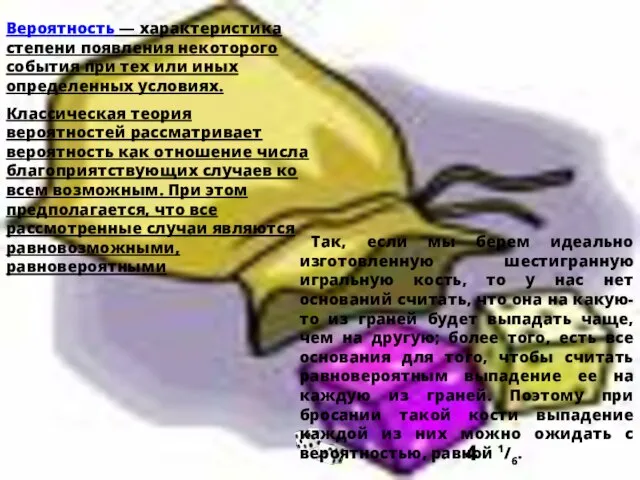
Вероятность — характеристика степени появления некоторого события при тех или иных определенных условиях.
Классическая теория вероятностей рассматривает вероятность как отношение числа благоприятствующих случаев ко всем возможным. При этом предполагается, что все рассмотренные случаи являются равновозможными, равновероятными

Ключевым в частотной теории является понятие относительной частоты. Это отношение числа появлений изучаемого события в серии испытаний в данных условиях к числу всех испытаний, в которых это событие могло бы появиться при тех же условиях. Частотная теория позволяет по результатам относительной частоты изучаемых массовых случайных событий судить об их вероятности.
Применение математики к изучению событий такого характера опирается на то, что во многих случаях при многократном повторении испытаний в примерно равных условиях частота появления результата остается примерно одинаковой. Результат же представляет собой отношение числа опытов, в которых он имел место, к общему числу производимых опытов. Так частота попадания в цель для данного стрелка в одних и тех же условиях при значительном числе испытаний остается почти одной и той же. Процент бракованных изделий в данном ряду испытаний в одном и том же производстве при одинаковых условиях примерно один и тот же.
о частоте событий

Во всех крупных населенных пунктах имеются станции скорой медицинской помощи. Нет возможности заранее предсказать моменты, когда потребуется оказать помощь внезапно заболевшим людям. Как много в течение заданного времени будет вызовов к таким больным? Как долго придется врачу задержаться у больного?
Оказывается, еще в древности люди заметили, что случайное событие — вовсе не исключение в жизни, а правило.
Это явилось объективной предпосылкой для возникновения науки о случайных явлениях. Знать законы случая необходимо. Вот пример.
Сколько врачей и машин необходимо иметь во время дежурства, чтобы, с одной стороны, больные не слишком долго ожидали помощи, а с другой — не наблюдалось бы слишком непродуктивного использования врачебного персонала? Мы сталкиваемся с типичной ситуацией, в которой случайными являются моменты вызовов, длительность пребывания врача у больного, длительность проезда машины от пункта “Скорой помощи” до дома больного… Как видим, неотложная помощь зависит от многих случайных событий. Чтобы помощь была действительно неотложной, надо уметь учитывать все эти случайности.
случайное событие-это правило?

Можно привести и более обыденные примеры. Под потолком висит лампочка — вы не знаете, когда она перегорит. Будет ли завтра снег, никому наверняка неизвестно, даже бюро погоды ошибается. Учитель не знает, сколько ошибок сделает школьник в диктанте.
Теория вероятностей — математическая наука, которая как раз и изучает математические модели случайных явлений, с ее помощью вычисляют вероятности наступления определенных событий Рассмотрим решения нескольких простых задач этой сложной науки.
примеры из жизни

Пусть в урне 7 одинаковых, пронумерованныхшаров.Причем, 1,2,3-черные,остальные-белые. Шарики надо перемешать и вытащить один. Запишите, какого он цвета, и положите шарик обратно. Это первый опыт. Так можно делать много раз подряд. За полчаса можно провести более ста опытов.
Мы хотим предсказать, сколько раз из 100 будет вынут черный шар. Какова его доля во всех опытах? Естественно, каждый раз результат зависит от случая — может попасться черный шар, а может и белый. Но при большом числе опытов примерную долю черных шаров можно предсказать!
Каждый раз вы вынимали из урны либо первый шар, либо второй, … , либо седьмой — всего семь возможных исходов каждого опыта. Шары тщательно перемешаны, на ощупь различить их нельзя, у всех одинаковые шансы быть вынутыми.
Вероятность события =
пример с шарами
Что же можно сказать о черном цвете? Он может в каждом опыте появиться одним из трех способов. Эти исходы называются благоприятными для появления черного шара. Итак, всех опытов — 7, благоприятных исходов — 3, следовательно, в среднем в 3/7 всех опытов вынут черный шар. И чем больше опытов, тем ближе его доля к 3/7.Это и есть вероятность появления черного шара.
Теперь понятно, что каждый шар может появиться в 1/7 части всех опытов, и чем больше раз вы вынимаете шары, тем ближе к 1/7 доля любого из семи исходов. Конечно теоретически можно допустить, что все сто раз вы вынимаете, например, первый шар. Но это совершенно исключительный случай, но мы говорим сейчас о средних результатах.

Эта формула получена с помощью рассуждений. Но соответствуют ли рассуждения действительности? Формулу проверяли ученые на многих опытах, и всегда она получала подтверждение. Доля опытов, в которых событие осуществлялось, была близка к расчетной. Этой формулой пользуются, когда исходы опыта равновозможны и надо только вычислить вероятность.
Опытом или испытанием называют осуществление определенного комплекса условий или действий, при которых происходит соответствующее явление. Возможный результат опыта называют событием. Например, опытом является подбрасывание монеты, а событиями — “герб” или “цифра” на верхней стороне после падения монеты. Опытами являются стрельба по мишени, извлечение шара из ящика, бросание игрального кубика и т. д.
формула теории вероятностей

Достоверным называют событие, которое обязательно произойдет в данном опыте. Например, если в ящике находятся только красные шары, то событие из ящика извлечен красный шар является достоверным (в ящике нет шаров другого цвета).
Невозможным называется событие, которое не может произойти в этом опыте. В нашем примере таковым является событие из ящика извлечен синий шар (таких шаров просто нет).
Случайным называется событие, если оно может произойти, а может и не произойти в данном опыте. Если бы в урне находились красные и синие шары, то событие из ящика извлечен красный шар — случайное (ведь мы можем и не извлечь красный шар в данном испытании). Случайными событиями являются “герб” и цифра на верхней стороне монеты при ее подбрасывании, выигрыш по билету лотереи и т. п.
Два события называются совместными в данном опыте, если появление одного из них не исключает появления другого в этом же опыте. Так, при подбрасывании двух монет события A — “герб на верхней стороне первой монеты” и B — “цифра на верхней стороне второй монеты являются совместными.
Равновозможными считают события, если нет оснований полагать, что одно событие является более возможным, чем другие. Например, при подбрасывании монеты событие K (появление цифры) и событие L (появление герба) равновозможными. Такими же являются появления любой из шести граней при подбрасывании игрального кубика.
Каждое событие, которое может наступить в итоге опыта, называется элементарным исходом (элементарным событием или шансом). Например, события A1, A2, A3, A­4, A5, A6 — элементарные исходы при подбрасывании кубика.
Элементарные исходы, при которых данное событие наступает, называются благоприятствующими этому событию, или благоприятными шансами. Например, при подбрасывании игрального кубика элементарные исходы A2, A­4, A6 являются благоприятствующими событию “выпало четное число очков”.
классификация событий

Элементы теории вероятностей на уроках математики
Первый шаг на пути ознакомления школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при одних и тех же условиях, а детям предлагают указать результат. Потом условия эксперимента изменяют.
1.

Задача 1
Эксперимент, помогающий подвести школьников к понятиям: невозможное событие, достоверное событие, а в отношении случайных событий — установить градации: более вероятное событие, менее вероятное событие.
Оборудование: мешок и 9 шаров — 3 красных, 3 белых и 3 зеленых.
Описание эксперимента. Учитель обращается к ребятам:
— Вы, конечно, знаете, что Буратино очень любит кукольные спектакли, но у него часто не бывает денег, чтобы попасть в театр. Однажды продавец билетов согласился дать Буратино билет, если он верно ответит на вопрос: “В мешке имеется 3 красных, 3 белых и 3 зеленых шара. Сколько шаров нужно вынуть из мешка, чтобы наверняка иметь шары трех цветов?” Помогите Буратино дать правильный ответ.
Дети будут предлагать разные значения, но им необходимо обосновать свой выбор, проводя эксперименты. В результате они должны прийти к следующим выводам:
— если вынуть 7, 8, 9 шаров, наверняка будут шары трех цветов;
— если вынуть 3, 4, 5 или 6 шаров, то возможно, но не обязательно будут шары трех цветов;
— если вынуть 1 или 2 шара, то невозможно получить шары трех цветов.
Целесообразно исследовать, в каком из случаев имеется наибольшая возможность получить шары трех цветов — если вытащить 3, или 4, или 5, или 6 шаров. Можно ввести и термины более вероятно, менее вероятно
приложение
пять задач

. С помощью этих экспериментов можно научить ребенка навыку выводить закономерности при проведении опытов.
Оборудование: 5 одинаковых монет.
Описание эксперимента. Учитель рассказывает детям следующую историю:
— Когда Буратино получил от Карабаса-Барабаса 5 золотых монет, он подбросил каждую монету, чтобы удостовериться, не сон ли это, и не исчезнут ли золотые. Буратино видел, что каждая монета ложилась одним из возможных способов: цифрой вверх или гербом вверх. Потом он подбросил все 5 монет сразу и подсчитал, что 2 монеты легли цифрой вверх, а 3 гербом. Буратино задумался: какие случаи еще могут получиться? Давайте поможем Буратино.
В этом и заключается задание: отметить, какие случаи возможны при бросании пяти монет. Занести данные в таблицу и заполнить ее, написав свое предположение о количестве появления каждого случая. Сравнить полученное число с результатами эксперимента, проведенного 20, 40, 60, 80 и 100 раз.
Задача 2. Опыты с пятью монетами.

Эксперимент, который можно использовать при знакомстве с понятиями: равновозможные события, более вероятное событие, менее вероятное событие.
Оборудование: два белых и один черный шар.
Описание эксперимента. В ящик или мешок кладут два белых и один черный шар. Требуется вытащить последовательно один за другим 2 шара. Учитель спрашивает детей: “Каким может быть результат такого опыта?”
Обнаруживается, что может быть 3 случая:
С помощью эксперимента необходимо выяснить, какой из этих случаев более возможен, менее возможен или, может быть, среди них имеются равновозможные случаи. Затем полученные экспериментальные выводы необходимо обосновать, рассмотрев все возможные комбинации выбора двух шаров из имеющихся трех, которые можно условно обозначить Ч, Б1, Б2.
Задача 3.

Задача 4. Игра “Какова сумма?” Эта игра поможет подвести
К понятию вероятности с точки зрения классического определения.
Нарисуем большой прямоугольник, 1411 клеток. Между 14 детьми распределим 14 жетонов, пронумерованных от 1 до 14. Дети ставят свои домики на линию старта на клетку с соответствующим номером. Бросаем две большие игральные кости. После каждого подбрасывания костей ребенок, номер которого равен сумме очков на выпавших гранях продвигается на одну клетку к финишу. Выигрывает тот, кто первым достигнет финиша.
Очень скоро дети догадываются, что некоторые из них находятся в более благоприятных условиях, чем другие, и что участники, получившие номера 1, 13, 14 не имеют никакого шанса продвинуться вперед (имея две кости, невозможно в сумме получить 1 или число, большее 12). Тогда дети решают, что в следующей партии эти числа надо выбросить. Можно сыграть несколько партий. Дети хотят получить номер 5, 6, 7, 8, 9, но никто не хочет взять 2, 3, 4, 10, 11 или 12. Разумно попробовать обосновать, почему так происходит, попросив детей ответить на вопрос, сколькими способами можно получить 2, 3, 4,..., 12 очков при бросании двух игральных костей.
Задача 4.

Игра “Сколько окажется на своем месте?” Эта игра помогает на интуитивном уровне подвести детей к понятию относительной частоты.
Надо вырезать из картона 5 одинаковых карточек, написав на них цифры от 1 до 5, затем перетасовать их и выложить на стол в той последовательности, в которой они оказались после перетасовывания, например, в такой:
При этом только одна цифра — 5 — соответствует номеру места, на котором она лежит.
Далее можно сформулировать серию вопросов, на которые дети должны ответить на основании данных, полученных в ходе экспериментов. Такими вопросами могут быть:
1) Как вы думаете, насколько редким является исход
2) Будет ли еще более редкий случай, когда ни одна карточка не окажется на своем месте?
3) Будет ли случай, когда все карточки лежат на своем месте?
4) Что можно сказать о частоте исхода, когда две (три, четыре) цифры окажутся на своем месте?
Эксперименты можно вести в следующем направлении: провести опыты 10 раз; результаты занести в таблицу и вычислить значение относительной частоты по каждому вопросу при n = 10.
Затем повторить опыт еще 10 раз. На самом деле мы имеем уже 20 опытов, которые опять заносим в таблицу и вычисляем относительную частоту при n = 20. Проделав опыт, например, 100 раз, можно определить приближенное значение вероятности для каждого исхода
Задача 5.