Триангуляция неявно заданных поверхностей

ННГУ, ВМК, 2005 г
Тестирование GridBean API
План презентации
О чем поговорим?
Постановка задачи
Алгоритм решения
Реализация
Демонстрация
Выводы

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Постановка задачи
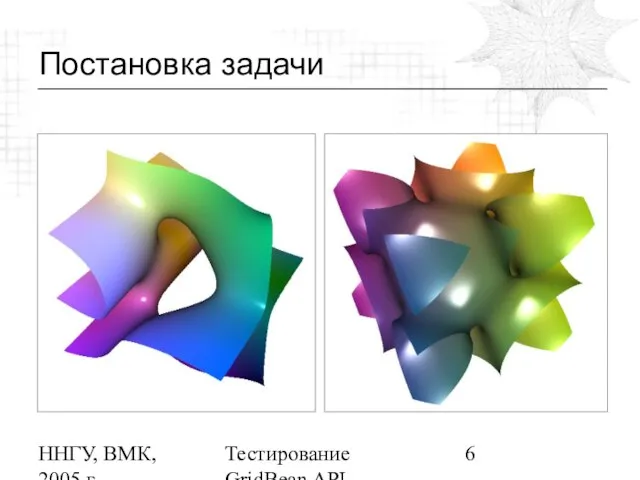
Определение
Неявно заданной поверхностью называется множество точек трехмерного пространства, отвечающих уравнению
F(x, y, z) = C,
где C есть некоторое постоянное число
Примеры
x2 + y2 + z2 = 9
x2 + y2 - z2 = 0
sin(x) - cos(y) - cos(z) = 0

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Постановка задачи
Постановка задачи
Постановка
Требуется построить поверхность, отвечающую уравнению F(x, y, z) = C,
где C есть некоторое постоянное число.
Уравнение предполагается заданным в прямоугольной системе координат. Задаются границы параллелепипеда, в котором строится поверхность, а также строка, содержащая уравнение. Результатом работы программы является изображение поверхности, выполненное средствами какой-либо графической библиотеки.

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Постановка задачи
Постановка задачи
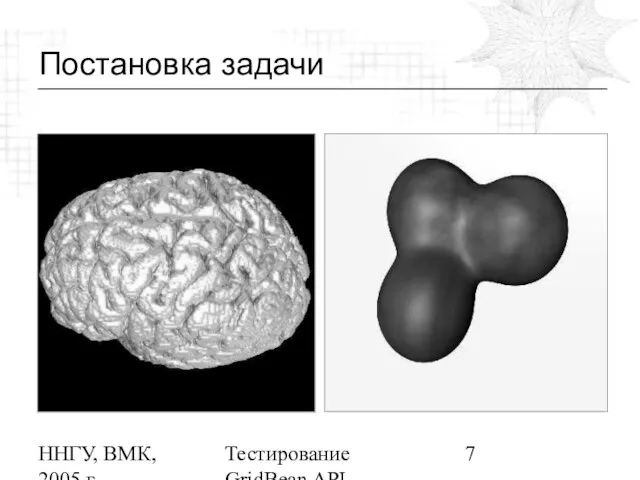
Где мы встречаемся с этим Трехмерные поверхности часто встречаются в медицине. Так что алгоритм MC часто используется для представления различных медицинских данных
Различные разделы математики и физики, а также других точных наук, где изучается распределение некоторой характеристики процесса в трехмерном пространстве
Топография, трехмерное представление рельефа местности, моделирование

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Постановка задачи

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Постановка задачи

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Постановка задачи
Алгоритм марширующих кубов
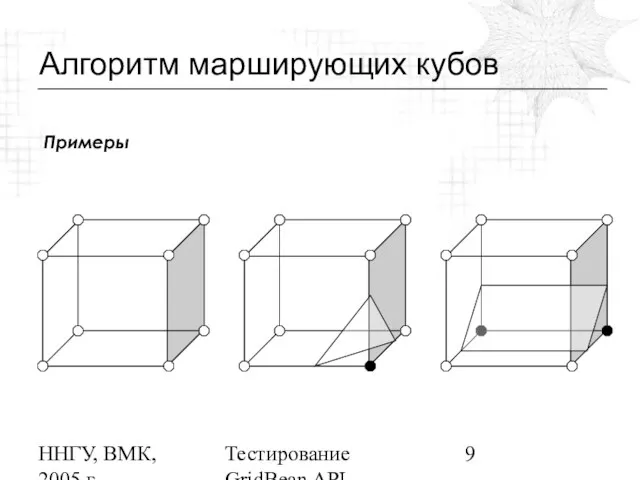
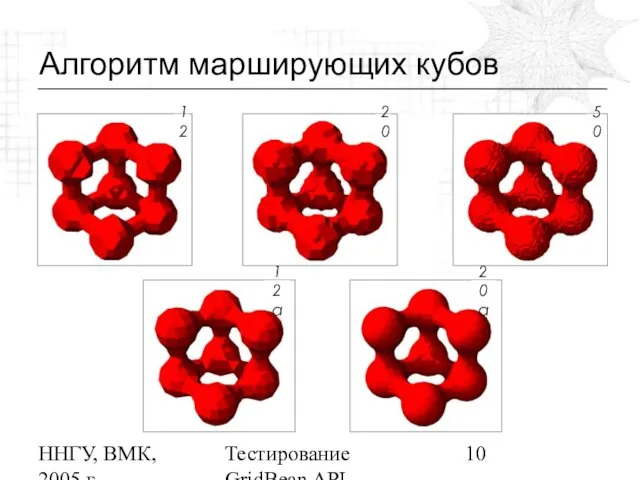
Алгоритм MC
Область разбивается на кубики. Вычисляются значения функции в каждой вершине вокселя и сравнивается с нулем.
Если на концах ребра функция имеет различные знаки, то поверхность пересекает это ребро. Просмотрев все ребра каждого вокселя, определить способ аппроксимации

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Постановка задачи
Алгоритм марширующих кубов
Примеры

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Алгоритм марширующих кубов
12
20
50
12a
20a

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Реализация алгоритма

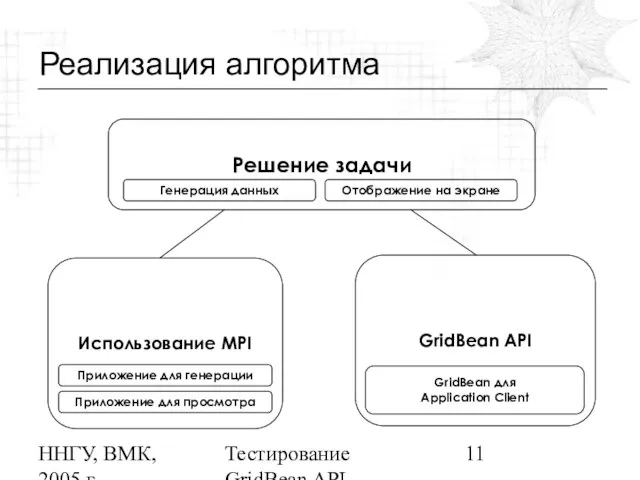
ННГУ, ВМК, 2005 г
Тестирование GridBean API
Описание задания
Описание Grid-задания
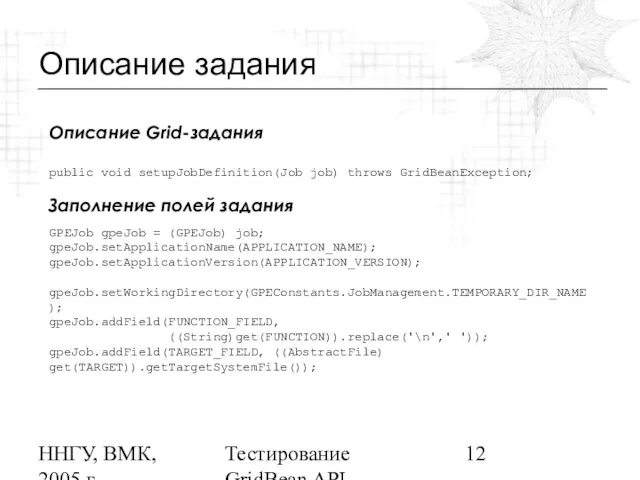
public void setupJobDefinition(Job job) throws GridBeanException;
Заполнение полей задания
GPEJob gpeJob = (GPEJob) job;
gpeJob.setApplicationName(APPLICATION_NAME);
gpeJob.setApplicationVersion(APPLICATION_VERSION);
gpeJob.setWorkingDirectory(GPEConstants.JobManagement.TEMPORARY_DIR_NAME);
gpeJob.addField(FUNCTION_FIELD,
((String)get(FUNCTION)).replace('\n',' '));
gpeJob.addField(TARGET_FIELD, ((AbstractFile) get(TARGET)).getTargetSystemFile());

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Реализация алгоритма
Спецификация выходных параметров
SurfaceBuilder генерирует два файла. Первый файл содержит грубую модель поверхности, второй точную и требующую больше времени на прорисовку
public GridBeanParameter[] getOutputParameters()
{
GPEFile[] files = getFiles();
GridBeanParameter[] parameters = new GridBeanParameter[files.length];
for (int i = 0; i < files.length; i++)
{
QName paramName = QNameUtil.derive(TARGET, "file" + i);
parameters[i] = new GridBeanParameter(paramName,
GridBeanParameterType.GPE_FILE);
set(paramName, files[i]);
}
return parameters;
}

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Построение пользовательского интерфейса
При создании элементов управления на панели ввода или вывода необходимо:
связать элемент управления с некоторым именем
JTextField funcTextField = new JTextField();
add(new JLabel("Function:"), LayoutTools.makegbc(0, 1, 1, 1,false));
add(funcTextField, LayoutTools.makegbc(1, 1, 5, 100, true));
linkTextField(GraphGridBean.FUNCTION, funcTextField);
задать процедуру валидации введенного значения
setValueValidator(GraphGridBean.FUNCTION,
NotNullValidator.getInstance());
задать процедуру преобразования значения, введенного в элемент управления, во внутреннее представление
setValueTranslator(GraphGridBean.FUNCTION,
StringValueTranslator.getInstance());
задать описание элемента управления
setDescription(GraphGridBean.FUNCTION, "Function");

ННГУ, ВМК, 2005 г
Тестирование GridBean API
Выводы
Преимущества GridBean
Удобство использования. Пользователь работает с «одной» программой, а не с двумя отдельными
Кроссплатформенность. Не требуется даже перекомпиляции исходных текстов программы, в отличие от программ, написанных на Си/Си++.
Доступ к программе из любой точки мира. Требуется лишь загрузить компактный GridBean
Единые принципы работы с различными GridBean’ами
Приложение работает в распределенной среде, получая, таким образом, доступ к почти неограниченным вычислительным ресурсам