Слайд 2Определение тригонометрии
Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника.

Слайд 3История тригонометрии
Тригонометрия возникла из практических нужд человека. С ее помощью можно определить

расстояние до недоступных предметов и, вообще, существенно упрощать процесс геодезической съемки местности для составления географических карт.
Слайд 4История тригонометрии
Зачатки тригонометрических познаний зародились в древности. На раннем этапе тригонометрия развивалась

в тесной связи с астрономией и являлась ее вспомогательным разделом.
Слайд 6 Окончательный вид тригонометрия приобрела в XVIII веке в трудах Л. Эйлера.
Леонард

Эйлер
Слайд 7Дороги не те знания, которые откладываются в мозгу, как жир, дороги те,

которые превращаются в умственные мышцы.
Слайд 8Арксинус и его свойства
Арксинусом числа a (|a|≤1) называется такой угол α, принадлежащий

отрезку
[-π/2; π/2], синус которого равен a.
Обозначается этот угол arcsin a. Читается так: угол, синус которого равен a .
Слайд 9Арккосинус и его свойства
Арккосинусом числа a (|a|≤1) называется такой угол α, принадлежащий

отрезку [0; π], косинус которого равен a.
Обозначается этот угол arccos a. Читается так: угол, косинус которого равен a .
Слайд 10Арктангенс и его свойства
Арктангенсом числа a называется такой угол α, принадлежащий интервалу

(-, )тангенс которого равен a.
Обозначается этот угол arctg a. Читается так: угол, тангенс которого равен a .
Слайд 12Мне приходится делить время между политикой и уравнениями. Однако уравнения, по –

моему, гораздо важнее. Политика существует только данного момента, а уравнения будут существовать вечно.
Слайд 13Решение простейших тригонометрических уравнений вида:
, где

Слайд 15Решение простейших тригонометрических уравнений вида:
, где

Слайд 17Решение простейших тригонометрических уравнений вида:


















 «Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами»
«Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами» Роспись петуха по мотивам Филимоновской росписи
Роспись петуха по мотивам Филимоновской росписи Гражданское право. Понятие и виды сроков в гражданском праве
Гражданское право. Понятие и виды сроков в гражданском праве Модернизм
Модернизм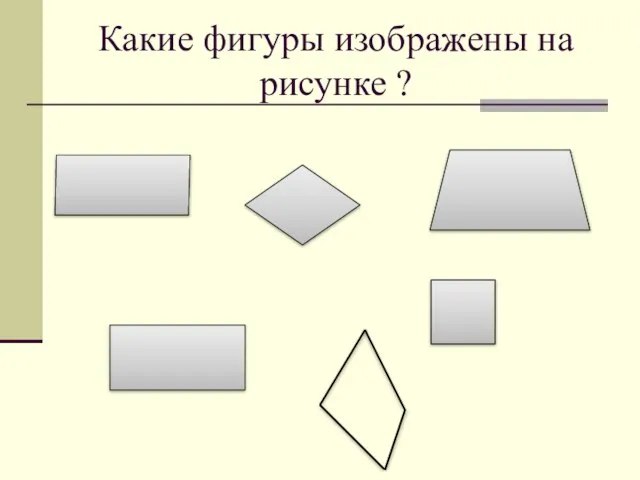 Какие фигуры изображены на рисунке ?
Какие фигуры изображены на рисунке ? Перенос слова переносятся по слогам
Перенос слова переносятся по слогам Принтеры
Принтеры Методическая разработка «Создание презентаций» Элективный курс для 10 класса.
Методическая разработка «Создание презентаций» Элективный курс для 10 класса. Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне
Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне Федеральное Собрание РФ
Федеральное Собрание РФ Инжиниринг нефтехимии и нефтегазопереработки
Инжиниринг нефтехимии и нефтегазопереработки Китайский клуб МИИТа
Китайский клуб МИИТа Мой город, с тебя начинается Родина (город Сатка)
Мой город, с тебя начинается Родина (город Сатка) Спартакиада пенсионеров муниципального образования Город Гатчина
Спартакиада пенсионеров муниципального образования Город Гатчина Эры. Основные события органического мира
Эры. Основные события органического мира Презентация на тему Операционные системы на мобильных устройствах
Презентация на тему Операционные системы на мобильных устройствах  Живопись
Живопись Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы
Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70
Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70 МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942)
МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942) Векторы в пространстве и не только
Векторы в пространстве и не только Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники Трансформация изображения через трансформацию формы - серия открыток
Трансформация изображения через трансформацию формы - серия открыток ОРНАМЕНТЫ в национальном костюме
ОРНАМЕНТЫ в национальном костюме Цветник для солнечного места “Степной бриз ”
Цветник для солнечного места “Степной бриз ” Презентация на тему Тургенев. Стихи в прозе
Презентация на тему Тургенев. Стихи в прозе 287 Воскресшему служу я
287 Воскресшему служу я Берлину заменить Северный поток-2 другим проектом
Берлину заменить Северный поток-2 другим проектом