Тригонометрия в географии!!!

С помощью тригонометрии в нашей жизни можно всё измерить и вычислить даже не имея под рукой никаких формул,приборов и таблиц!!!
А сейчас мы попробуем определить величину угла без измерений и многое другое…..

ЗАДАЧА 1:определение величины данного угла без всяких измерений!!!
Для измерения углов на местности нам нужен компас или достаточно собственных пальцев. А если надо измерить угол нанесённый на карту или бумагу, и под рукой не будет транспортира???

РЕШЕНИЕ:
Из вершины О,как из центра,произвольным раствором булавки построим окружность.
Точки C и D её пересечения со сторонами угла соединим отрезком прямой.
Теперь от точки C на окружности откладываем при помощи булавки хорду CD в одном и том же направлении до тех пор, пока ножка булавки опять совпадёт с точкой C.
Откладывая хорды, мы считаем сколько раз за это время будет обойдена окружность и сколько раз будет отложена хорда.
Допустим, что окружность мы обошли n раз и за это время S раз отложили хорду CD.Тогда искомый угол будет равен:
∠ AOB=360*n/S

ЗАДАЧА 2:найти углы треугольного участка!!!
Во время экскурсии мы измерили шагами стороны треугольного участка и нашли, что они равны 43, 60 и 54 шагам. Каковы углы этого треугольника???

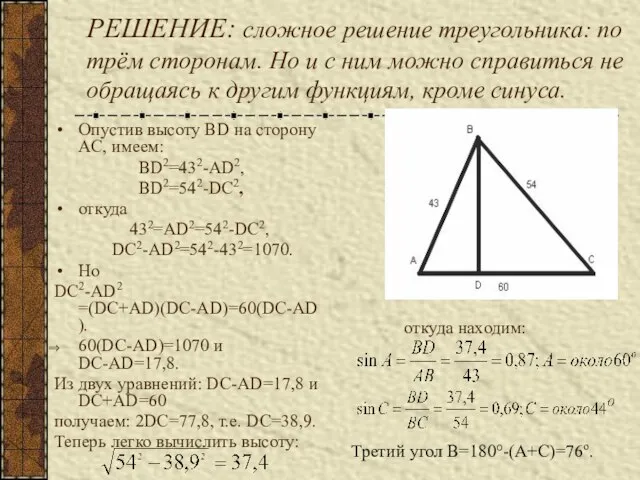
РЕШЕНИЕ: сложное решение треугольника: по трём сторонам. Но и с ним можно справиться не обращаясь к другим функциям, кроме синуса.
Опустив высоту BD на сторону AC, имеем:
BD2=432-AD2,
BD2=542-DC2,
откуда
432=AD2=542-DC2,
DC2-AD2=542-432=1070.
Но
DC2-AD2 =(DC+AD)(DC-AD)=60(DC-AD).
60(DC-AD)=1070 и DC-AD=17,8.
Из двух уравнений: DC-AD=17,8 и DC+AD=60
получаем: 2DC=77,8, т.е. DC=38,9.
Теперь легко вычислить высоту:
откуда находим:
Третий угол B=180°-(A+C)=76о.

Чему же равны синусы различных углов от 1о до 90о?
Как узнать это, не имея под рукой таблиц??? Весьма просто: надо составить таблицу синусов самому. Этим мы сейчас и займемся.
Начнём с тех углов, синусы которых нам известны из геометрии.
Это прежде всего, угол в 90о,синус которого равен 1. Затем угол в 45о,синус которого легко вычислить по теореме Пифагора; он равен т.е. 0,707.
Далее нам известен синус 30о. Так как катет, лежащий против такого угла, равен половине гипотенузы, то sin30о=1/2.

Итак, мы знаем синусы(или, как принято обозначать, sin) трёх углов:
SIN 30о=0,5,
SIN 45о=0,707,
SIN 90о=1.
Например, для угла в 1о дуга
и,следовательно,sin 1о
можно принять равным
Таким же образом находим:
SIN 2О
SIN
SIN
SIN
SIN 2о=0,0349,
SIN 3о=0,0524,
SIN 4о=0,0698,
SIN 5о=0,0873.

Синусы от 15 до 30о мы вычислим с помощью пропорций.
sin 30о-sin 15о=0,50-0,26=0,24
При увеличении угла на каждый градус синус его возрастает примерно на этой разницы, т.е. на
Итак, прибавляя последовательно по 0,016 к sin 15о, получим синусы 16о,17о,18о и т.д. :
sin 16о=0,26+0,016=0,28,
sin 17о=0,26+0,032=0,29,……………

Так же вычисляем углы от 30одо 45о!!!
sin 45о-sin 30о=0,707-0,5=
=0,207
Разделив её на 15,имеем 0,014.
sin 31°=0,5+0,014=0,514,
sin 32°=0,5+0,028=0,528,
……………………….......

Найдем синусы острых углов больше 45 о с помощью теоремы Пифагора.
Например, найдём
Т.к. B=37о, то sin 37о=
=0,5+7*0,014=0,598.
Зная, что ,
значит AC=0,6*AB. Получаем:

Вывод исследования тригонометрии в географии:
Тригонометрия очень нужна в географии, с помощью знаний тригонометрии можно измерить ширину реки и высоту дерева. Тригонометрия позволяет нам самим составить таблицы и расчитать по ним всё что нам нужно!!!