Учебно-исследовательская работа «Многогранники»

Введение
При исследовании многогранников перед собой мы поставили следующие задачи:
Изучить разновидности многогранников.
Научиться строить некоторые модели многогранников.
Исследовать вращающие кольца тетраэдров.

Многогранники
С древнейших времен наши представления о красоте связаны с симметрией. Наверное, этим объясняется интерес человека к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей.

Многогранник
Это пространственное тело с плоскими гранями и прямолинейными ребрами, устроенное так, чтобы всякое ребро соединяет две вершины и служит общей стороной двух граней

Простейшими примерами многогранников служат пирамиды и призмы
У пятиугольной призмы:
10 вершин
15 ребер
7 граней
У пятиугольной пирамиды:
6 вершин
10 ребер
6 граней

Антипризма (призмоид)
Основания одинаковые, но расположены различно: вершины каждого из оснований лежат над сторонами другого, так что боковые ребра идут зигзагом
У пятиугольной антипризмы:
10 вершин
20 ребер
12 граней

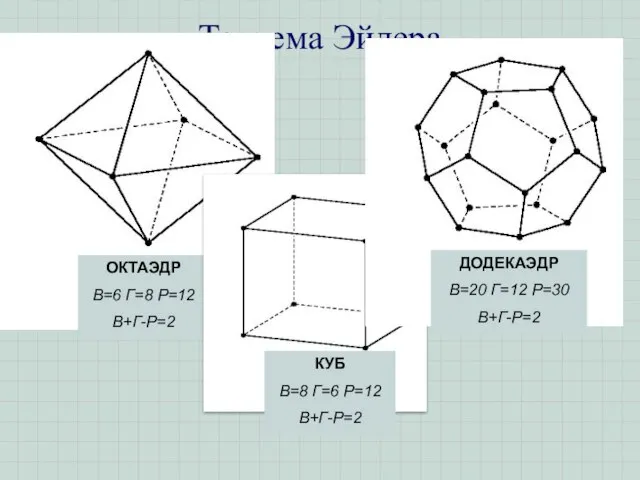
Для любого выпуклого многогранника справедливо соотношение
Г+В-Р=2
Г- число граней,
В- число вершин,
Р- число ребер данного многогранника
Теорема Эйлера

Теорема Эйлера

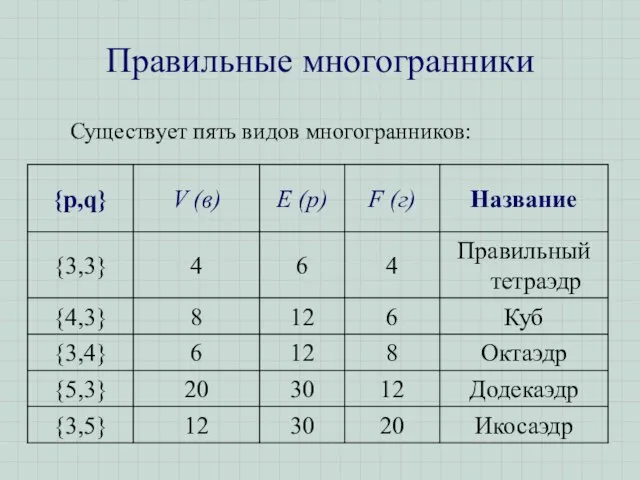
Правильные многогранники
Существует пять видов многогранников:

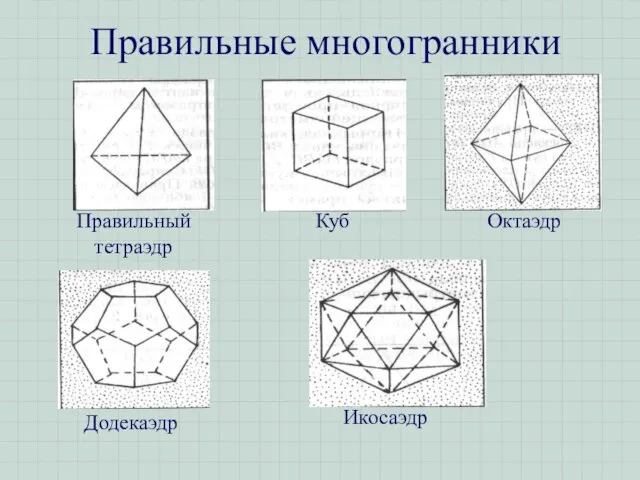
Правильные многогранники

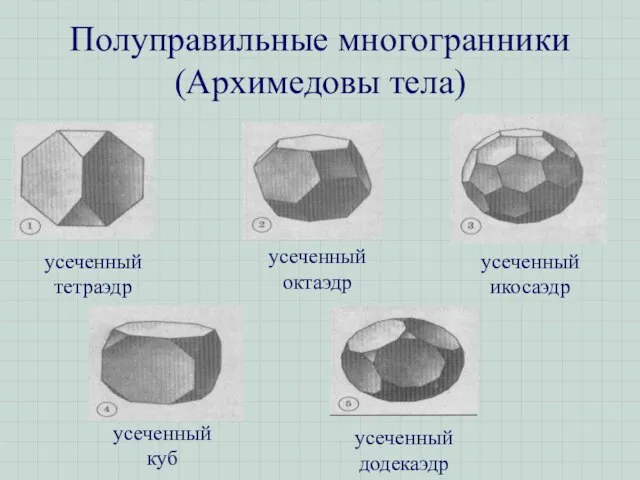
Полуправильные многогранники
(Архимедовы тела)

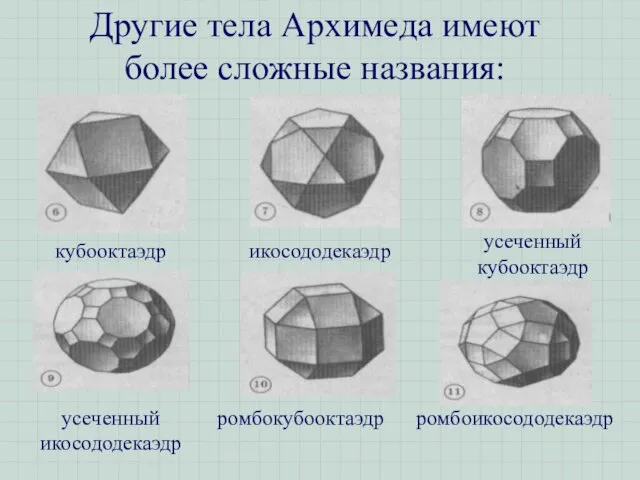
Другие тела Архимеда имеют более сложные названия:

Вращающие кольца тетраэдров
Дж. М. Андреас и Р. М. Сталкер независимо друг от друга открыли семейство изгибаемых конечных многогранников с 2n вершинами, 6n ребрами и 4n треугольными гранями. Гранями служат грани n тетраэдров, соединенных между собой в циклическом порядке по определенным парам противоположных ребер каждого, так что получается фигура наподобие кольца.

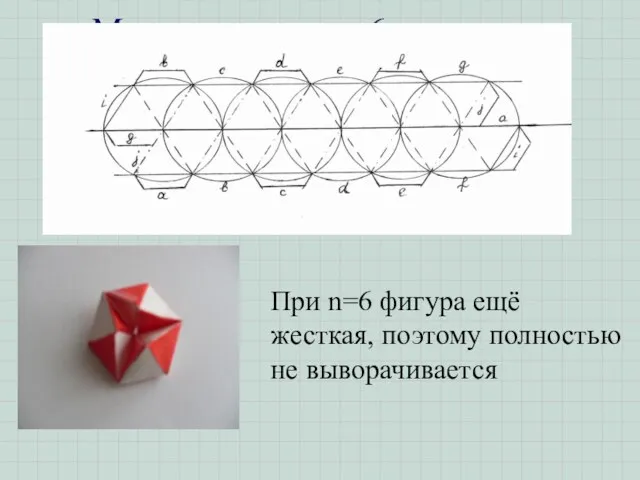
Модель кольца из 6 тетраэдров
При n=6 фигура ещё жесткая, поэтому полностью не выворачивается

Модель кольца из 8 тетраэдров

Заключение:
Проводя исследования по данной теме, мы изучили исторические данные по многогранникам;
При построении разверток многогранников мы научились работать с чертежными инструментами;
Создавая модели призмы, антипризмы, пирамиды, а также вращающих колец из тетраэдров мы расширили свое пространственное воображение.
В дальнейшей работе мы хотим научиться строить модели более сложных по виду многогранников.