Содержание
- 2. Системы счисления. Логические основы ЭВМ Лекция 2
- 3. Системы счисления. Логические основы ЭВМ Системы счисления, определения Позиционные СС Непозиционные СС Логические основы ЭВМ Логические
- 4. Определения Система счисления – это способ записи чисел с помощью специальных знаков – цифр. Числа: 123,
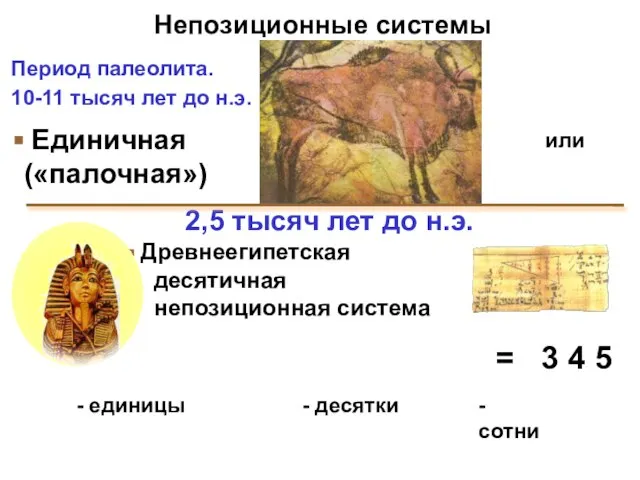
- 5. Единичная («палочная») Период палеолита. 10-11 тысяч лет до н.э. 2,5 тысяч лет до н.э. Древнеегипетская десятичная
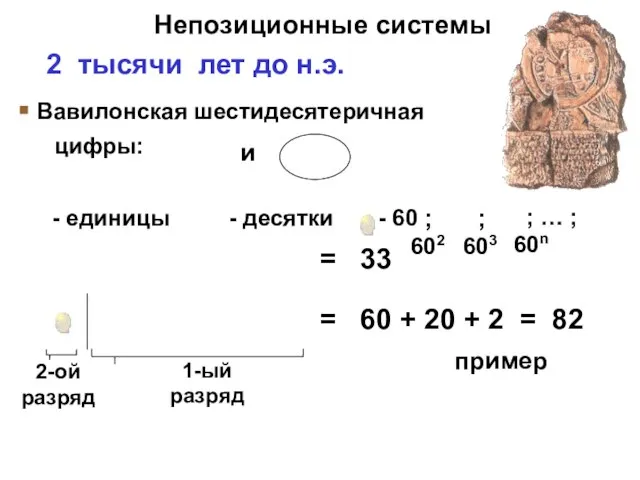
- 6. 2 тысячи лет до н.э. Вавилонская шестидесятеричная - единицы - десятки = 33 цифры: и -
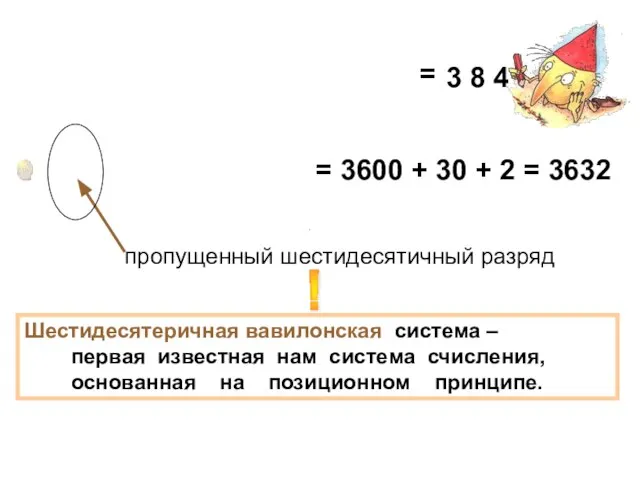
- 7. 3 8 4 пропущенный шестидесятичный разряд = 3600 + 30 + 2 = 3632 Шестидесятеричная вавилонская
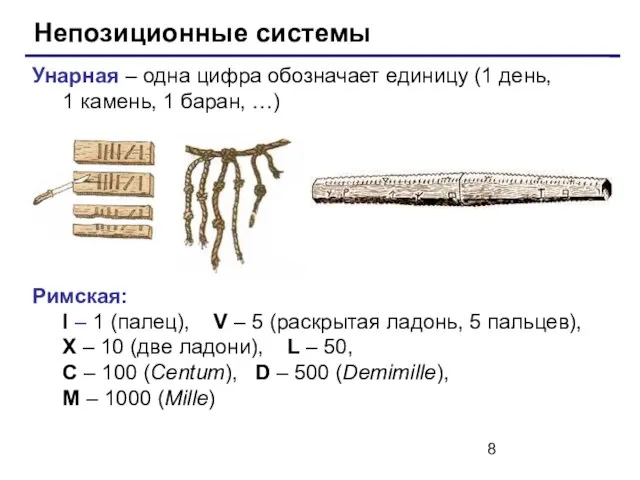
- 8. Непозиционные системы Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …) Римская:
- 9. Римская система счисления Правила: (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только
- 10. Римская система счисления Недостатки: для записи больших чисел (>3999) надо вводить новые знаки-цифры (V, X, L,
- 11. Славянская система счисления алфавитная система счисления (непозиционная)
- 12. Позиционные системы Позиционная система: значение цифры определяется ее позицией в записи числа. Десятичная система: первоначально –
- 13. Системы счисления. Логические основы ЭВМ Двоичная система счисления
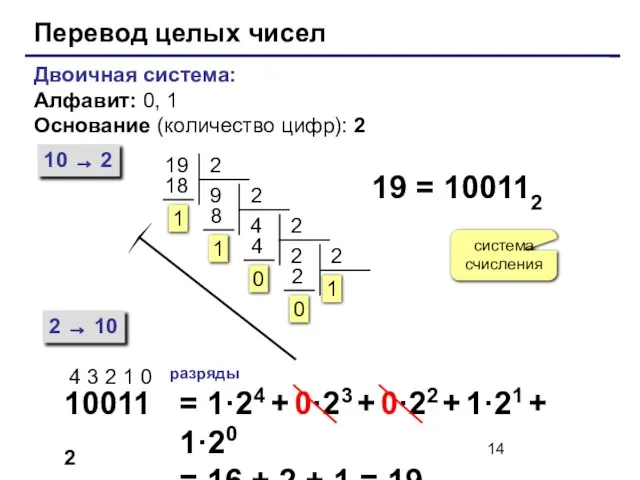
- 14. Перевод целых чисел Двоичная система: Алфавит: 0, 1 Основание (количество цифр): 2 10 → 2 2
- 15. Примеры (2 варианта, решить самостоятельно): 131 = 79 = 1010112 = 1101102 =
- 16. Перевод дробных чисел 10 → 2 2 → 10 0,375 = × 2 101,0112 2 1
- 17. Примеры (по 1 на каждый вариант): 0,625 = 3,875 =
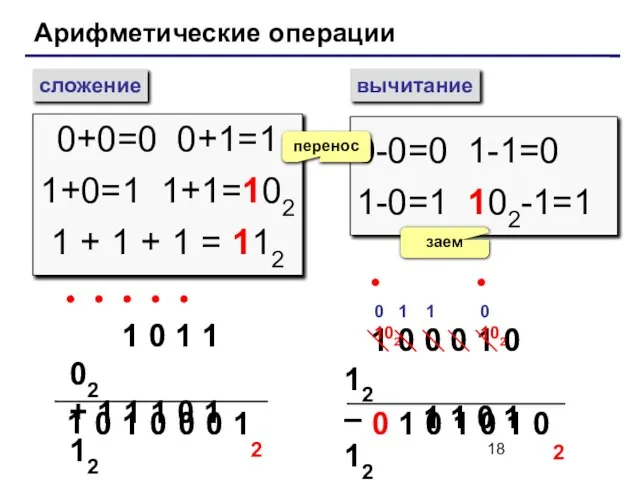
- 18. Арифметические операции сложение вычитание 0+0=0 0+1=1 1+0=1 1+1=102 1 + 1 + 1 = 112 0-0=0
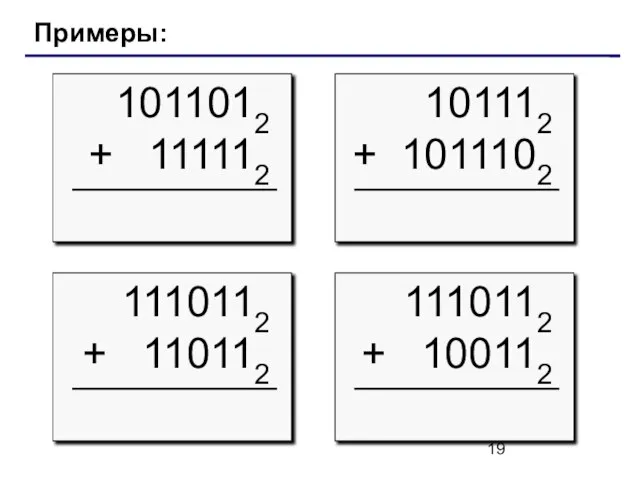
- 19. Примеры:
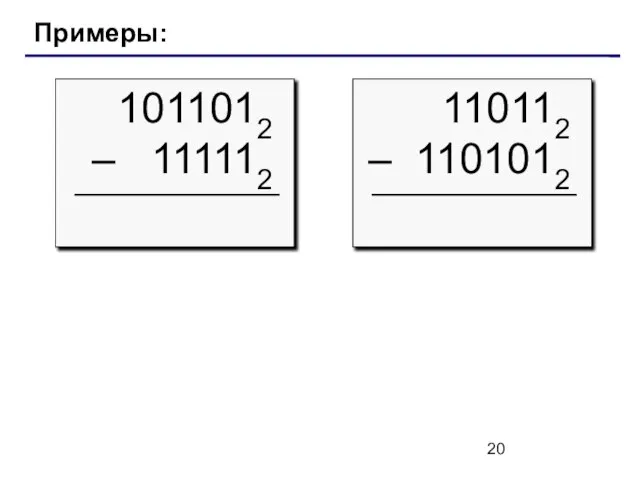
- 20. Примеры:
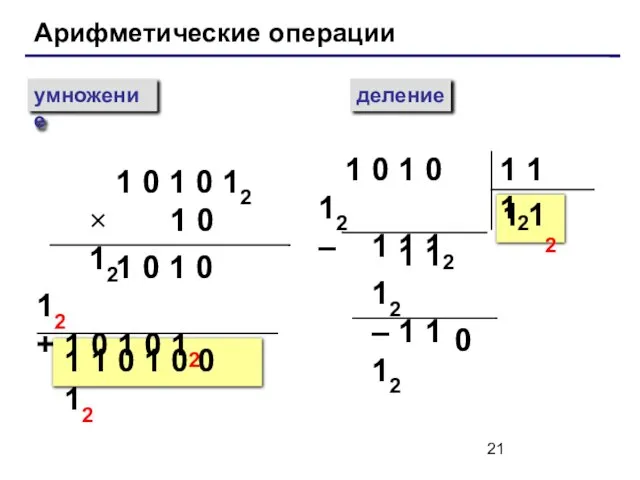
- 21. Арифметические операции умножение деление 1 0 1 0 12 × 1 0 12 1 0 1
- 22. Плюсы и минусы двоичной системы нужны технические устройства только с двумя устойчивыми состояниями (есть ток —
- 23. Системы счисления. Логические основы ЭВМ Восьмеричная система счисления
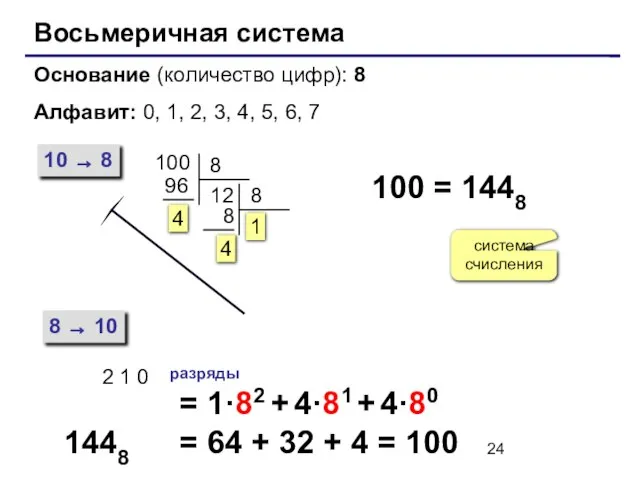
- 24. Восьмеричная система Основание (количество цифр): 8 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7 10
- 25. Примеры: 134 = 75 = 1348 = 758 =
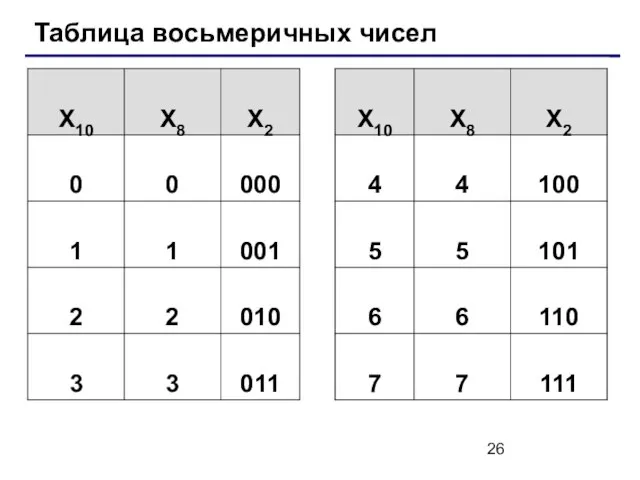
- 26. Таблица восьмеричных чисел
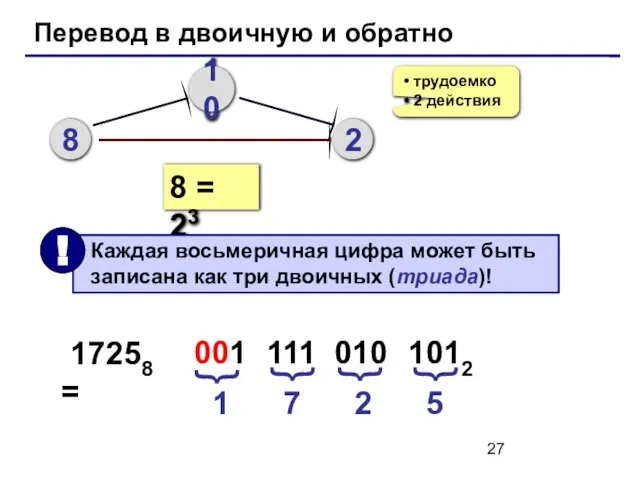
- 27. Перевод в двоичную и обратно 8 10 2 трудоемко 2 действия 8 = 23 17258 =
- 28. Примеры: 34678 = 21488 = 73528 =
- 29. Перевод из двоичной системы 10010111011112 Шаг 1. Разбить на триады, начиная справа: 001 001 011 101
- 30. Примеры: 1011010100102 = 111111010112 = 11010110102 =
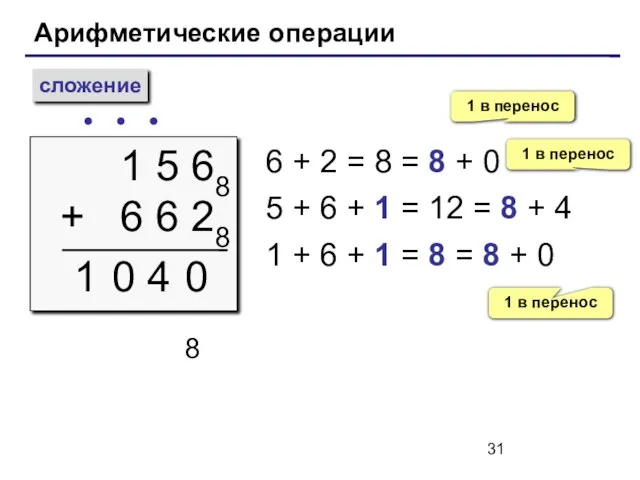
- 31. Арифметические операции сложение 1 5 68 + 6 6 28 ∙ 1 6 + 2 =
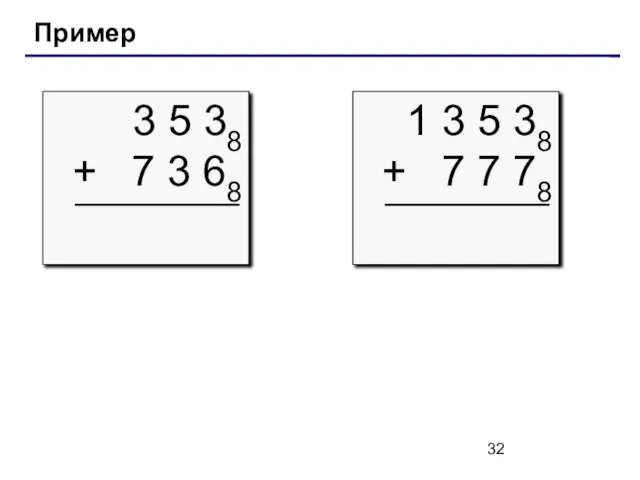
- 32. Пример
- 33. Арифметические операции вычитание 4 5 68 – 2 7 78 ∙ (6 + 8) – 7
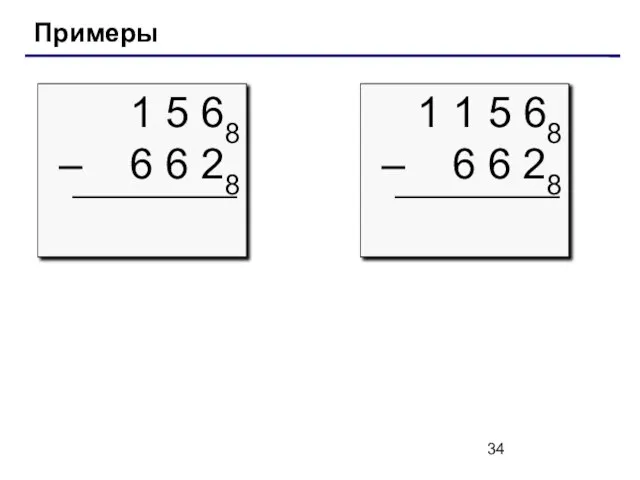
- 34. Примеры
- 35. Системы счисления. Логические основы ЭВМ Шестнадцатиричная система счисления
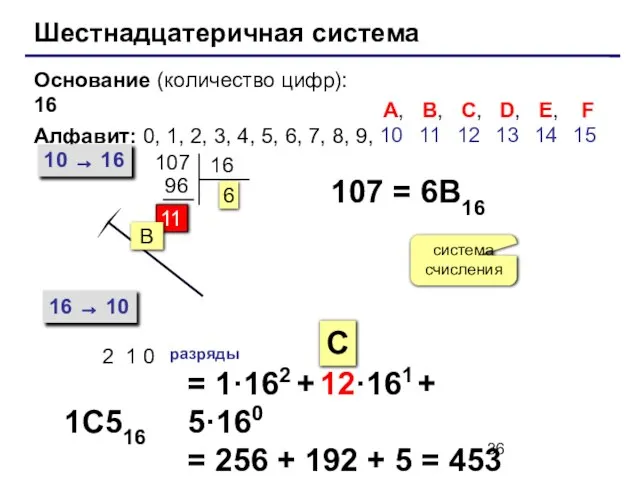
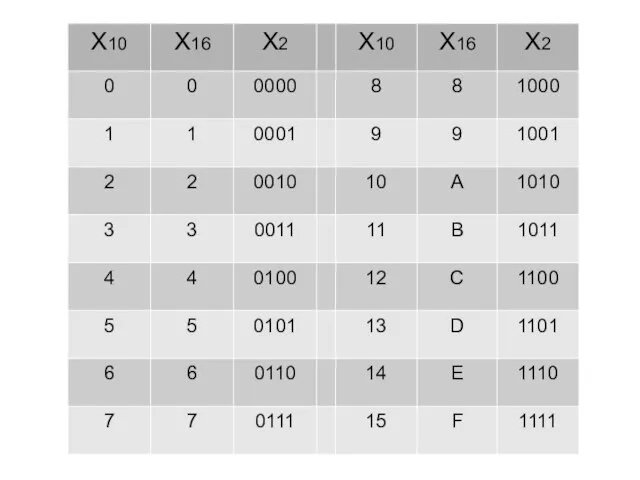
- 36. Шестнадцатеричная система Основание (количество цифр): 16 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8,
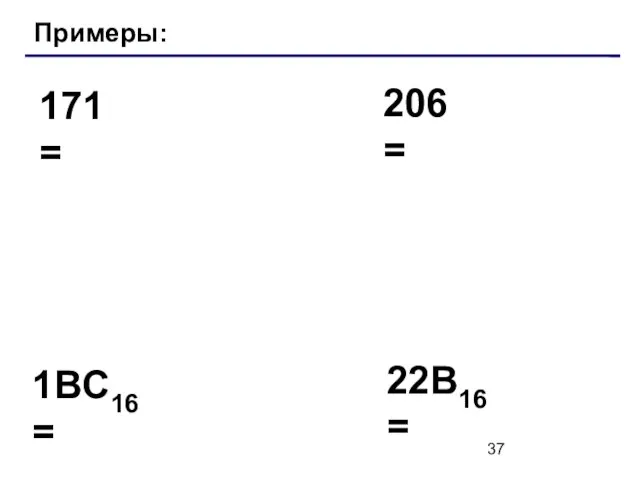
- 37. Примеры: 171 = 206 = 1BC16 = 22B16 =
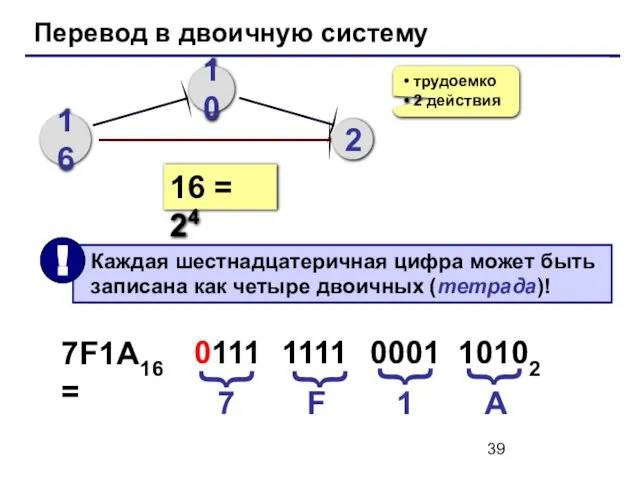
- 39. Перевод в двоичную систему 16 10 2 трудоемко 2 действия 16 = 24 7F1A16 = 7
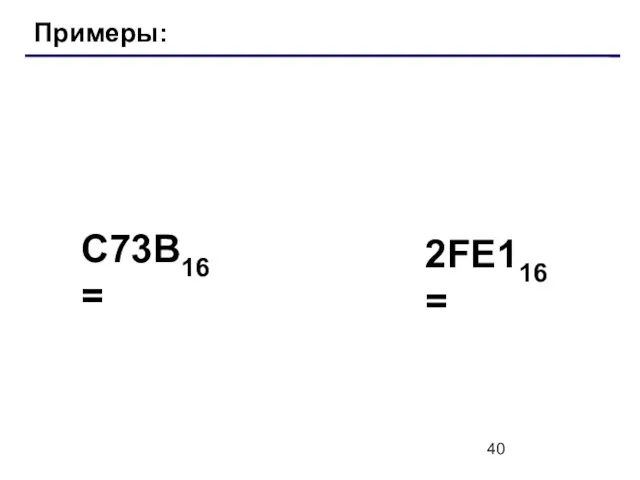
- 40. Примеры: C73B16 = 2FE116 =
- 41. Перевод из двоичной системы 10010111011112 Шаг 1. Разбить на тетрады, начиная справа: 0001 0010 1110 11112
- 42. Примеры: 10101011010101102 = 1111001101111101012 = 1101101101011111102 =
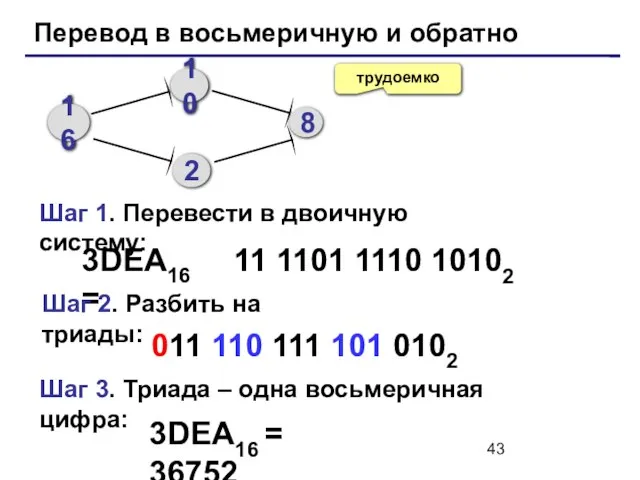
- 43. Перевод в восьмеричную и обратно трудоемко 3DEA16 = 11 1101 1110 10102 16 10 8 2
- 44. Примеры: A3516 = 7658 =
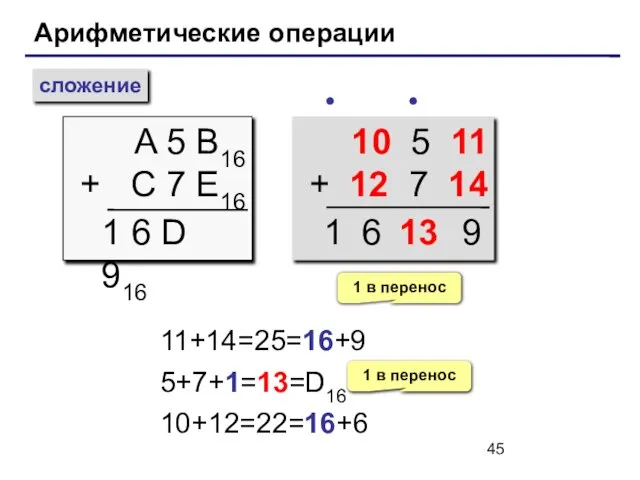
- 45. Арифметические операции сложение A 5 B16 + C 7 E16 ∙ 1 6 D 916 10
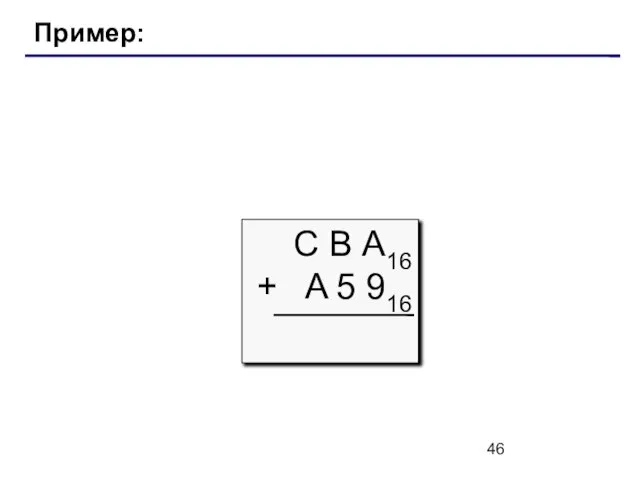
- 46. Пример: С В А16 + A 5 916
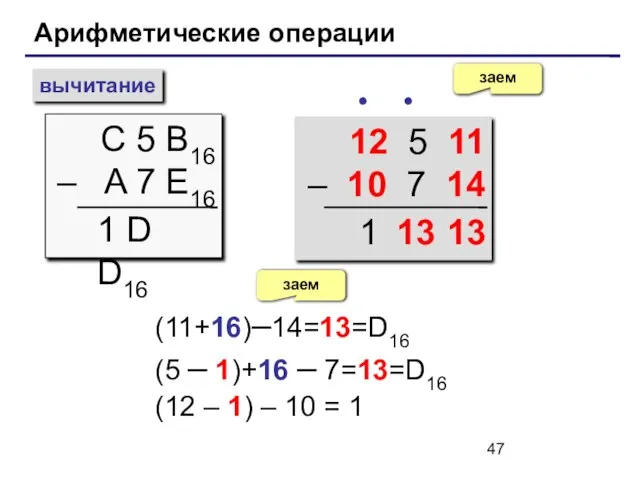
- 47. Арифметические операции вычитание С 5 B16 – A 7 E16 заем ∙ 1 D D16 12
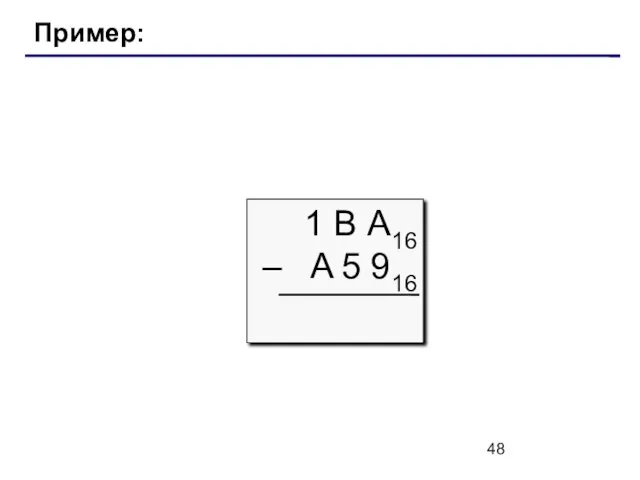
- 48. Пример: 1 В А16 – A 5 916
- 49. «ЛОМАЕМ» голову стихотворение А.Н.Старикова: Ей было 1100 лет, Она в 101-й класс ходила, В портфеле по
- 50. «ЛОМАЕМ» голову Шел Кондрат В Ленинград, А навстречу – 1100 ребят. У каждого по 11 лукошек,
- 51. «ЛОМАЕМ» голову 10 ног на 11 ногах, А 100 в зубах. Вдруг 100 прибежали И с
- 52. Пословицы и поговорки с использованием СС Конь о 100 ногах и тот спотыкается. У 111 мамок
- 53. Пословицы и поговорки с использованием СС Добрый друг лучше 1100100 родственников. С одного вола, 10 шкур
- 54. Системы счисления. Логические основы ЭВМ Другие системы счисления
- 55. Троичная уравновешенная система Задача Баше: Найти такой набор из 4 гирь, чтобы с их помощью на
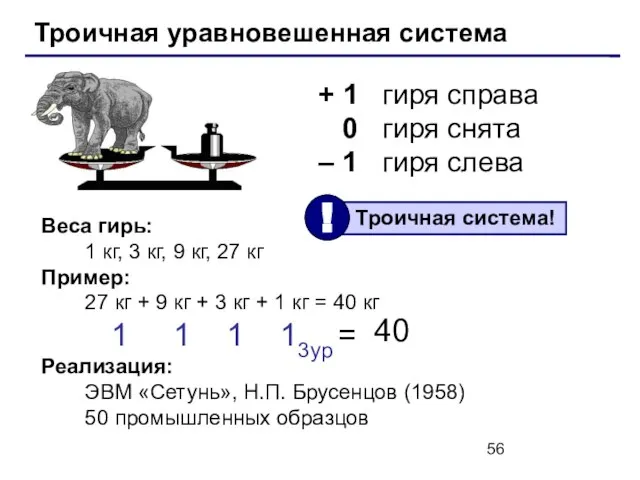
- 56. Троичная уравновешенная система + 1 гиря справа 0 гиря снята – 1 гиря слева Веса гирь:
- 57. Системы счисления. Логические основы ЭВМ Логические основы ЭВМ
- 58. Логические основы ЭВМ Принципы работы ЭВМ основываются на законах математической логики, поэтому ее элементы широко используются
- 59. Понятие имеет две характеристики: 1) содержание; 2) объем. Содержание понятия – это совокупность существенных признаков, выделяющих
- 60. Высказывание (суждение, утверждение) – это повествовательное предложение, в котором утверждаются или отрицаются свойства реальных предметов и
- 61. Умозаключение позволяет из известных фактов (истинных высказываний) получать новые факты. Например, из факта «Все углы треугольника
- 62. Системы счисления. Логические основы ЭВМ Логические операции
- 63. Основные логические операции над высказываниями, используемыми в ЭВМ, включают отрицание, конъюнкцию, дизъюнкции, стрелку Пирса и штрих
- 64. 4. Стрелка Пирса X ↓ Y. Стрелка Пирса X ↓ Y (NOR (NOT OR), ИЛИ-НЕ) –
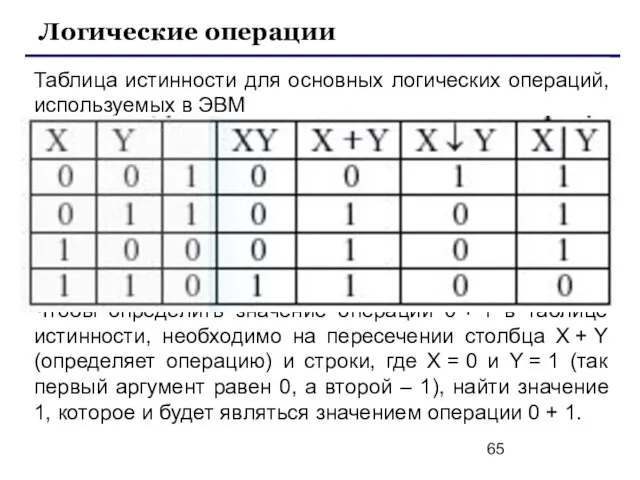
- 65. Таблица истинности для основных логических операций, используемых в ЭВМ Чтобы определить значение операции 0 + 1
- 67. Скачать презентацию





































 Формирование национальной стратегии работы по обеспечению успешной социализации воспитанников интернатных учреждений в Республ
Формирование национальной стратегии работы по обеспечению успешной социализации воспитанников интернатных учреждений в Республ Парк Лефортово
Парк Лефортово ПСК. Лекция 2_Психологические основы коммуникации
ПСК. Лекция 2_Психологические основы коммуникации Конкурс молодых специалистов с инвалидностью Путь к карьере
Конкурс молодых специалистов с инвалидностью Путь к карьере Правовой фундамент государства
Правовой фундамент государства Земля Луна
Земля Луна Власть и общество в России: развитие взаимодействия и повышение эффективности гражданского участия
Власть и общество в России: развитие взаимодействия и повышение эффективности гражданского участия Ключевое преимущество программы Kempinski Discovery
Ключевое преимущество программы Kempinski Discovery Система классификации горнолыжных трасс
Система классификации горнолыжных трасс Инновационная образовательная программа московского городского психолого-педагогического университета
Инновационная образовательная программа московского городского психолого-педагогического университета Презентация на тему "Роль классного руководителя по формированию ученического коллектива в 5-м классе" - скачать презентации
Презентация на тему "Роль классного руководителя по формированию ученического коллектива в 5-м классе" - скачать презентации  Транспортный налог
Транспортный налог Проверка домашнего задания.
Проверка домашнего задания. Учебное пособие для студентов педагогических учебных заведений Педагогика как любовь
Учебное пособие для студентов педагогических учебных заведений Педагогика как любовь Презентация ОСО. Объединенный совет обучающихся ВГЛТУ
Презентация ОСО. Объединенный совет обучающихся ВГЛТУ Презентация на тему Самоиндукция
Презентация на тему Самоиндукция 2012г.
2012г. Классическая противомикробная терапия предполагает: этиотропность лечения: выбор и назначениеантибиотиков в соот
Классическая противомикробная терапия предполагает: этиотропность лечения: выбор и назначениеантибиотиков в соот Книжная печатная графика
Книжная печатная графика Рефлексия на уроках русского языка и литературы
Рефлексия на уроках русского языка и литературы Сущность биосоциальной природы психики и поведения человека
Сущность биосоциальной природы психики и поведения человека Инструменты анализа ключевых слов для западной аудитории
Инструменты анализа ключевых слов для западной аудитории Договор подряда
Договор подряда  Погода 6 класс
Погода 6 класс Секция маркетинговых исследователей Украинского Маркетинг Клуба MarketingJazzz Методы маркетинговых исследований в рознице: преимущ
Секция маркетинговых исследователей Украинского Маркетинг Клуба MarketingJazzz Методы маркетинговых исследований в рознице: преимущ Мышцы
Мышцы Организация обучения в рамках программы «Школа по уходу»
Организация обучения в рамках программы «Школа по уходу» Презентация на тему 26 ноября – Всемирный день информации
Презентация на тему 26 ноября – Всемирный день информации