Улитка Паскаля

Содержание
1). Этьен Паскаль.
2). Улитка Паскаля (или лимакона).
3). Трисекция угла.
4). Кардиоида.
5). Эффекты с кривыми.
6). Создание шедевров.
7). Список использованной литературы, INTERNET-ресурс.

Паскаль.(19.06.1623-19.08.1662)
Французский математик, физик и философ. В 1641 сконструировал суммирующую машину. К 1645 закончил ряд работ по арифметике, теории чисел, алгебре и теории вероятностей, опубликованную в 1665. Паскаль нашел общий признак делимости любого целого числа на любое другое целое число; дал способ нахождения числа сочетаний из n по m; сформулировал ряд основных положений элементарной теории вероятностей. Труды Паскаля, связанные с циклоидой, явились существенным шагом в развитии анализа бесконечно малых.
В 1625 Этьен Паскаль в своей переписке с Мерсенном, у которого частенько собирались за чашкой чая знаменитые геометры, в том числе и Gilles-Personne Roberval, описал метод построения новой кривой, обладающей интересными свойствами ( которую впоследствии назвали Улиткой).

Улитка Паскаля.
Улитка Паскаля – плоская алгебраическая кривая 4-го порядка. Уравнение в прямоугольных координатах:
(x²+y²-ax)²=l²(x²+y²);
В полярных координатах: P=a cos φ + l;
Симметрична относительно оси ох. Площадь, ограниченная улиткой паскаля:
S=+πL²;
Из начала координат проведен луч, пересекающий данную окружность x²+y²=2x (а›0) в точке В; на луче по обе стороны от точки В отложены равные между собой отрезки ВМ и ВN постоянной длины b. При вращении луча точки M и N описывают кривую, называемую улиткой Паскаля.

Трисекция угла с помощью улитки Паскаля
Опишем метод деления произвольного угла на три равные части с помощью кривой, названной улиткой Паскаля.
Для построения улитки Паскаля достаточно нарисовать окружность W произвольного радиуса R = a, выбрать на ней некоторую точку А и начать вращать вокруг точки А луч АС. Если по обе стороны от второй точки пересечения луча АС с окружностью на луче АС откладывать отрезки, равные радиусу исходной окружности ( R = a), то получится два набора точек - М и М'. Улитка Паскаля - геометрическое место точек М и М'. Для завершения построения через полученные точки достаточно провести плавную непрерывную линию.

Выполним трисекцию произвольного угла с помощью улитки Паскаля
Пусть требуется разделить на три равные части данный угол KLN. Для этого вычерченная на кальке улитка Паскаля накладывается на угол KLN таким образом, чтобы центр образующей окружности совпал с вершиной угла, а ось улитки АА' - совпала со стороной угла KLN. Точку Д ( точку пересечения угла с улиткой) соединим с точкой А. Тогда угол AДL будет искомым, то есть угол AДL = 1\3 угла KLN.
Доказательство:
соединим точку В ( в которой образующая окружность пересекает АД ) с точкой С.
Треугольники ABL и LBД - равнобедренные, так как АL = LB = BД = а. Угол BDL = x следовательно, угол BLД = x , таким образом получаем, что угол ABL = 2x, следовательно, угол BAL = 2x.
Отсюда угол KLN = угол Д + угол BAL = x+2x.
Получаем : Х = 1\3 угла KLN.

Кардиоида (Cardioid)
Если использовать две окружности с
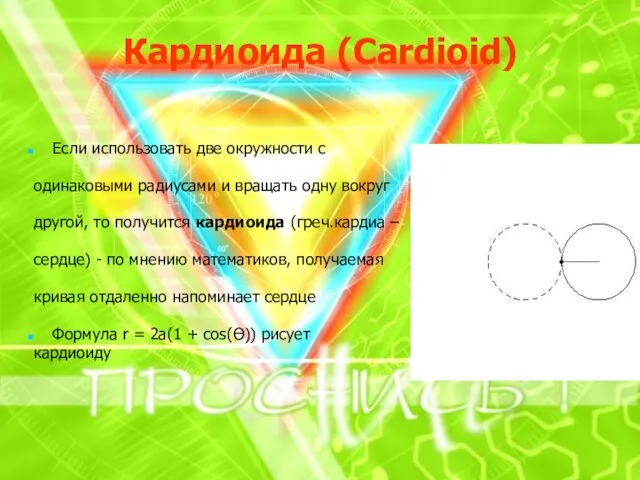
одинаковыми радиусами и вращать одну вокруг другой, то получится кардиоида (греч.кардиа –
сердце) - по мнению математиков, получаемая
кривая отдаленно напоминает сердце
Формула r = 2a(1 + cos(Ө)) рисует
кардиоиду

Эффекты с кривыми
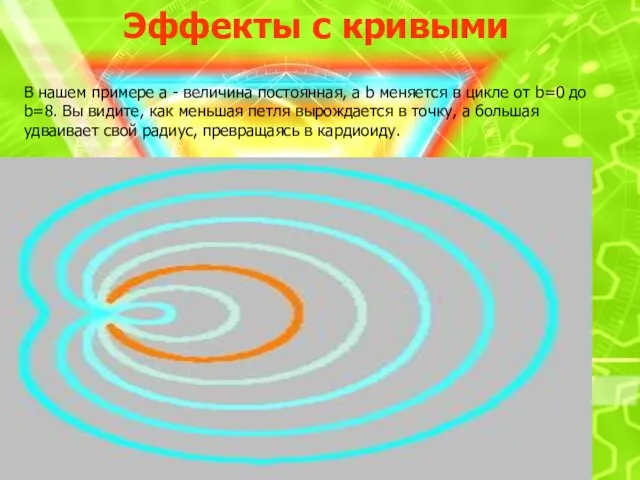
В нашем примере a - величина постоянная, а b меняется в цикле от b=0 до b=8. Вы видите, как меньшая петля вырождается в точку, а большая удваивает свой радиус, превращаясь в кардиоиду.

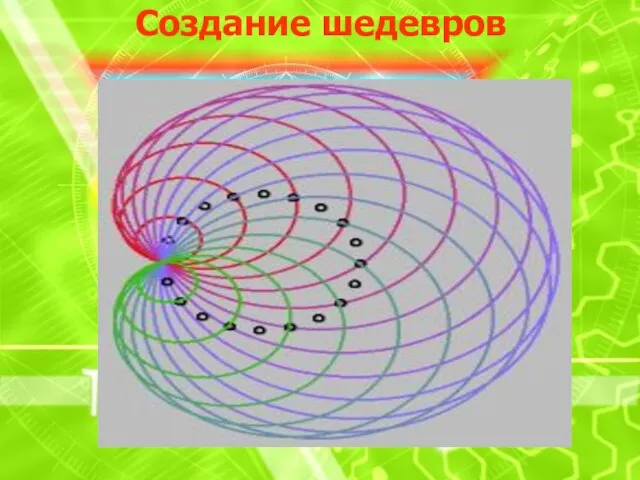
Создание шедевров

Теперь нас отделяет от создания шедевра один маленький шаг делаем толщину линии побольше (например, 55 пикселей) и раскрашиваем каждый четный круг в желтый цвет, а нечетный в черный. И получаем шедевр поп-арта, которому позавидовал бы сам Малевич.

Паутина
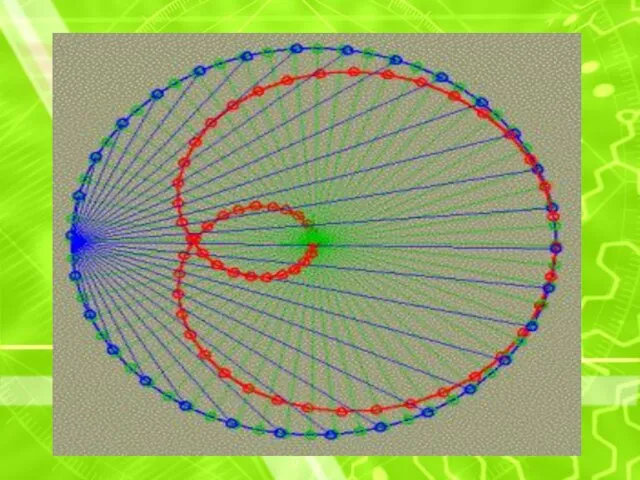
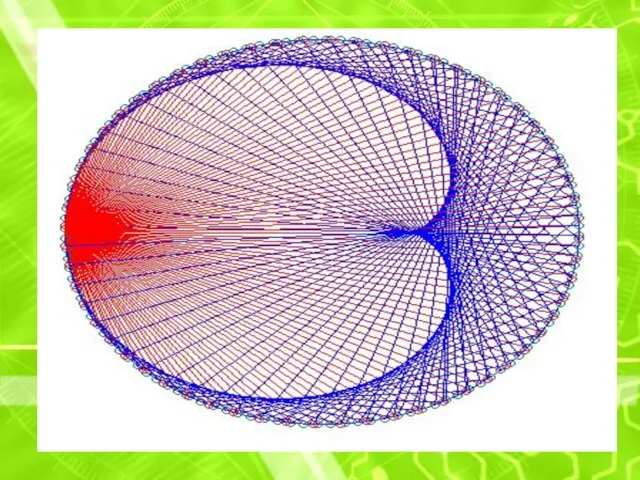
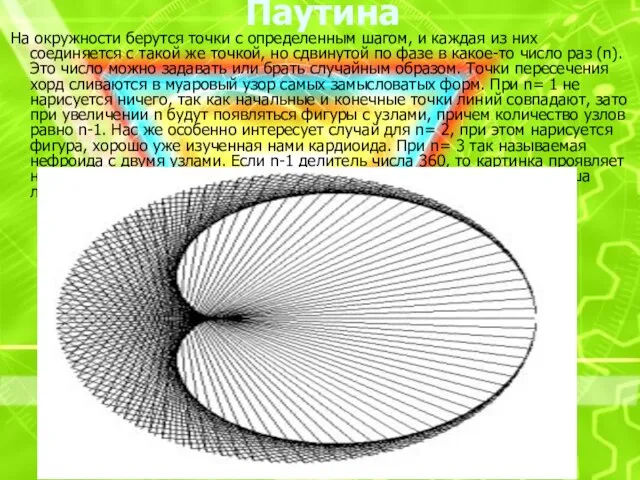
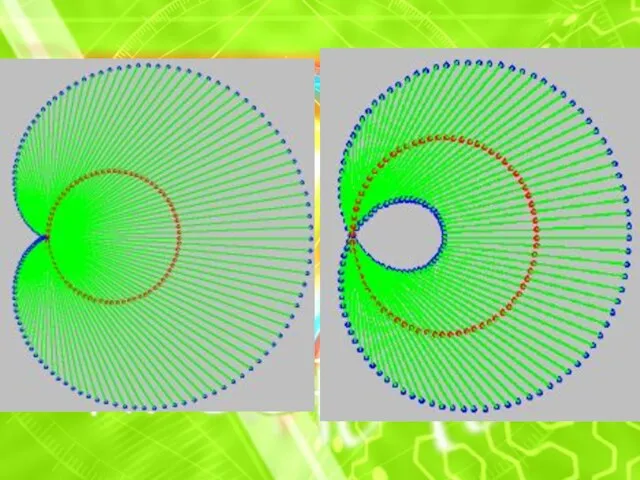
На окружности берутся точки с определенным шагом, и каждая из них соединяется с такой же точкой, но сдвинутой по фазе в какое-то число раз (n). Это число можно задавать или брать случайным образом. Точки пересечения хорд сливаются в муаровый узор самых замысловатых форм. При n= 1 не нарисуется ничего, так как начальные и конечные точки линий совпадают, зато при увеличении n будут появляться фигуры с узлами, причем количество узлов равно n-1. Нас же особенно интересует случай для n= 2, при этом нарисуется фигура, хорошо уже изученная нами кардиоида. При n= 3 так называемая нефроида с двумя узлами. Если n-1 делитель числа 360, то картинка проявляет некоторую упорядоченность. Приводим картинки для значений n= 2 (наша любимая кардиоида)