Управление запасами в логистике. Определение величины страхового запаса

ЗАДАНИЕ 1. ОПРЕДЕЛИТЬ ВЕЛИЧИНУ СТРАХОВОГО ЗАПАСА
Исходные данные: потребность в заказываемом продукте в течение года 1000 ед.; оптимальный размер заказа Qo=
Периодичность выполнения заказов Т=
Средний расход запаса в день равен:
На предприятии были собраны данные о фактическом расходе и реальных сроках поставки партий. В результате статистической обработки были определены средние квадратические отклонения ежедневного расхода и времени поставки .
Порядок решения:
По формуле Феттера-Даллека определяется СКО для страхового запаса:
Допустим, что вероятность отсутствия дефицита Р=0,95, т.е. коэффициент . Определим размер страхового запаса:
2

ЗАДАНИЕ 2. ОПРЕДЕЛЕНИЕ ТЕКУЩЕГО И СТРАХОВОГО ЗАПАСА ПРИ РАЗНЫХ ЗАКОНАХ РАСПРЕДЕЛЕНИЯ
Исходные данные: Обработав данные о фактическом расходе, на предприятии получили сведения, что ежедневный расход запаса подчиняется нормальному закону с параметрами: среднее значение =3 ед., среднее квадратическое отклонение ; время поставки подчиняется распределению Пуассона с параметром Т=5 дн. Допустим, что случайная величина расхода Q подчиняется нормальному закону, вероятность отсутствия страхового запаса Р=0,95 и коэффициент .
3

ПОРЯДОК РЕШЕНИЯ
4
Определить величину текущего запаса:
= =
Определить СКО для страхового запаса с учетом распределения Пуассона:
= =
Определить величину страхового запаса:
Уточним закон распределения случайной величины Q с помощью коэффициента вариации:
Величина коэффициента вариации для положительных случайных величин Q говорит о том, что вместо нормального закона следует использовать другой закон распределения, например, Релея. Определим параметр распределения исходя из следующего:
, отсюда
, отсюда

ПОРЯДОК РЕШЕНИЯ
5
Возьмем среднее значение
Если подчиняется распределению Релея, расчетная формула для величины страхового запаса в виде

ЗАДАНИЕ 3. ОПРЕДЕЛЕНИЕ СТРАХОВОГО ЗАПАСА В СООТВЕТСТВИИ С ВЕРОЯТНОСТНО-ЭКОНОМИЧЕСКОЙ МОДЕЛЬЮ
Исходные данные: Специалист по управлению запасами имеет следующие данные: потребность в продукте А=1200 ед., оптимальная партия поставки =100 ед.; затраты на хранение единицы продукта сх=50 руб./ед.год; потери из-за дефицита оцениваются в размере сд=100 руб/ед.год; =20 ед. Специалист рассчитал, что страховой запас должен быть Qс=21 ед.
Задание: Каковы будут затраты, связанные со страховым запасом? Правильно, с точки зрения минимума затрат, специалист определил размер страхового запаса?
6

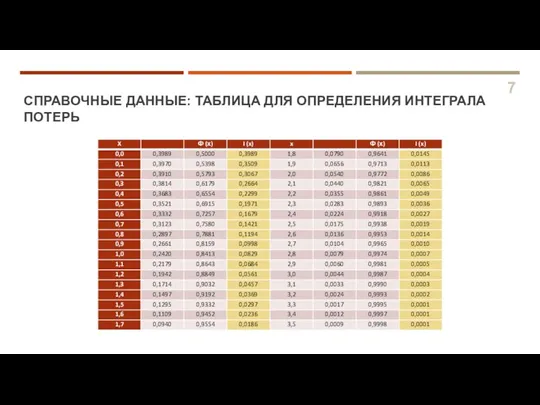
СПРАВОЧНЫЕ ДАННЫЕ: ТАБЛИЦА ДЛЯ ОПРЕДЕЛЕНИЯ ИНТЕГРАЛА ПОТЕРЬ
7

ПОРЯДОК РЕШЕНИЯ
8
Определить интеграл потерь для страхового запаса в 21 ед. Для этого рассчитать , затем по таблице найти интеграл потерь I()
Рассчитать суммарные затраты, связанные со страховым запасом (сумма затрат на хранение и потерь из-за дефицита):
=
Проверим, правильно ли был определен страховой запас. Для этого в табл. представим результаты расчетов для разных значений страхового запаса.
Расчет оптимальной величины страхового запаса

ПОРЯДОК РЕШЕНИЯ
9
Определим вероятность отсутствия дефицита при Qс =
F() =
Рассчитаем также «коэффициент удовлетворения спроса» или «уровень доступности запасов»:
=
Вывод: При условии минимума затрат страховой запас составит __., вероятность отсутствия дефицита будет равна __, а коэффициент удовлетворения спроса __.

ЗАДАНИЕ 4. ОПРЕДЕЛИТЬ ТЕКУЩИЙ И СТРАХОВОЙ ЗАПАС
10
ПОРЯДОК РЕШЕНИЯ
Исходные данные: потребность А=1000 ед/год; затраты на выполнение заказа Со=100 руб.; затраты на хранение единицы продукции cх=20 руб./ед.год; хp=2,0 (при Р=0,96); σD=2,54 ед/день; D=5 ед/день. Запас полоняется через фиксированные интервалы времени между заказами.
Решим задание численным методом, для этого заполним табл.
Расчет величины текущего запаса (с учетом страхового запаса)

ПОРЯДОК РЕШЕНИЯ
11
Вывод: Оптимальная величина текущего запаса находится в диапазоне 75-95 ед.
Уточним величину текущего запаса, воспользовавшись итерационной процедурой
Пусть Q0=95 ед., тогда
второе приближение при Q1=
Определим размер страхового запаса:
Суммарный запас составляет:
Сравним результаты с расчетом, соответствующим другому подходу: