Уравнением линии на плоскости

4.1. Уравнение прямой на плоскости
Уравнением линии на плоскости XOY
называется уравнение, которому удовлетворяют
координаты x и y каждой точки этой линии
и не удовлетворяют координаты любой точки,
не лежащей на этой линии.
В общем случае уравнение линии может быть записано в виде
или

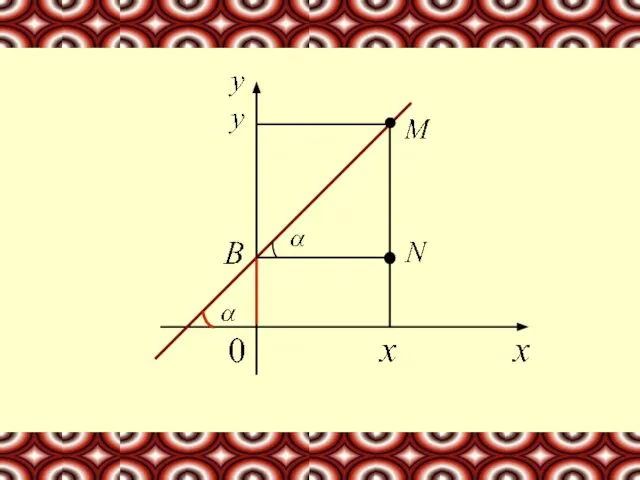
Пусть задана прямая, пересекающая ось у в точке В (0,в) и образующая с осью х угол α
Выберем на прямой произвольную точку М(х,у).
Способы задания
прямой на плоскости
1. Уравнение прямой с
угловым коэффициентом

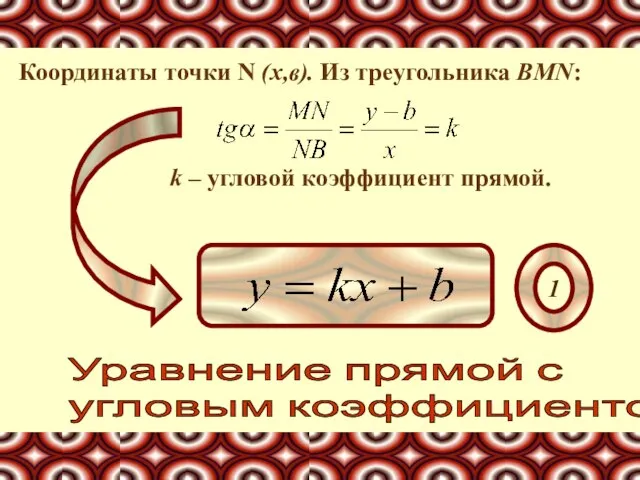
Координаты точки N (x,в). Из треугольника BMN:
k – угловой коэффициент прямой.
Уравнение прямой с
угловым коэффициентом
1

Рассмотрим частные случаи:
- уравнение прямой, проходящей через начало координат.
1
2
- уравнение прямой, параллельной оси х.

т.е. у вертикальной прямой нет углового коэффициента.
3
- не существует
Уравнение прямой, параллельной оси у, в этом случае имеет вид
где а – отрезок, отсекаемый прямой на оси х.

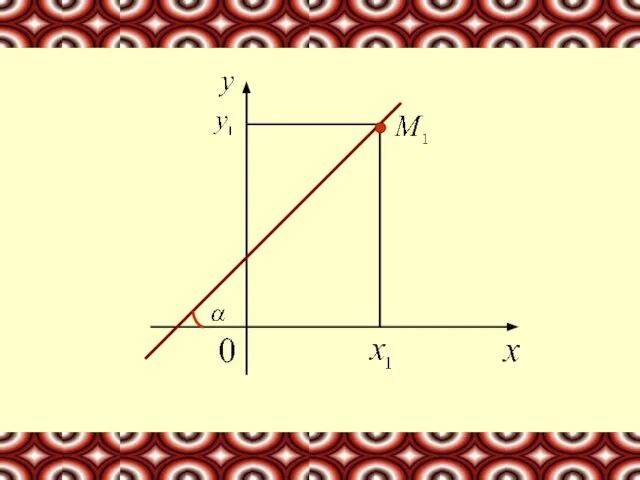
Пусть задана прямая, проходящая через заданную точку
2. Уравнение прямой, проходящей
через заданную точку в заданном направлении
и образующая с осью х угол α

Т.к. точка М1 лежит на прямой, ее координаты должны удовлетворять уравнению (1):
Вычитаем это уравнение из уравнения (1):
Уравнение прямой,
проходящей через данную
точку в данном направлении
2

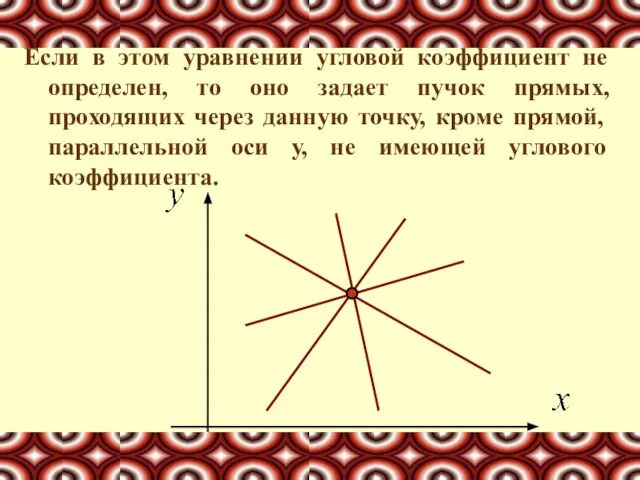
Если в этом уравнении угловой коэффициент не определен, то оно задает пучок прямых, проходящих через данную точку, кроме прямой, параллельной оси у, не имеющей углового коэффициента.

Пусть задана прямая, проходящая через две точки:
3. Уравнение прямой, проходящей
через две точки
Запишем уравнение пучка прямых, проходящих через точку М1:

Т.к. точка М2 лежит на данной прямой, подставим ее координаты в уравнение пучка прямых:
Подставляем k в уравнение пучка прямых. Тем самым мы выделяем из этого пучка прямую, проходящую через две данные точки:

или
Уравнение прямой,
проходящей через две точки
3

ПРИМЕР.
Составить уравнение прямой,
проходящей через точки А(-5,4) и
В(3,-2).

РЕШЕНИЕ.
Подставляем координаты точек в уравнение прямой, проходящей через две точки.

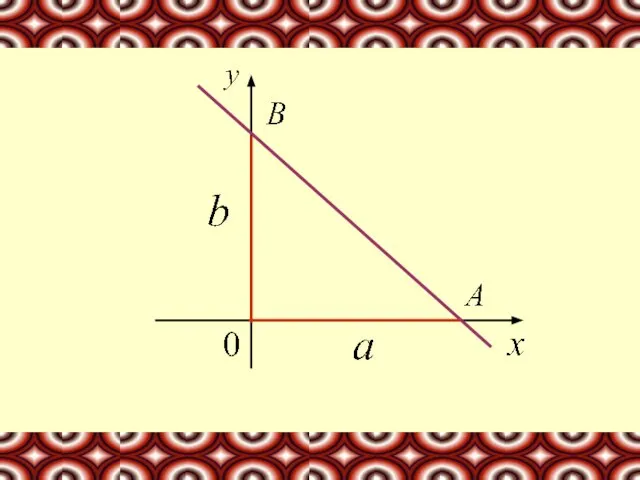
Пусть задана прямая, отсекающая на осях координат отрезки, равные а и в.
Это значит, что она проходит через точки
4. Уравнение прямой в отрезках
Найдем уравнение этой прямой.

Подставим координаты точек А и В в уравнение прямой, проходящей через две точки (3):
4
Уравнение прямой
в отрезках

ПРИМЕР.
Составить уравнение прямой,
проходящей через точку А(2,-1) если она
отсекает от положительной полуоси у
отрезок, вдвое больший, чем на
положительной полуоси х.

РЕШЕНИЕ.
По условию задачи,
Подставляем в уравнение (4):
Точка А(2,-1) лежит на этой прямой, следовательно ее координаты удовлетворяют этому уравнению:

Рассмотрим уравнение:
5. Общее уравнение прямой
Рассмотрим частные случаи этого уравнения и покажем, что при любых значениях коэффициентов А, В (не равных нулю одновременно) и С, это уравнение есть уравнение прямой на плоскости.
5

Тогда уравнение (5) можно представить в виде:
Тогда получаем уравнение (1):
Обозначим:
1

Тогда уравнение имеет вид:
Получаем уравнение:
- уравнение прямой, проходящей через начало координат.
2
3
- уравнение прямой, параллельной оси х.

Тогда уравнение имеет вид:
Получаем уравнение:
- уравнение оси х.
4
5
- уравнение прямой, параллельной оси у.