Содержание
- 2. Определять положение любой точки механической системы Научиться описывать движение механической системы с несколькими степенями свободы Цель
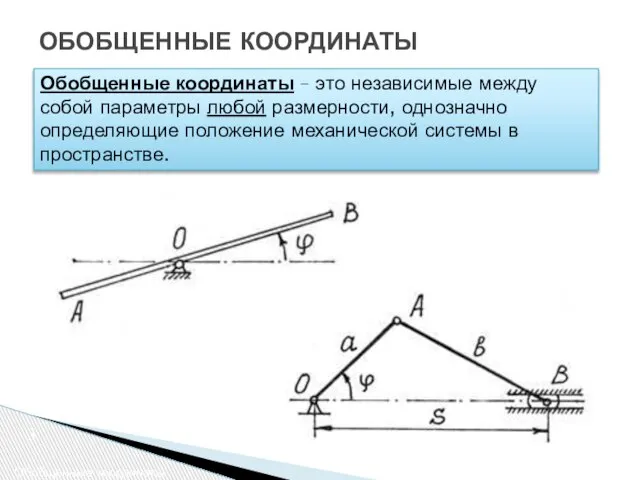
- 3. Обобщенные координаты Обобщенные координаты – это независимые между собой параметры любой размерности, однозначно определяющие положение механической
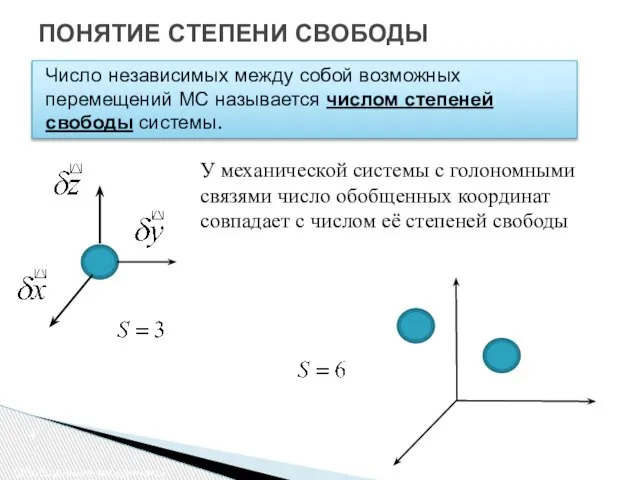
- 4. ПОНЯТИЕ СТЕПЕНИ СВОБОДЫ Число независимых между собой возможных перемещений МС называется числом степеней свободы системы. 4
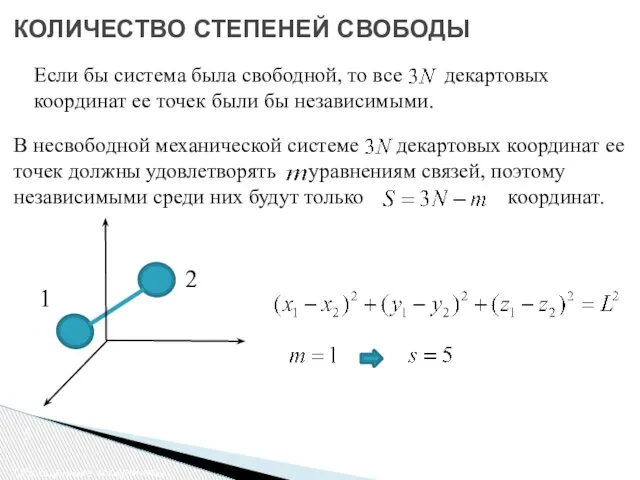
- 5. В несвободной механической системе декартовых координат ее точек должны удовлетворять уравнениям связей, поэтому независимыми среди них
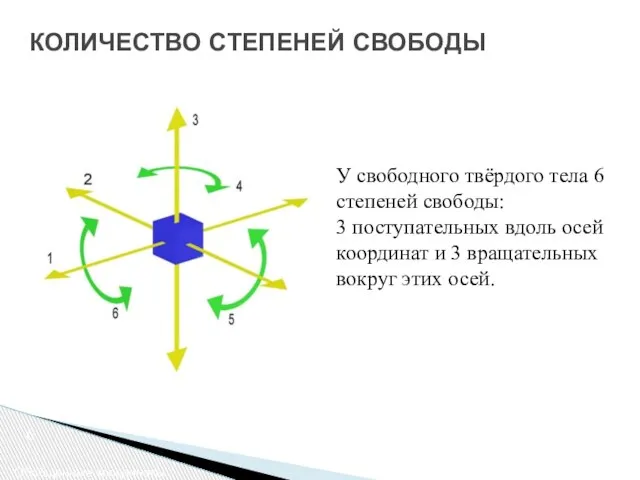
- 6. 6 КОЛИЧЕСТВО СТЕПЕНЕЙ СВОБОДЫ Обобщенные координаты У свободного твёрдого тела 6 степеней свободы: 3 поступательных вдоль
- 7. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТОЧЕК МС Тогда радиус-векторы всех точек системы можно определить как функцию обобщенных координат Обобщенные
- 8. ОБОБЩЁННЫЕ СКОРОСТИ Обобщенные скорости При движении системы её обобщённые координаты будут меняться со временем по закону
- 9. ОБОБЩЁННЫЕ СИЛЫ Обобщенные силы Рассмотрим МС, состоящую из n материальных точек, на которые действуют силы Пусть
- 10. ОБОБЩЁННЫЕ СИЛЫ Обобщенные силы Поскольку изменяется только координата , то вычисляется как частный дифференциал Тогда вычислим
- 11. ОБОБЩЁННЫЕ СИЛЫ Обобщенные силы - обобщённая сила, соответствующая координате
- 12. 12 Обобщённые силы – это величины, равные коэффициентам при приращениях обобщённых координат в выражении полной элементарной
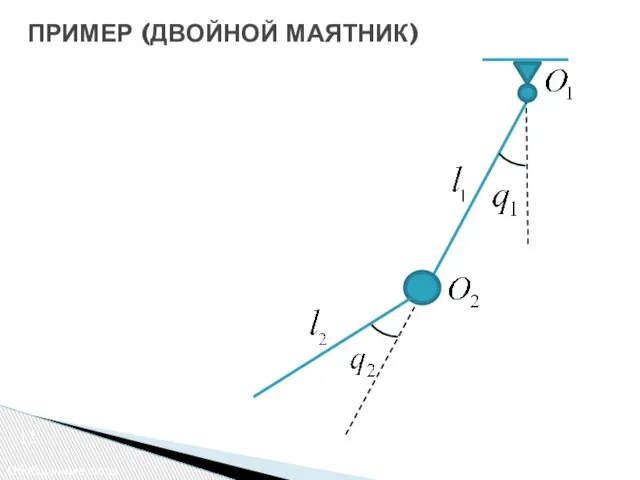
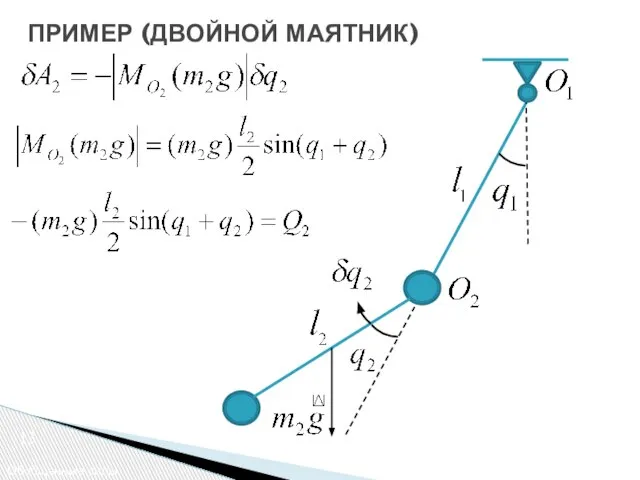
- 13. 13 Обобщенные силы ПРИМЕР (ДВОЙНОЙ МАЯТНИК)
- 14. 13 Обобщенные силы ПРИМЕР (ДВОЙНОЙ МАЯТНИК)
- 16. Скачать презентацию







 Шишкин Иван Иванович
Шишкин Иван Иванович Императоры Рима
Императоры Рима Chelovek_biosotsialnaya_suschnost
Chelovek_biosotsialnaya_suschnost Профилактика подросткового суицида
Профилактика подросткового суицида Международные отношения в конце XX - начале XXI в.в
Международные отношения в конце XX - начале XXI в.в Урок русского языка в 6 классе №1 Учитель Сухицкая В.Т.
Урок русского языка в 6 классе №1 Учитель Сухицкая В.Т. Профилактика инфекционных и неинфекционных заболеваний
Профилактика инфекционных и неинфекционных заболеваний Критерий выбора лучшего варианта конфигурации АРМ (тема 3)
Критерий выбора лучшего варианта конфигурации АРМ (тема 3) Презентация на тему экскурс в историю И новое прочтение пьесы «недоросль»
Презентация на тему экскурс в историю И новое прочтение пьесы «недоросль»  Доклад на тему:
Доклад на тему: Юные герои
Юные герои Let’s play (2 класс)
Let’s play (2 класс) Роль кластеров в развитии регионов
Роль кластеров в развитии регионов УЛУЧШЕНИЕ ПЕНСИОННОГО ОБЕСПЕЧЕНИЯ ЧЛЕНОВ ПРОФСОЮЗА ЧЕРЕЗ НЕГОСУДАРСТВЕННЫЙ ПЕНСИОННЫЙ ФОНД «ОБРАЗОВАНИЕ И НАУКА»
УЛУЧШЕНИЕ ПЕНСИОННОГО ОБЕСПЕЧЕНИЯ ЧЛЕНОВ ПРОФСОЮЗА ЧЕРЕЗ НЕГОСУДАРСТВЕННЫЙ ПЕНСИОННЫЙ ФОНД «ОБРАЗОВАНИЕ И НАУКА» Экскурсия в Тарусу Таруса — старинный русский город, административный центр Тарусского района Калужской обл. Расположен у впа
Экскурсия в Тарусу Таруса — старинный русский город, административный центр Тарусского района Калужской обл. Расположен у впа Гражданское общество
Гражданское общество Project template
Project template Хабибуллин Айрат 6Г
Хабибуллин Айрат 6Г Сущность и принципы корпоративного управления
Сущность и принципы корпоративного управления Почему мы спим ночью? (1 класс)
Почему мы спим ночью? (1 класс) HISTORY OF THEATRE
HISTORY OF THEATRE Музей в твоём классе
Музей в твоём классе Необычные музеии мира
Необычные музеии мира Презентация на тему Условные знаки Чтение топографического плана местности
Презентация на тему Условные знаки Чтение топографического плана местности  Школа Банкира 2.0
Школа Банкира 2.0 Презентация на тему Социальная психология, как наука
Презентация на тему Социальная психология, как наука  Итоговая аттестация выпускников 11-х классов
Итоговая аттестация выпускников 11-х классов Офисное помещение 181 кв.м на Невском, напротив метро «Маяковская»
Офисное помещение 181 кв.м на Невском, напротив метро «Маяковская»