Содержание
- 3. Дополнительно σ =1/2 и тогда При σ =1/2 схема называется схемой Крэнка–Николсона
- 4. 2. Устойчивость тогда по принципу максимума
- 5. Условие устойчивости по правой части Т.о. схема условно устойчива
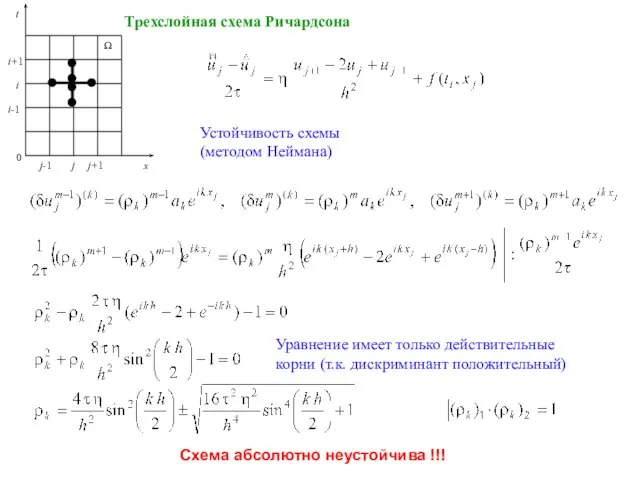
- 6. Трехслойная схема Ричардсона Устойчивость схемы (методом Неймана) Схема абсолютно неустойчива !!! Уравнение имеет только действительные корни
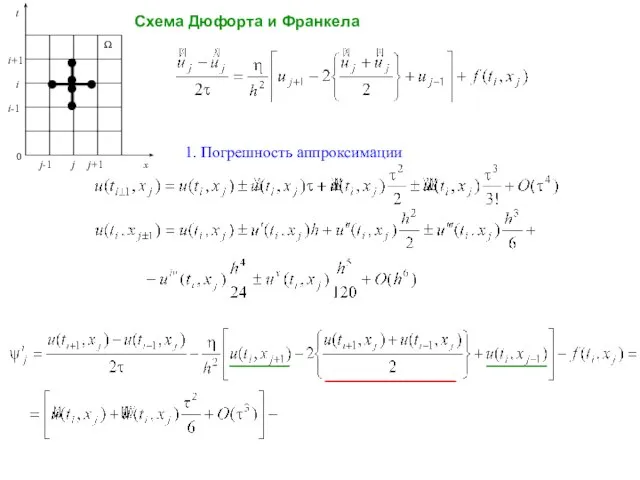
- 7. Схема Дюфорта и Франкела 1. Погрешность аппроксимации
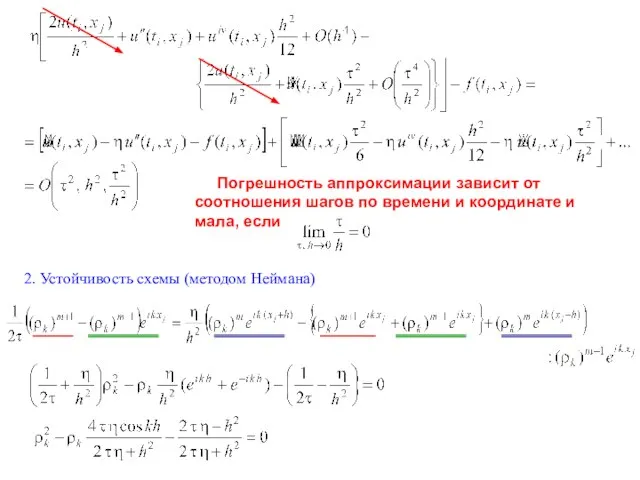
- 8. 2. Устойчивость схемы (методом Неймана) Погрешность аппроксимации зависит от соотношения шагов по времени и координате и
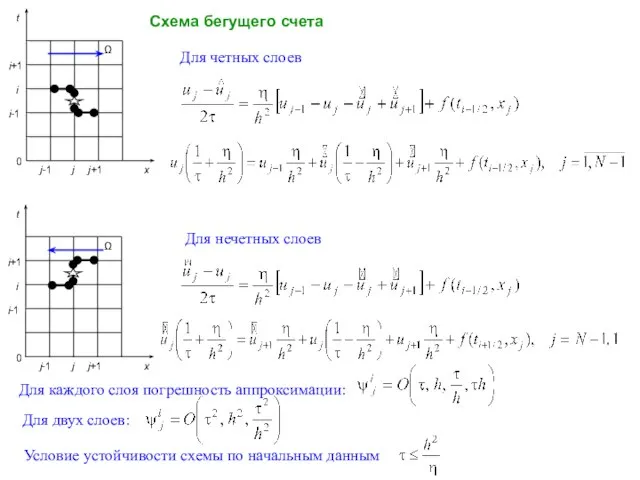
- 9. Схема бегущего счета Для четных слоев Для нечетных слоев Для каждого слоя погрешность аппроксимации: Для двух
- 10. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА начальные условия и граничные условия Схема «крест» 1. Погрешность аппроксимации
- 11. Полученная схема явная, трехслойная. Значения для нулевого временного слоя – из начальных условий на саму функцию.
- 12. 2. Устойчивость схемы по начальным данным (методом Неймана) По теореме Виета
- 13. Схема будет устойчива, если то есть корни будут комплексные (дискриминант отрицательный) Таким образом, схема условно устойчива
- 15. Скачать презентацию








 El uso del verbo SER
El uso del verbo SER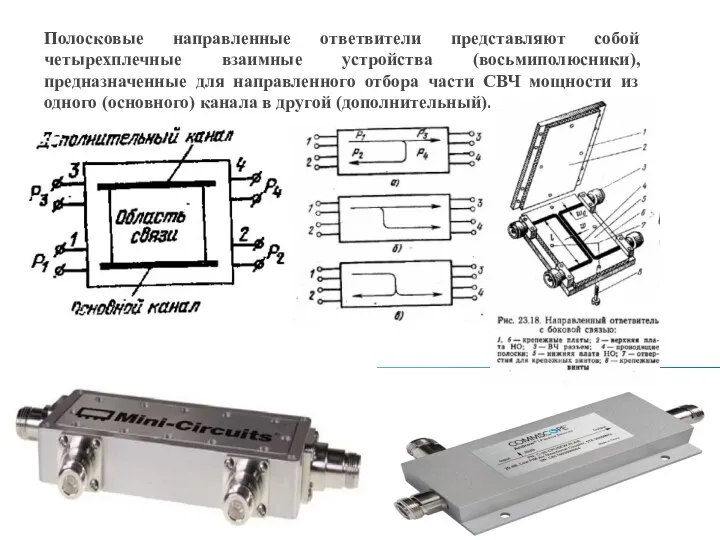 Направленные ответвители
Направленные ответвители Презентация на тему Презентация амурский тигр
Презентация на тему Презентация амурский тигр  Структура документа. Требования к оформлению документов. Лекция 4
Структура документа. Требования к оформлению документов. Лекция 4 Лексика и фразеология
Лексика и фразеология An Introduction to Software Architecture Case Studies
An Introduction to Software Architecture Case Studies Информационная система
Информационная система Западноевропейская архитектура, скульптура и живопись в X-XIV векахпрезентация Кудиновой Н.В. МОУСОШ№15 Тверь
Западноевропейская архитектура, скульптура и живопись в X-XIV векахпрезентация Кудиновой Н.В. МОУСОШ№15 Тверь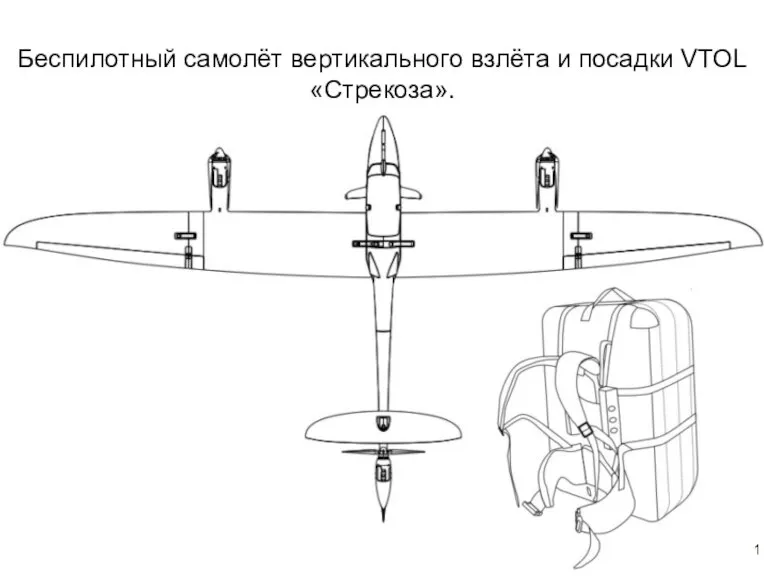 Дрон VTOL (1)
Дрон VTOL (1) Путешествие в Древний Восток
Путешествие в Древний Восток Презентация на тему Биотические факторы
Презентация на тему Биотические факторы  Банковская система и кредит. Ценные бумаги
Банковская система и кредит. Ценные бумаги СИСТЕМА ОЦЕНКИ ЗНАНИЙИ ПРИЁМЫ РАБОТЫПРИ БЕЗОТМЕТОЧНОМ ОБУЧЕНИИ В НАЧАЛЬНЫХ КЛАССАХ
СИСТЕМА ОЦЕНКИ ЗНАНИЙИ ПРИЁМЫ РАБОТЫПРИ БЕЗОТМЕТОЧНОМ ОБУЧЕНИИ В НАЧАЛЬНЫХ КЛАССАХ Школа грамотного потребителя
Школа грамотного потребителя Идентификация пользователей WiFi
Идентификация пользователей WiFi Walking Machine Technology
Walking Machine Technology Группа Компаний РОССЗОЛОТО
Группа Компаний РОССЗОЛОТО ПАО Новатэк
ПАО Новатэк Что_будет_с_рынком_недвижимости_часть_2
Что_будет_с_рынком_недвижимости_часть_2 Против коррупции
Против коррупции История создания сети интернет
История создания сети интернет С днем рождения доченька!
С днем рождения доченька! Режимы резания
Режимы резания Группа 2 Саморегулирование сети ОУ в условиях внедрения новых экономических механизмов в рамках КПМО.
Группа 2 Саморегулирование сети ОУ в условиях внедрения новых экономических механизмов в рамках КПМО. Насосы и электрооборудование насосов
Насосы и электрооборудование насосов Проект взаимодействия с нефтяными компаниями в области эффективной долгосрочной утилизации ПНГ
Проект взаимодействия с нефтяными компаниями в области эффективной долгосрочной утилизации ПНГ Тема Семинара
Тема Семинара 29 титульные листы отзывов
29 титульные листы отзывов