Уравнения Ричардсона и энергия связи куперовской пары В. В. Погосов, Институт теоретической и прикладной электродинамики РАН, Мос

Мотивация/Введение
Решение уравнений Ричардсона в разреженном пределе
Обобщение теории БКШ
Выводы
План

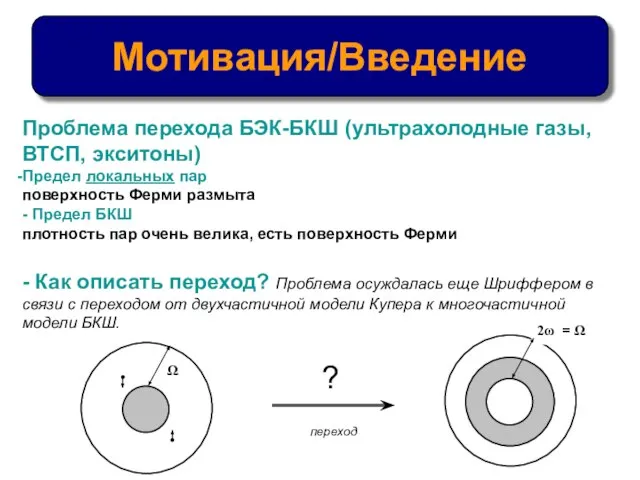
Мотивация/Введение
Проблема перехода БЭК-БКШ (ультрахолодные газы, ВТСП, экситоны)
Предел локальных пар
поверхность Ферми размыта
- Предел БКШ
плотность пар очень велика, есть поверхность Ферми
- Как описать переход? Проблема осуждалась еще Шриффером в связи с переходом от двухчастичной модели Купера к многочастичной модели БКШ.
?
переход

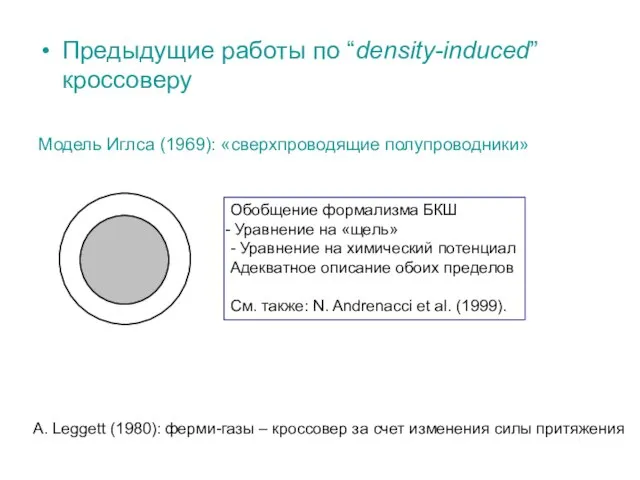
Предыдущие работы по “density-induced” кроссоверу
Модель Иглса (1969): «сверхпроводящие полупроводники»
Обобщение формализма БКШ
Уравнение на «щель»
- Уравнение на химический потенциал
Адекватное описание обоих пределов
См. также: N. Andrenacci et al. (1999).
A. Leggett (1980): ферми-газы – кроссовер за счет изменения силы притяжения

Задача Купера и теория БКШ: ключевые моменты
Задача Купера
Уравнение Шрёдингера:
Уравнение на собственные значения:
Энергия связи пары:
!

БКШ
Энергия сверхпроводящего состояния:
Сверхпроводящая щель:
Утверждение Шриффера: пары перекрыты так сильно, что
концепция изолированной пары не имеет смысла (“has a little meaning”)
- вводятся «виртуальные» пары с “энергией” = щели
- сконцентрированы вблизи поверхности Ферми
- отличаются от «сверхтекучих» пар из волновой функции БКШ
- их число гораздо меньше числа пар в слое
- вводятся не ab initio, а для понимания результата, «руками»
В настоящее время под куперовскими парами в БКШ обычно понимаются как раз виртуальные пары (см., например, Walecka-Fetter)
!

Мотивация:
- Установить возможную связь между «куперовскими парами» в обоих пределах
- Попытаться описать переход, выходя за рамки обобщенной теории БКШ
Альтернативное представление:

На примере двух пар
Подход Ричардсона
Мысленный эксперимент: начнем добавлять пары в слой, пока он не заполнится наполовину
R.W. Richardson (1963)
Волновая функция основного состояния:

используется тождество (расцепление):
Уравнения Ричардсона для двух пар

Уравнения Ричардсона для трех пар
- неявная зависимость от N !
- многочастичная классическая задача,
(имеется электростатическая аналогия)

Решение уравнений с помощью разложения
Разложение сумм в разреженном пределе
где
Вводим безразмерную переменную:

Приведенные уравнения Ричардсона для двух пар:
малый параметр
В первом приближении по :
(невзаимодействующие
пары)

Следующий порядок по :
Энергия основного состояния:
…переписываем:
добавление 1-ой пары
«выедание» энергии
связи пары (аналогично экситонам)

Три пары
В первом приближении:
Во втором приближении:
и т.д. для большего количества пар

Четное число пар (общий случай)
I. В первом приближении
Уравнения Ричардсона:
умножаем на ai и складываем
II. Во втором приближении (сумма уравнений Ричардсона):

Энергия основного состояния
Уменьшение энергии связи пары из-за принципа Паули
Полное совпадение с результатами БКШ при экстраполяции в «полузаполненную» конфигурацию!

Second order term in the expansion
still in N(N-1)
so that it vanishes in the large sample limit
M. Crouzeix & M. Combescot (unpublished)
Similar to Frenkel excitons
same one-to-one coupling …

Конфигурация с несимметричным расположением слоя с притяжением (произвольное число пар в слое)
Обобщение БКШ

Уравнение на щель

Вычисление энергии конденсации
Совпадение с результатами решения уравнений Ричардсона (N >> 1)

Подход можно обобщить и на «разреженный» предел
Добавляется уравнение на химпотенциал:
Выражения для энергии основного состояния и сохраняются, но меняется смысл
энергия возбужденного состояния:
слабая сингулярность

Спектр возбуждений из уравнений Ричардсона
- разрыв пары означает блокировку двух состояний («соловьевская блокировка»), что ведет к модификации энергии оставшихся пар
Начальное состояние: N пар
Конечное состояние: (N - 1) пара + 1 неспаренный электрон
Уравнения Ричардсона:

Разреженный предел:
Разница энергий:
конкуренция между кинетической энергией «дефекта» и изменением энергий оставшихся пар!
(!)
щель типа БКШ

На самом деле, должно выполняться неравенство:
Если не выполняется:
Итак,
в разреженном пределе выгодно поместить «дефект» как можно ниже. Энергия возбуждения контролируется энергией связи пары.
в плотном пределе выгодно поместить «дефект» повыше. Появляется щель типа БКШ. Поведение системы становится коллективным.
Щель типа БКШ – это многочастичный отклик системы.