Слайд 208/18/2023
Организация начала урока.
Здравствуйте ребята и дорогие гости! Сегодня мы

находимся на старте, правильные решения задач урока помогут нам продвинуться дальше. Мы с вами вспомним историю
нашего села, историю родной школы. Для этого путешествуем по стране «Показательной функции». Надеюсь, что вы активно включитесь в эту страну. Желаю успехов. Пусть будет сегодняшний девиз: «Больше узнать, больше усвоить».
Слайд 308/18/2023
Карточки
Три ученика получили задание на компьютере или на карточках.
Один ученик решает

на доске один пример домашнего задания
Слайд 408/18/2023
ТЕМА НАШЕГО УРОКА
« РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ»

Слайд 508/18/2023
ЦЕЛЬ УРОКА
Научится решать показательные уравнения.
Способствовать выработки навыка решения показательных

уравнений.
Проверка уровня усвоения темы.
Повторить и расширить сведения об уравнениях и способы их решения.
Слайд 608/18/2023
Итак, на старт. Первая остановка проверка домашнего задания.
Вопросы: 1. Дайте определение

показательной функции. Ответ. Функция, у = ах, а>0, а ≠ 1, называется показательной функцией с основанием а. Уравнение, содержащее переменную в показателе, называется показательной.
2. Перечислите основные свойства показательной функции.
3. Изобразите схематически графики функций:
а) у = 4x; в) у = (1/4)х; в) у = 6х; г) у = (1/6)х;
Какое уравнение служит простейшим примером показательного уравнения?
Ответ: ах = в, где а>0; а ≠ 1.
Какая область значений функции? Область значений показательной функции - множество положительных чисел. Поэтому в случае в меньше нуля или в равен нулю, показательное уравнение не имеет решение. Если больше нуля, то уравнение имеет единственный корень.
6. Как решается уравнение вида af(x) = ag(x)? Ответ: уравнение сводится к уравнению f(x) = g(x).
Слайд 708/18/2023
. Вторая остановка - Реши устно
Решите уравнения: 1. 3^х = 27

5. 6х – 3 = 36
2.( 1/7)х = 49 6. 3х = 273
3. 2х = 32 7. 9х = 273
4. 5х – 2 = 25 8. х∙ 4х = 0
Слайд 808/18/2023
Следующая остановка « Школа».
Чтобы перейти эту преграду надо решить четыре задачи,

с ответами составить четырехзначное число, связанное со школой.
1.Решить показательные уравнения:
а) 7^х + 1 + 4 ∙ 7^(х + 1) = 539
Слайд 908/18/2023
Решите уравнение.
б) Найти удвоенное произведение корня данного уравнения:
__
√3х

= 9
Слайд 1008/18/2023
Решите уравнение.
в) Найти утроенное произведение корня уравнения:
9^х – 8 ∙

3^х – 9 = 0
Слайд 1108/18/2023
Решите уравнение.
г) ___
√32х ∙ 5х = 2254,5

Слайд 1208/18/2023
Рассказ о школе.
Это число 1869 – организована наша школа

Слайд 1308/18/2023
Следующая остановка – «Историческая».
Чтобы войти в эту историю, решим следующие уравнения.
1.Найти

положительный корень. 9^х – 4 ∙ 3^х + 3 = 0
Слайд 1408/18/2023
Решите уравнение.
Найти квадрат корня данного уравнения.
9^х – 8 ∙ 3^(х+1) –

81 = 0
Слайд 1508/18/2023
Решите уравнение.
Найти корень 22^х – 4 ∙ 2^(х+1) + 16 = 0

Слайд 1608/18/2023
Решите уравнение.
Найти корень уравнения
3∙ 5^(2х – 1) - 2∙5 ^(х

– 1) = 0
Слайд 1708/18/2023
История села Раскильдино.
Вот четыре задачи решили, подытожим. Что же получилось теперь у

нас с ответами. Еще раз соберем ответы четырех задач.
Слайд 1808/18/2023
Остановка « Наши писатели нашего края».
1.Найти наибольший корень.
3 ∙

4^х – 5 ∙ 6^х + 2 ∙ 9^х = 0
Слайд 1908/18/2023
Решите уравнение.
2. Найти произведения числа 4,5 на корень уравнения.
7 ^(х

+ 1) - 5 ∙ 7^х = 98.
Слайд 2008/18/2023
Решите уравнение.
3. Найти сумму корней
___ ________
2√х + 1 =

16 ∙ √0, 255 – х/4
Слайд 2108/18/2023
А.С.Атремьев – 1924 г.

Слайд 2208/18/2023
1920 г.
1920 году образовано с.Раскильдино.

Слайд 2308/18/2023
Станция «Конечная»
Наше сегодняшнее путешествие подходит к концу. Мы прибываем на станцию «

Конечная», на которой подведем итоги. Мы познакомились некоторыми способами решения показательных уравнений, которые и будут на экзамене ЕГЭ.






















 Калевала - карело-финский поэтический эпос в обработке Элиаса Лённрота. Посёлок Калевала
Калевала - карело-финский поэтический эпос в обработке Элиаса Лённрота. Посёлок Калевала ОБРАЗОВАТЕЛЬНАЯ СИСТЕМА «ШКОЛА 2100»
ОБРАЗОВАТЕЛЬНАЯ СИСТЕМА «ШКОЛА 2100» Книги рекордов МТС!
Книги рекордов МТС! Комбинированный урок по географии и биологии. Разработали: Полянская Г.Н., Мелихова А.И.
Комбинированный урок по географии и биологии. Разработали: Полянская Г.Н., Мелихова А.И. Артросиндесмология
Артросиндесмология Перестраховочный рынок России
Перестраховочный рынок России Энергетика: вчера, сегодня, завтра
Энергетика: вчера, сегодня, завтра Анализ рекламных роликов
Анализ рекламных роликов ICDL международный образовательный стандарт по ИТ в Кыргызстане
ICDL международный образовательный стандарт по ИТ в Кыргызстане УПОТРЕБЛЕНИЕ ВРЕМЁН
УПОТРЕБЛЕНИЕ ВРЕМЁН Презентация на тему Второй рейх в Германии
Презентация на тему Второй рейх в Германии  ЗАВИСИМОСТЬ СКОРОСТИ ЗВУКА В ВОЗДУХЕ ОТ ЕГО СОСТОЯНИЯ
ЗАВИСИМОСТЬ СКОРОСТИ ЗВУКА В ВОЗДУХЕ ОТ ЕГО СОСТОЯНИЯ Ванны
Ванны Астероиды, метеоры, метеориты
Астероиды, метеоры, метеориты Васек Трубачев и другие
Васек Трубачев и другие Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений
Правила проведения аварийно-спасательных работ при обрушении зданий и сооружений Бизнес–план. Модуль 3. Маркетинг. ДекорАРТ
Бизнес–план. Модуль 3. Маркетинг. ДекорАРТ Элементы литературоведческого анализа стихотворения А.С. Пушкина «И.И. Пущину»
Элементы литературоведческого анализа стихотворения А.С. Пушкина «И.И. Пущину» Первые русские храмы
Первые русские храмы Память как высшая психологическая функция
Память как высшая психологическая функция Презентация на тему Current events
Презентация на тему Current events  Великобритания
Великобритания Живописцы и скульпторы
Живописцы и скульпторы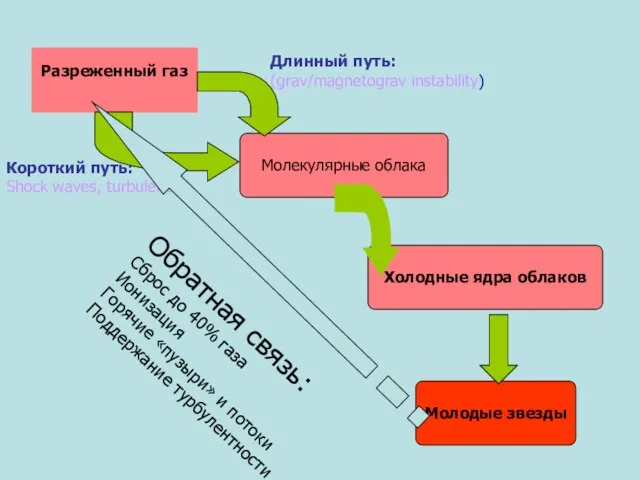 Разреженный газ Молекулярные облака Холодные ядра облаков
Разреженный газ Молекулярные облака Холодные ядра облаков Возникновение первой азбуки
Возникновение первой азбуки Право, его роль в жизни общества и государства
Право, его роль в жизни общества и государства “У каждого народа те правители, каких он заслуживает”. “У каждого народа те правители, каких он заслуживает”. историк Хилер Бэллок
“У каждого народа те правители, каких он заслуживает”. “У каждого народа те правители, каких он заслуживает”. историк Хилер Бэллок Вычисления с помощью калькулятора - презентация для начальной школы_
Вычисления с помощью калькулятора - презентация для начальной школы_