Содержание
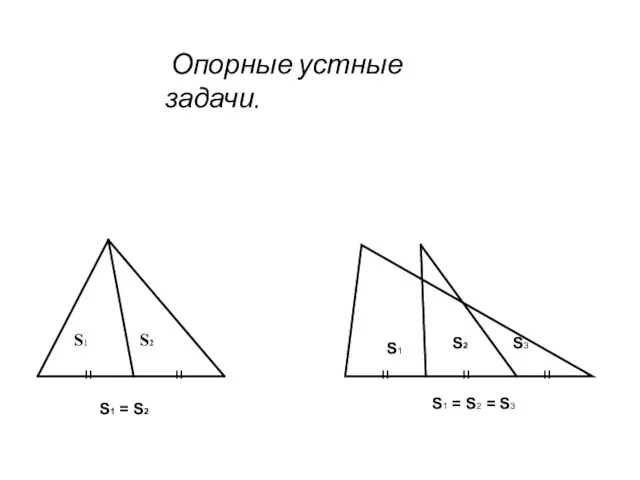
- 2. S1 S2 װ װ S1 = S2 װ װ װ S1 S2 S3 S1 = S2
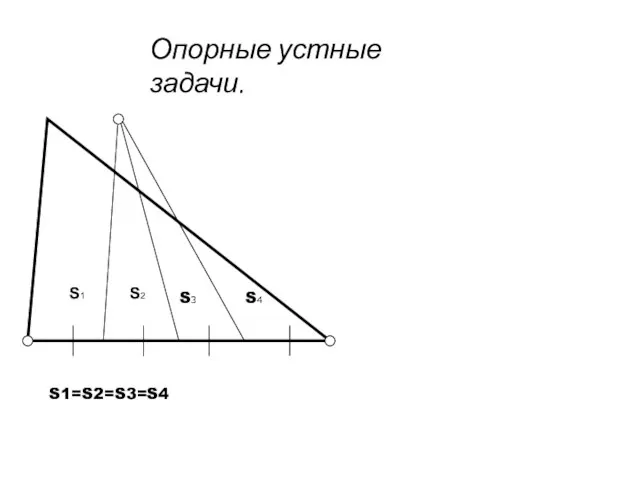
- 3. Опорные устные задачи. S3 S4 S1=S2=S3=S4 S1 S2
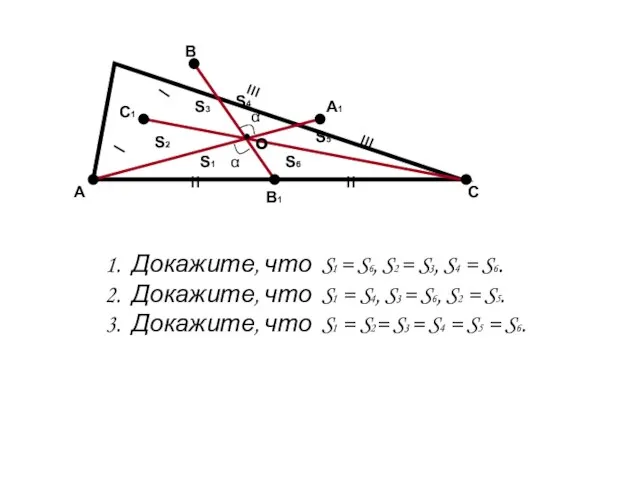
- 4. А С В В1 С1 А1 ≡ ≡ װ װ _ _ о α α S1
- 5. Решение геометрических задач методом дополнительного построения Главный руководитель : КОНЕВА ГАЛИНА МИХАЙЛОВНА Выполнили работу ученики 9
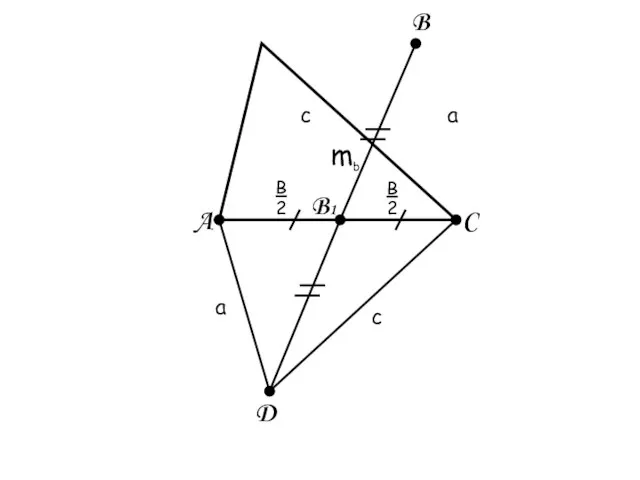
- 6. ЗАДАЧА №1 Найти медианы треугольника, если известны стороны a,b,c.
- 7. A B C B1 D mb B 2 B 2 c c a a
- 8. Решение: (2mb) +b =2(a +c ) 4mb =2a +2c -b mb = 2a +2c -b Аналогично
- 9. Рациональное решение геометрической задачи. Выполнили: Асеева Мария, Притупова Кристина, Капустина Оля
- 10. Найти площадь треугольника по трем известным медианам: 3, 4, 5. ЗАДАЧА №2
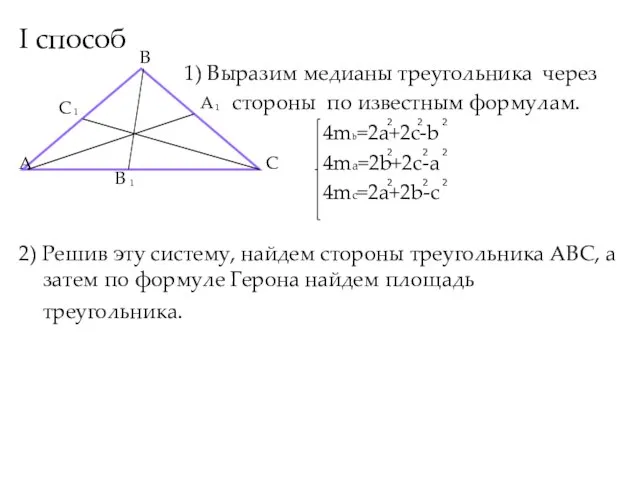
- 11. I способ 1) Выразим медианы треугольника через стороны по известным формулам. 4mb=2a+2c-b 4ma=2b+2c-a 4mc=2a+2b-c 2) Решив
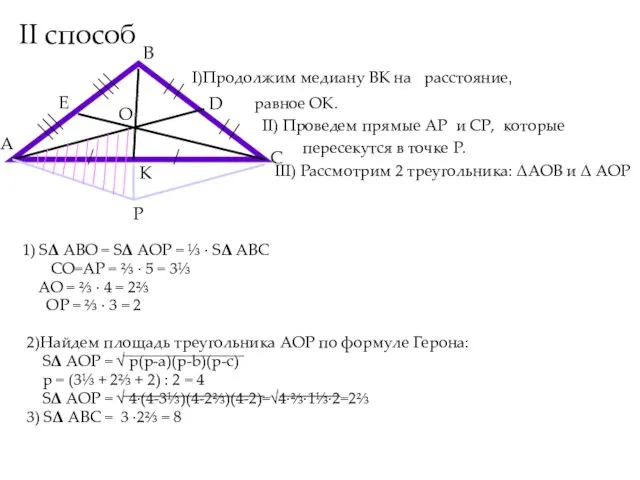
- 12. II способ I)Продолжим медиану ВК на расстояние, равное ОК. II) Проведем прямые АP и СP, которые
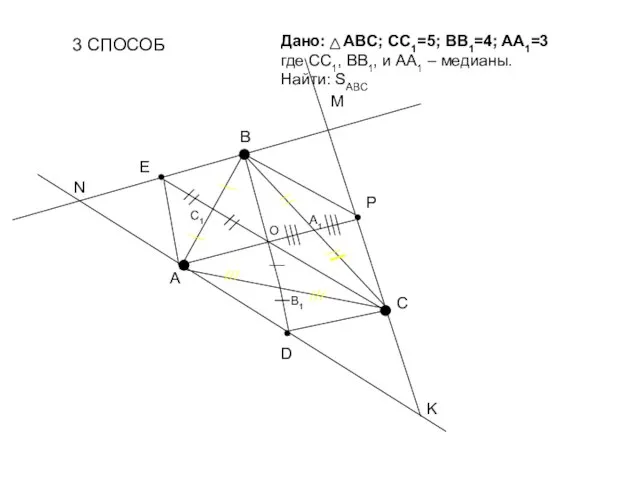
- 13. 3 СПОСОБ О Дано: ABC; CC1=5; BB1=4; AA1=3 где СС1, ВВ1, и АА1 – медианы. Найти:
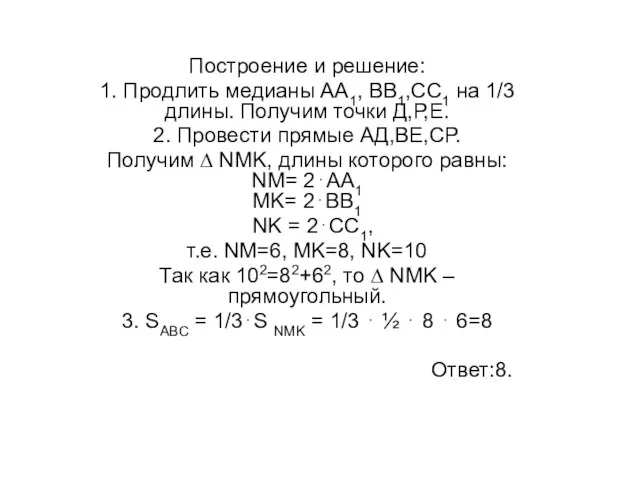
- 14. Построение и решение: 1. Продлить медианы АА1, ВВ1,СС1 на 1/3 длины. Получим точки Д,Р,Е. 2. Провести
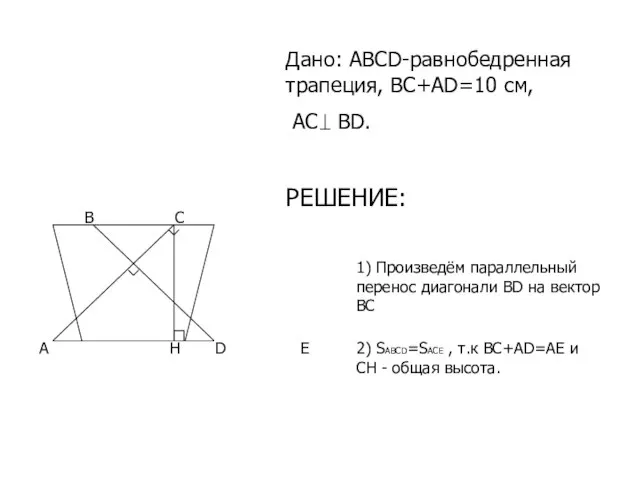
- 15. ЗАДАЧА №3 Диагонали равнобедренной трапеции взаимно перпендикулярны, а сумма её оснований равна 10 см. Найти площадь
- 16. D A B C E 1) Произведём параллельный перенос диагонали BD на вектор ВС 2) SABCD=SACE
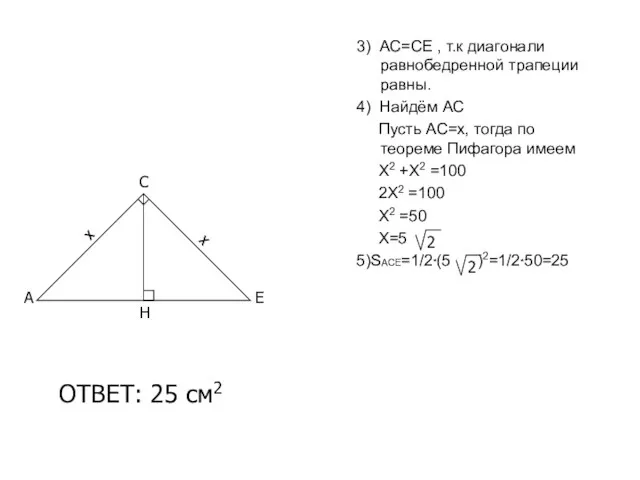
- 17. 3) АС=СЕ , т.к диагонали равнобедренной трапеции равны. 4) Найдём АС Пусть АС=х, тогда по теореме
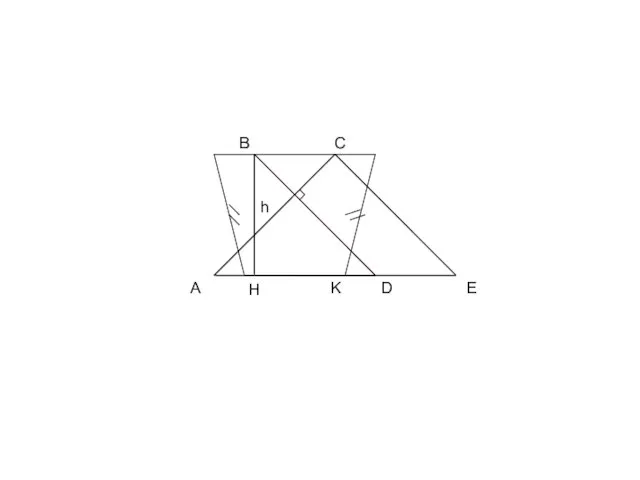
- 18. ЗАДАЧА №4 Найдите площадь равнобедренной трапеции, у которой высота равна h, а диагонали взаимно перпендикулярны.
- 19. А В С H D h E K
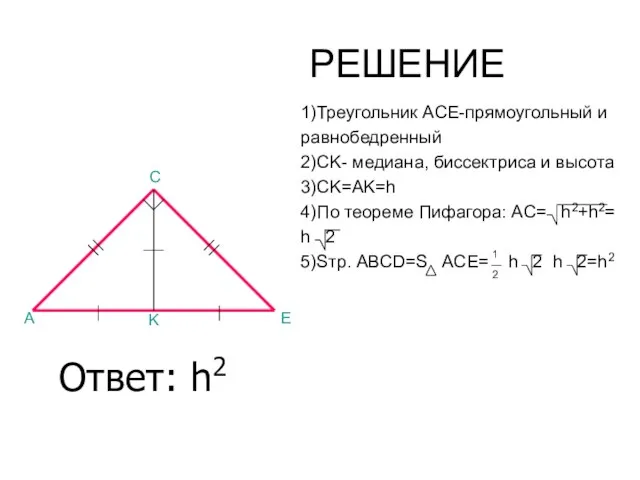
- 20. РЕШЕНИЕ 1)Треугольник ACE-прямоугольный и равнобедренный 2)CK- медиана, биссектриса и высота 3)CK=AK=h 4)По теореме Пифагора: AC= h2+h2=
- 21. Задача №5 Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найти
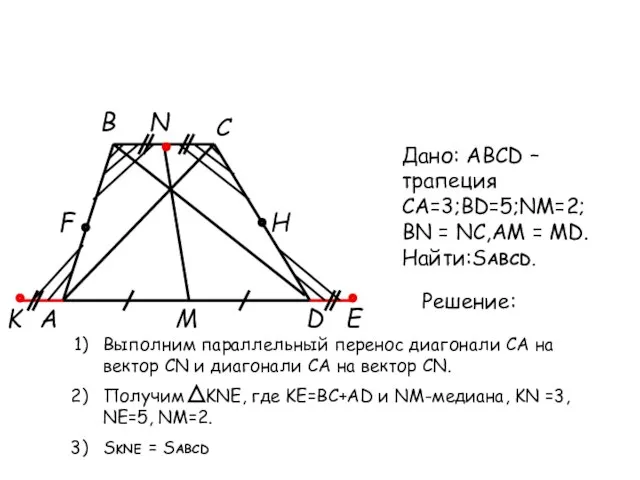
- 22. A B C D N M K E F H Дано: ABCD – трапеция CA=3;BD=5;NM=2;BN =
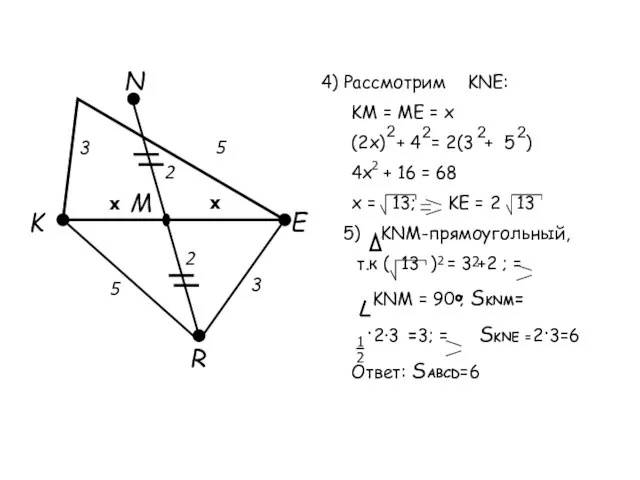
- 23. 4) Рассмотрим KNE: K N E R M x x 3 3 2 2 5 5
- 24. Задача №6 В трапеции ABCD AC перпендикулярна BD. АС=16, BD=12. Найти среднюю линию. ( Эта задача
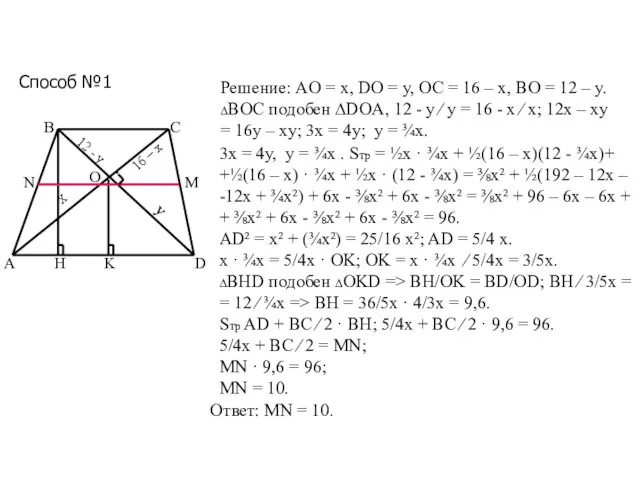
- 25. Способ №1 А В C D О K H Х y 12 - y 16 –
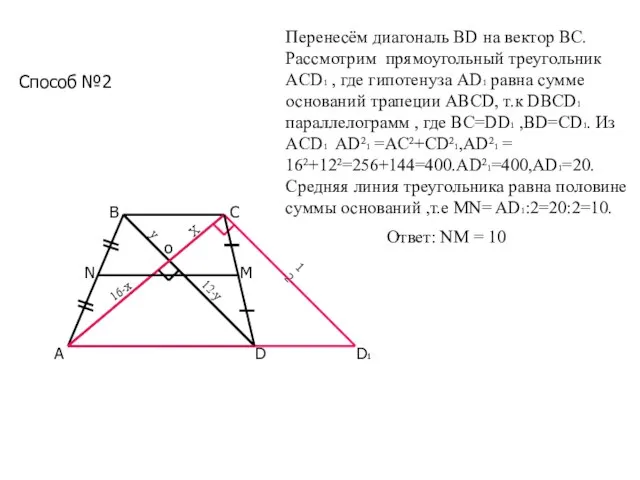
- 26. А В D D1 Перенесём диагональ BD на вектор ВС. Рассмотрим прямоугольный треугольник ACD1 , где
- 28. Скачать презентацию









 Презентация на тему Скелет
Презентация на тему Скелет  Презентация на тему Мультимедиа технологии
Презентация на тему Мультимедиа технологии  Презентация на тему картофель
Презентация на тему картофель Буква Ь в глаголах 2-го
Буква Ь в глаголах 2-го Изменим к лучшему жизнь детей с синдромом Дауна в России Благотворительный фонд «Даунсайд Ап»
Изменим к лучшему жизнь детей с синдромом Дауна в России Благотворительный фонд «Даунсайд Ап» Проектная площадка № 3
Проектная площадка № 3 Муниципальное образовательное учреждение Староянашевская основная общеобразовательная школа Яльчикского района Чувашской Респ
Муниципальное образовательное учреждение Староянашевская основная общеобразовательная школа Яльчикского района Чувашской Респ Городской пейзаж
Городской пейзаж Проблема наркомании
Проблема наркомании Презентация на тему Мамин Сибиряк
Презентация на тему Мамин Сибиряк Кажым заглянем в прошлое
Кажым заглянем в прошлое Греция
Греция С днём ракетных войск и артиллерии
С днём ракетных войск и артиллерии Лекция 6. Общественное и частное призрение второй половины XIX по 1917 г.
Лекция 6. Общественное и частное призрение второй половины XIX по 1917 г. Управление трудовыми ресурсами
Управление трудовыми ресурсами 20170209_yuzhnaya_amerika
20170209_yuzhnaya_amerika Светская этика
Светская этика Добро пожаловать в команду МИРАТОРГ
Добро пожаловать в команду МИРАТОРГ Презентация
Презентация Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Развитие продуктов и услугна статичных рынках
Развитие продуктов и услугна статичных рынках Реализация проектов энергосбережения в различных секторах экономики
Реализация проектов энергосбережения в различных секторах экономики Гештальтпсихология
Гештальтпсихология КРИЗИС и региональные СМИ
КРИЗИС и региональные СМИ ROBOT MOEЙ MEЧТЫ
ROBOT MOEЙ MEЧТЫ Презентация Отчет МБОУ СОШ 23 4 класс А
Презентация Отчет МБОУ СОШ 23 4 класс А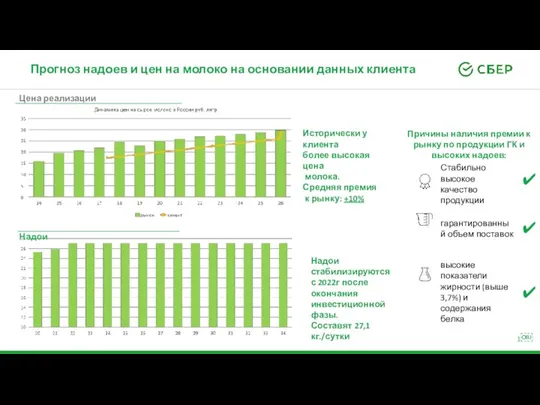 04 Прогнозы клиента
04 Прогнозы клиента Латинская Америка начала XX века
Латинская Америка начала XX века