Урок 14

Проверка выполнения домашнего задания

Самостоятельная работа (5 мин)

Что такое угловой коэффициент прямой?

Давайте на примере разберёмся, что это значит. Пусть у нас есть линейная функция ? = 2? + 1 и её график. На этом графике лежат, например, точки ? (0; 1), ? (1; 3) и ? (2; 5).

Отметим на клетчатой бумаге две точки, стоящие в углах клеточек, и проведём через них прямую.
Теперь проведём через каждую из этих точек вертикальную и горизонтальную прямые.
Получился треугольничек. Дальше мы будем рисовать только такие треугольнички, не проводя вертикальные и горизонтальные прямые. Эти треугольнички мы будем называть «ступеньками», потому что если нарисовать много таких треугольничков друг за другом, то их катеты образуют «лесенку».

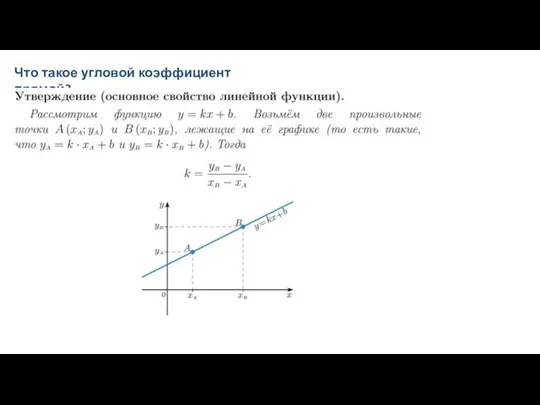
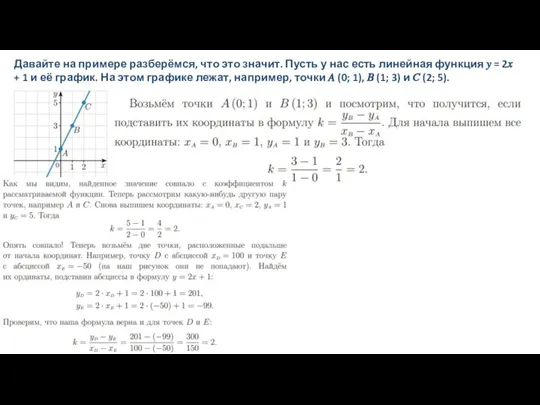
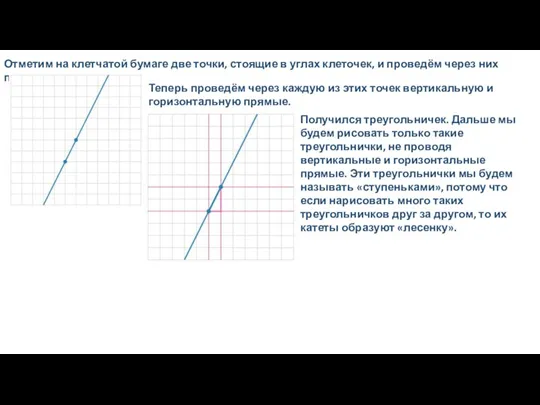
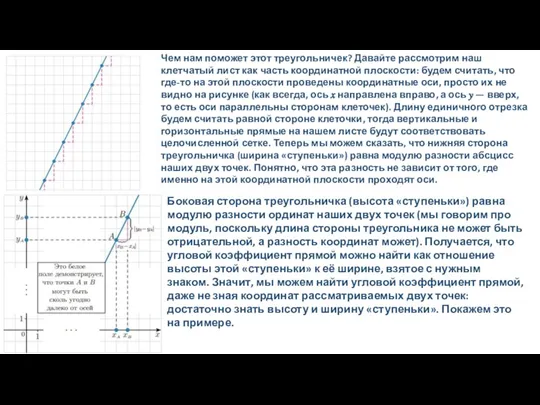
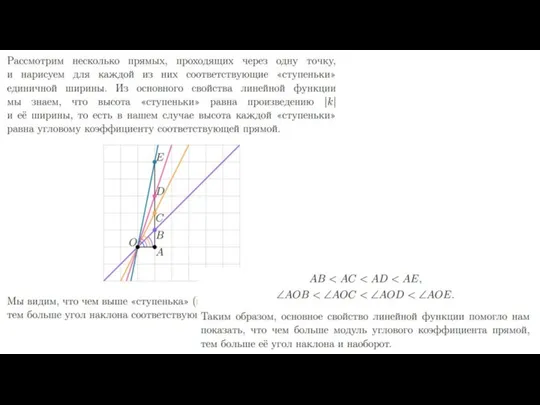
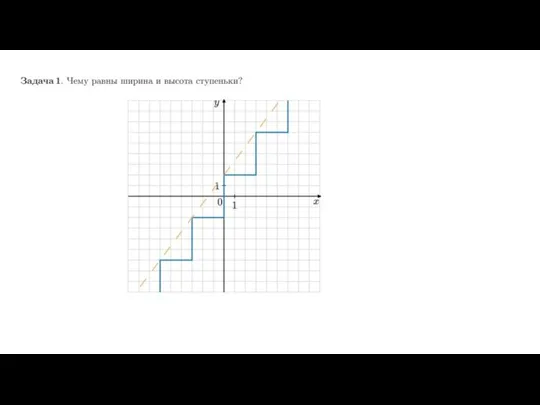
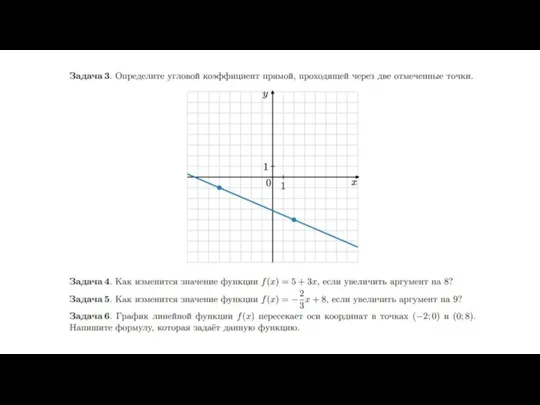
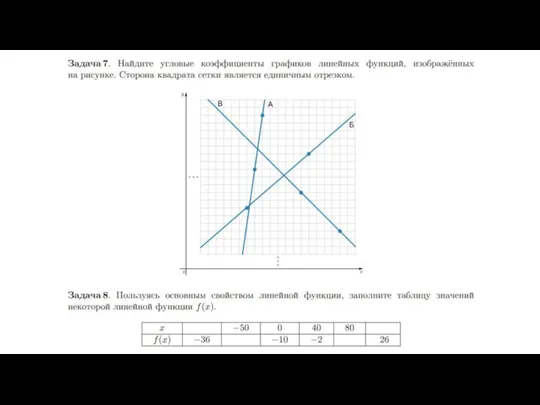
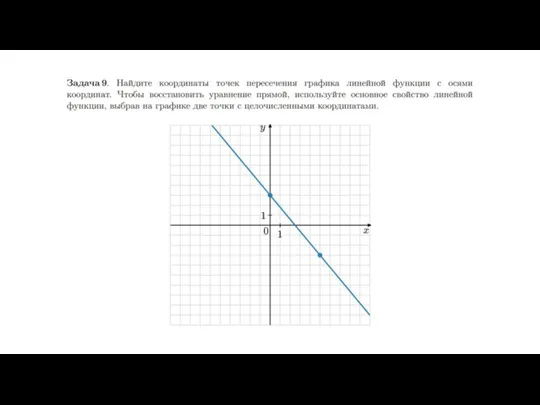
Чем нам поможет этот треугольничек? Давайте рассмотрим наш клетчатый лист как часть координатной плоскости: будем считать, что где-то на этой плоскости проведены координатные оси, просто их не видно на рисунке (как всегда, ось ? направлена вправо, а ось ? — вверх, то есть оси параллельны сторонам клеточек). Длину единичного отрезка будем считать равной стороне клеточки, тогда вертикальные и горизонтальные прямые на нашем листе будут соответствовать целочисленной сетке. Теперь мы можем сказать, что нижняя сторона треугольничка (ширина «ступеньки») равна модулю разности абсцисс наших двух точек. Понятно, что эта разность не зависит от того, где именно на этой координатной плоскости проходят оси.
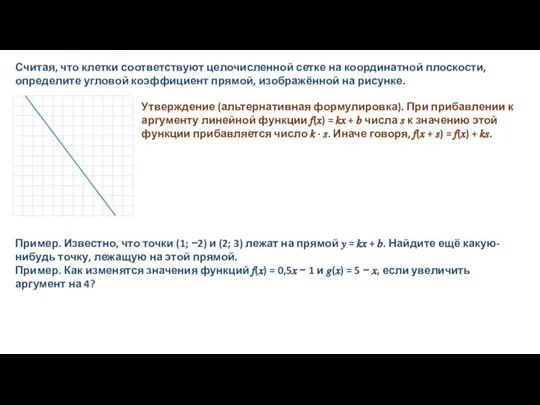
Боковая сторона треугольничка (высота «ступеньки») равна модулю разности ординат наших двух точек (мы говорим про модуль, поскольку длина стороны треугольника не может быть отрицательной, а разность координат может). Получается, что угловой коэффициент прямой можно найти как отношение высоты этой «ступеньки» к её ширине, взятое с нужным знаком. Значит, мы можем найти угловой коэффициент прямой, даже не зная координат рассматриваемых двух точек: достаточно знать высоту и ширину «ступеньки». Покажем это на примере.

Считая, что клетки соответствуют целочисленной сетке на координатной плоскости, определите угловой коэффициент прямой, изображённой на рисунке.
Утверждение (альтернативная формулировка). При прибавлении к аргументу линейной функции ?(?) = ?? + ? числа ? к значению этой функции прибавляется число ? · ?. Иначе говоря, ?(? + ?) = ?(?) + ??.
Пример. Известно, что точки (1; −2) и (2; 3) лежат на прямой ? = ?? + ?. Найдите ещё какую-нибудь точку, лежащую на этой прямой.
Пример. Как изменятся значения функций ?(?) = 0,5? − 1 и ?(?) = 5 − ?, если увеличить аргумент на 4?

Пример. Определите линейную функцию, график которой пересекает ось ? в точке с координатами (1; 0), а ось ? в точке с координатами (0; 2).

Домашнее задание