Содержание
- 2. Заголовок слайда Функция вида у = хr (где r - любое действительное число (в том числе
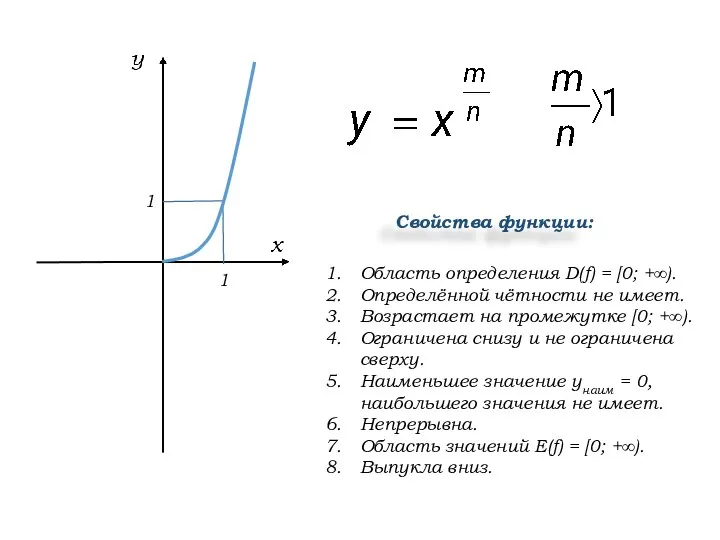
- 3. Область определения D(f) = [0; +∞). Определённой чётности не имеет. Возрастает на промежутке [0; +∞). Ограничена
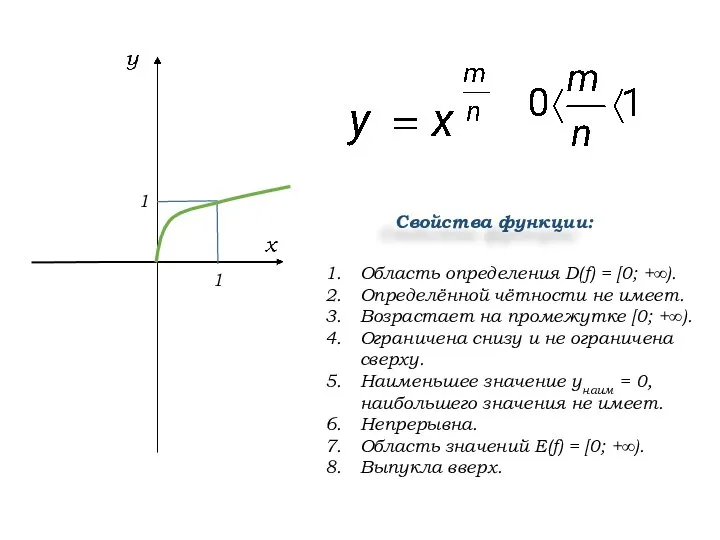
- 4. Область определения D(f) = [0; +∞). Определённой чётности не имеет. Возрастает на промежутке [0; +∞). Ограничена
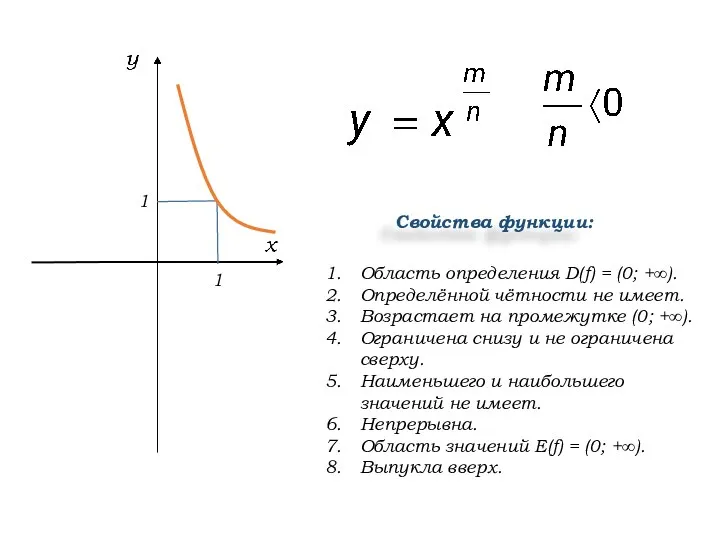
- 5. Область определения D(f) = (0; +∞). Определённой чётности не имеет. Возрастает на промежутке (0; +∞). Ограничена
- 6. Теорема. Если х>0 и r – любое рациональное число, то производная степенной функции y = xr
- 7. Пример 1. Найдём производную функции: При этом было использовано правило дифференцирования
- 8. Решение упражнений № 9.27 вг № 9.28 вг № 9.29 б № 9.14 вг
- 10. Скачать презентацию




 Мир геометрических фигур
Мир геометрических фигур Презентация на тему Организация и содержание физминутки на уроке
Презентация на тему Организация и содержание физминутки на уроке Мы за Новый мир! Движение за Новый Коммунизм
Мы за Новый мир! Движение за Новый Коммунизм Как выполнить выгрузкуотчетности в электронном виде из программ системы 1С:Предприятие
Как выполнить выгрузкуотчетности в электронном виде из программ системы 1С:Предприятие Неиспользуемые здания в коммунальной собственности Мостовского района, планируемые к продаже в 2012 году
Неиспользуемые здания в коммунальной собственности Мостовского района, планируемые к продаже в 2012 году СПП нерасчлененной структуры
СПП нерасчлененной структуры Курсовая работа
Курсовая работа Транспортное средство. Характеристика непрофильного актива
Транспортное средство. Характеристика непрофильного актива «Определение характерных черт портрета успешного предпринимателя »Проект Подготовили: Любченко Алёна и Няргинен ВикторияРуков
«Определение характерных черт портрета успешного предпринимателя »Проект Подготовили: Любченко Алёна и Няргинен ВикторияРуков И.И. Шишкин
И.И. Шишкин Круг обучения. Готовим профессионалов.
Круг обучения. Готовим профессионалов. Конституция Тыва
Конституция Тыва «Дело-КС» Автоматизация делопроизводства
«Дело-КС» Автоматизация делопроизводства Охрана материнства и детства в свете приоритетных правительственных программ Директор Департамента медико-социальных проблем с
Охрана материнства и детства в свете приоритетных правительственных программ Директор Департамента медико-социальных проблем с Тема проекта:«Здоровьесберегающие компоненты математического образования младшего школьника в свете стандарта второго поколен
Тема проекта:«Здоровьесберегающие компоненты математического образования младшего школьника в свете стандарта второго поколен Тургенев и Виардо
Тургенев и Виардо Менеджер по компенсациям и льготам. Профпереподготовка
Менеджер по компенсациям и льготам. Профпереподготовка 7 период развития соц.работы
7 период развития соц.работы Рынок труда: состав, состояние и перспективы развития.
Рынок труда: состав, состояние и перспективы развития. Игровые технологии в младшем школьном возрасте
Игровые технологии в младшем школьном возрасте Открытки с 9 мая
Открытки с 9 мая О введении комплексного курса
О введении комплексного курса Презентация на тему Народы России
Презентация на тему Народы России  Изменчивость. Мутации
Изменчивость. Мутации Презентация на тему Мастерство педагога
Презентация на тему Мастерство педагога Сирень 1945 года
Сирень 1945 года Методы составления и анализа семантического ядра
Методы составления и анализа семантического ядра Презентация на тему Одиночество
Презентация на тему Одиночество