Урок математики. 11 класс. 6 октября 2010 г.Преподаватель ГОУ № 671 Манасевич Н.А.РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

ЦЕЛЬ:
Обобщение знаний по решению тригонометрических уравнений.
Выделение основных проблем при решении этих уравнений:
Потеря корней.
Посторонние корни.
Отбор корней.

ПЛАН УРОКА.
Вводная часть, повторение теоретического материала. (Фронтальная работа)
Решение тригонометрических уравнений.(Групповая работа)
Проблемы, возникающие при решении тригонометрических уравнений.

Основные методы решения
тригонометрических уравнений
Разложение на множители.
Введение новой переменной.
Функционально – графический метод.

Некоторые типы тригонометрических уравнений
Уравнения, сводящиеся к квадратным, относительно
cosх = t, sinх = t.
A sin2 x + B cosx + C = 0
A cos2 x + В sinx + C = 0
Решаются методом введения новой переменной.
2.Однородные уравнения первой и второй степени.
I ст. A sinx + B cosx = 0 : cosx
A tg x + B = 0
II ст. A sin2 x + B sinx cosx + A cos2 x = 0 : cos2x
A tg2 x + B tgx + C = 0
Решаются методом разложения на множители и методом введения новой переменной.
3. Уравнение вида:
А sinx + B cosx = C. А, В, С ≠ 0
Применимы все методы.

4. Понижение степени.
А cos2x + В = C.
A cos2x + B = C.
Решаются методом разложения на множители.
A sin2x + B = C.
A sin2x + B = C.
Сводятся к однородным уравнениям С = С( ).
Сводятся к уравнению А sin2x + B cos2x = C.
5. Уравнение вида:
A(sinx + cosx) + B sin2x + C = 0.
Сводятся к квадратным относительно t = sinx + cosx.

Формулы
Универсальная подстановка.
х ≠ π + 2πn; Проверка обязательна!
Понижение степени.
= (1 + cos2x ) : 2
= (1 – cos2x) : 2
Метод вспомогательного аргумента.

Правила
Увидел квадрат – понижай степень.
Увидел произведение – делай сумму.
Увидел сумму – делай произведение.

1.Потеря корней:
делим на g(х).
опасные формулы (универсальная подстановка).
Этими операциями мы сужаем область определения.
2. Лишние корни:
возводим в четную степень.
умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.
Потеря корней, лишние корни.

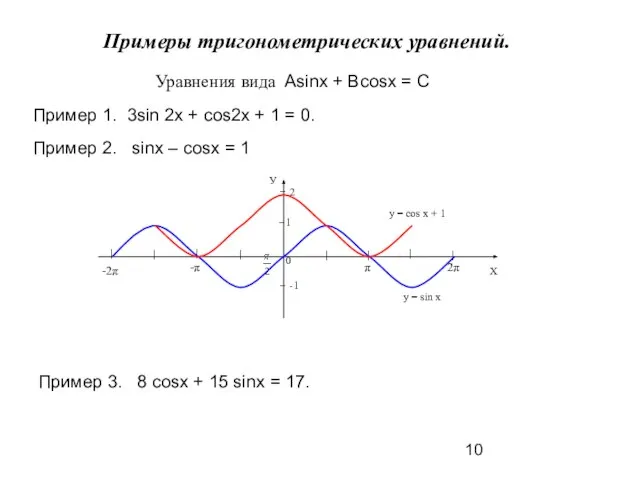
Примеры тригонометрических уравнений.
Пример 2. sinx – cosx = 1
Пример 3. 8 cosx + 15 sinx = 17.
Пример 1. 3sin 2x + cos2x + 1 = 0.
Уравнения вида Asinx + Bcosx = C

Проблемы, возникающие при решении тригонометрических уравнений
1.Потеря корней.
Делим на g(х).
Применяем опасные формулы.
Найдите ошибку.
2. Посторонние корни.
Освобождаемся от знаменателя.
Возводим в четную степень.

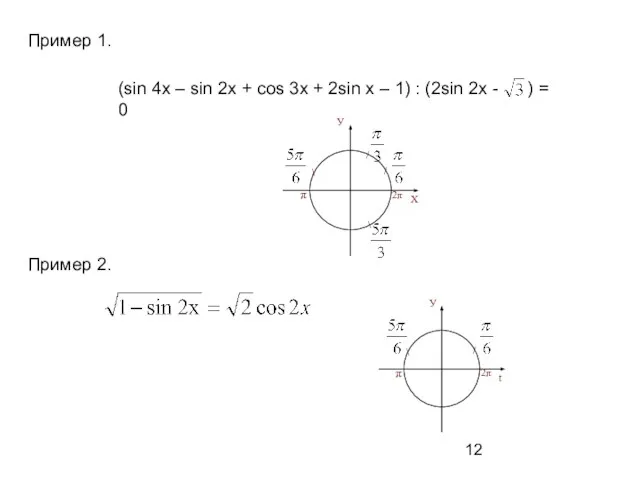
Пример 1.
Пример 2.