Содержание
- 2. Образовательные Закрепить и систематизировать знания учащихся по теме «Свойства арифметического квадратного корня» Сформировать умение применять их
- 3. Вопрос: Что называется арифметическим квадратным корнем ? Ответьте на вопрос
- 4. Вычислите: 1) √81 6) √36·√16 11) √ 0 2) √0,04 7) 3√9- 16 12) √-225 3)
- 5. 1) √16=4 2) √25=-5 3) √8=3 Вычислите: 4) √9=-3 5) √9=3 6) √64=|-8| Верны ли данные
- 6. Какие свойства арифметического квадратного корня вы знаете? Вопрос
- 7. Корень из произведения неотрицательных множителей равен произведению корней из этих множителей: √ а·в=√ а ·√ в,
- 8. Поменяв в тождествах √ а∙в = √ а ∙ √ в , где а≥0, в ≥0
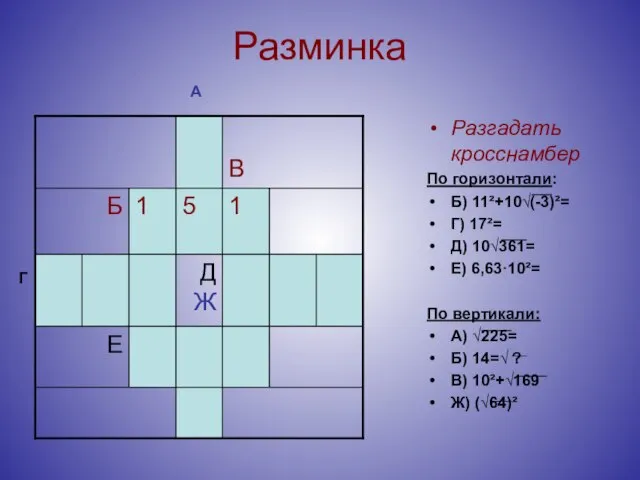
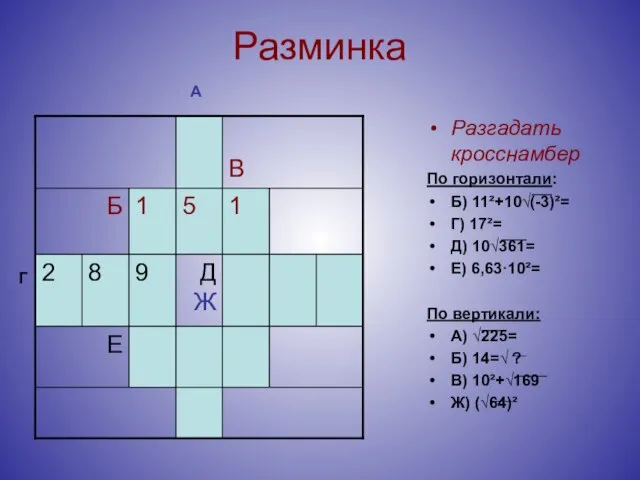
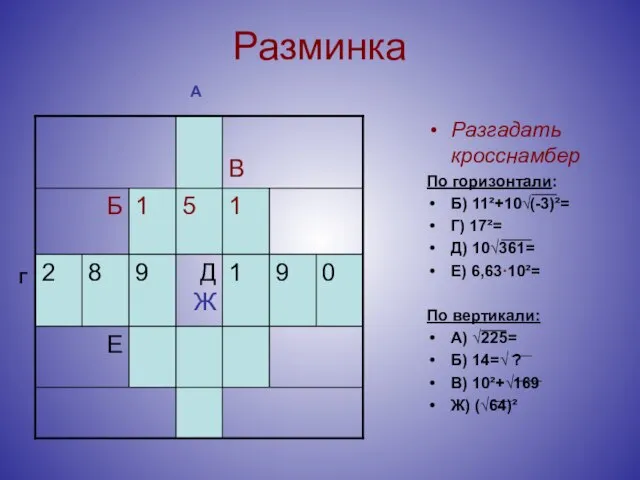
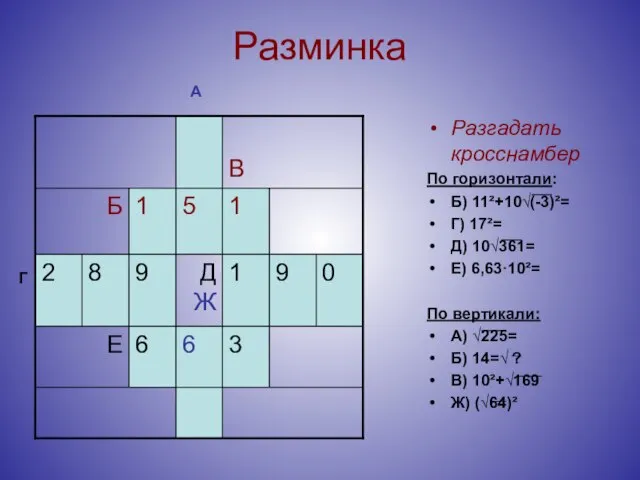
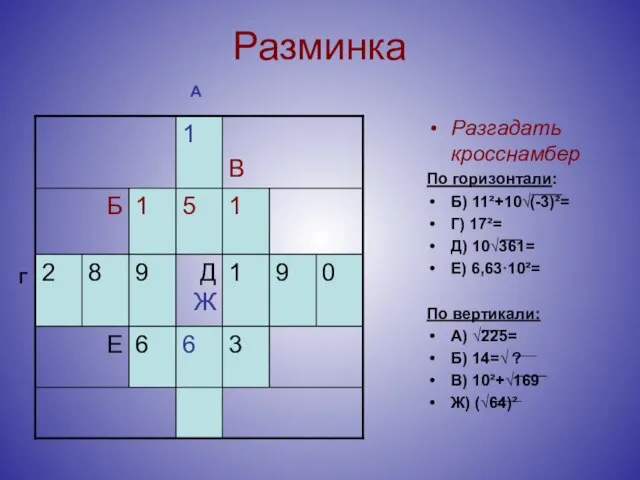
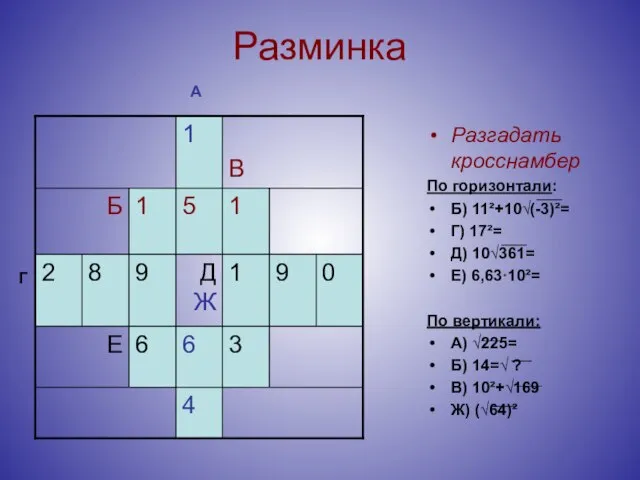
- 9. Разминка Разгадать кросснамбер По горизонтали: Б) 11²+10√(-3)²= Г) 17²= Д) 10√361= Е) 6,63·10²= По вертикали: А)
- 10. Разминка Разгадать кросснамбер По горизонтали: Б) 11²+10√(-3)²= Г) 17²= Д) 10√361= Е) 6,63·10²= По вертикали: А)
- 11. Разминка Разгадать кросснамбер По горизонтали: Б) 11²+10√(-3)²= Г) 17²= Д) 10√361= Е) 6,63·10²= По вертикали: А)
- 12. Разминка Разгадать кросснамбер По горизонтали: Б) 11²+10√(-3)²= Г) 17²= Д) 10√361= Е) 6,63·10²= По вертикали: А)
- 13. Разминка Разгадать кросснамбер По горизонтали: Б) 11²+10√(-3)²= Г) 17²= Д) 10√361= Е) 6,63·10²= По вертикали: А)
- 14. Разминка Разгадать кросснамбер По горизонтали: Б) 11²+10√(-3)²= Г) 17²= Д) 10√361= Е) 6,63·10²= По вертикали: А)
- 15. Разминка Разгадать кросснамбер По горизонтали: Б) 11²+10√(-3)²= Г) 17²= Д) 10√361= Е) 6,63·10²= По вертикали: А)
- 16. Работа по учебнику Решить: № 361(а,в), 372(в,г), 358(в,д),373(а,б)
- 17. Физкультминутка Вы на славу потрудились, И немного утомились, Дружно стать нам всем пора: Начинается игра!
- 18. Теорема. При любом значении х верно равенство √ х² =|х| Пример: √ (1,7)²=|1,7|= 1,7 √ (-19)²=|-19|=19
- 19. Упростите выражение Тест (контроль)
- 20. Интеллектуальная разминка Знание – самое превосходное из владений. Все стремятся к нему, само оно не приходит
- 21. Самопроверка
- 22. 1 вариант 2 вариант а) 2/3 а) 5/7 б) 3/4 б) 2/5 в) 8/9 в) 3/10
- 23. Работа по тестам Домашнее задание
- 24. К математике способность проявляй, Не ленись, а ежедневно развивай. Умножай, дели, трудись, соображай, С математикой дружить
- 26. Скачать презентацию

















 Конфликт как форма коммуникации
Конфликт как форма коммуникации Střední odborná škola podnikatelská PROFIT, s.r.o
Střední odborná škola podnikatelská PROFIT, s.r.o Гибкость и ее развитие
Гибкость и ее развитие Sap Ustavınıń tiykarǵı qaǵıydaları. Áskerdiń sapqa turıwdan aldıngı hám saptagı wazıypaları
Sap Ustavınıń tiykarǵı qaǵıydaları. Áskerdiń sapqa turıwdan aldıngı hám saptagı wazıypaları Инвестиционная деятельность и жилищное строительство
Инвестиционная деятельность и жилищное строительство Цікаві факти про Азовське море
Цікаві факти про Азовське море Античный скептицизм
Античный скептицизм Презентация
Презентация Удмуртский этнотуристический центр эштэрек
Удмуртский этнотуристический центр эштэрек Организация и проведение государственной итоговой аттестации по образовательным программам основного образования в 2018 году
Организация и проведение государственной итоговой аттестации по образовательным программам основного образования в 2018 году Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут
Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут Мулькиет ялгъамаларнынъ имлясы
Мулькиет ялгъамаларнынъ имлясы Общая характеристика институтов права: право собственности и обязательное право
Общая характеристика институтов права: право собственности и обязательное право 4
4 What colour is it? (Цвета, какой это цвет?)
What colour is it? (Цвета, какой это цвет?) Иллюстрационный материал к выпускной квалификационной работе: Совершенствование управления оборотными средствами
Иллюстрационный материал к выпускной квалификационной работе: Совершенствование управления оборотными средствами История многовековой дружбы народов России и Болгарии
История многовековой дружбы народов России и Болгарии Парный натюрморт Чайный (часть 1)
Парный натюрморт Чайный (часть 1) Лечение болей при диабетической полиневропатии с помощью аппарата HiToP®gbo Medizintechnik AG
Лечение болей при диабетической полиневропатии с помощью аппарата HiToP®gbo Medizintechnik AG Тема: "Адаптация ребенка к обучению в школе"
Тема: "Адаптация ребенка к обучению в школе" Моя малая Родина
Моя малая Родина Ravnomernoe_dvizhenie_po_okruzhnosti
Ravnomernoe_dvizhenie_po_okruzhnosti 经理对我印象不错
经理对我印象不错 Характеристика планет Солнечной Системы и НЕКОТОРЫХ известных звёзд
Характеристика планет Солнечной Системы и НЕКОТОРЫХ известных звёзд Мировая практика выбора конструкций ВЭУ, их влияние на экономические характеристикии выбор ВЭУ для России
Мировая практика выбора конструкций ВЭУ, их влияние на экономические характеристикии выбор ВЭУ для России Помилуй! И помилован будешь…
Помилуй! И помилован будешь… «1С:Предприятие 8. Медицина. Клиническая лаборатория»
«1С:Предприятие 8. Медицина. Клиническая лаборатория» Нумерация в пределах тысячи
Нумерация в пределах тысячи