вебинар_финал

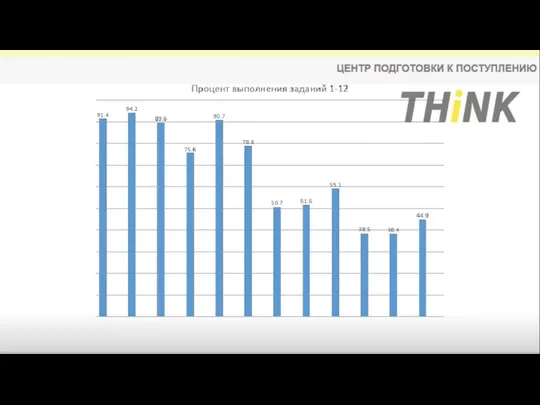
Немного статистики.
Средний балл участников вырос по сравнению с прошлым годом почти на 1 балл и составил 47,1 балла. Число участников, которым не удалось преодолеть минимальный порог в 27 баллов, сократилось на 1%. Всего в ЕГЭ по профильной математике приняли участие около 391 тысячи участников
РИА Новости
ЕГЭ по математике. Профиль.

Задание 1.
Это простая текстовая задача.
Что вам пригодится? Знание о том, что такое проценты, умение находить процент от числа, умение находить число по известной части.
Самое важное – внимательно прочитать условие, понять, придется ли округлять ответ.
Приведу пару интересных задач. Разбирать мы их не будем, но с ними полезно познакомиться.

Прототипы задания №1
Александр купил американский автомобиль, спидометр которого показывает скорость в милях в час. Какова скорость автомобиля в километрах в час, если спидометр показывает 75 миль в час? Считайте, что 1 миля равна 1609 м. Ответ округлите до целого числа.
Показания счётчика электроэнергии 1 ноября составляли 13465 кВт/ч, а 1 декабря — 14300 кВт/ч. Сколько нужно заплатить за электроэнергию за ноябрь, если 1 кВт/ч электроэнергии стоит 2 рубля 70 копеек? Ответ дайте в рублях.
Рост человека 7 футов 2 дюйма. Выразите его рост в сантиметрах, если 1 фут равен 12 дюймам. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа сантиметров.
На бензоколонке один литр бензина стоит 37 руб. 60 коп. Водитель залил в бак 30 литров бензина и купил бутылку воды за 65 рублей. Сколько рублей сдачи он получит с 2000 рублей?
На одну порцию рисовой каши требуется 35 грамм риса и 0,09 литра молока. Какое наибольшее количество порций каши может приготовить столовая, если в ее распоряжении есть 900 грамм риса и 3 литра молока?
Розничная цена учебника 160 рублей, она на 25% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 15 000 рублей?

Задание 2.
Со вторым заданием справляются практически все выпускники: самое важное понимать, что именно нужно найти, верно «прочитать» график или диаграмму, проверить, в каких единицах измерений нужно дать ответ.
В качестве примеров приведу несколько заданий, которые могут вас встретиться.

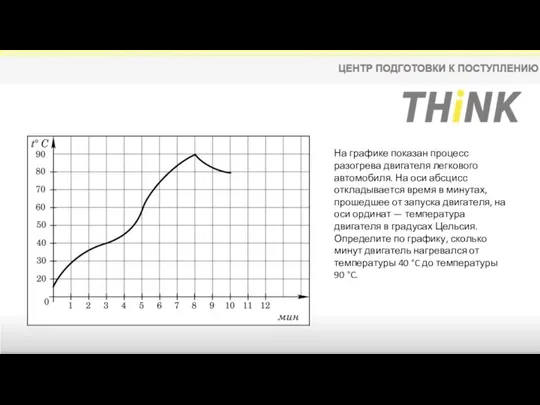
На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры 40 °C до температуры 90 °C.

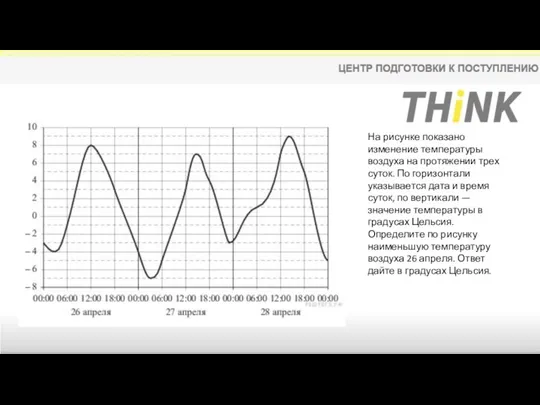
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 26 апреля. Ответ дайте в градусах Цельсия.

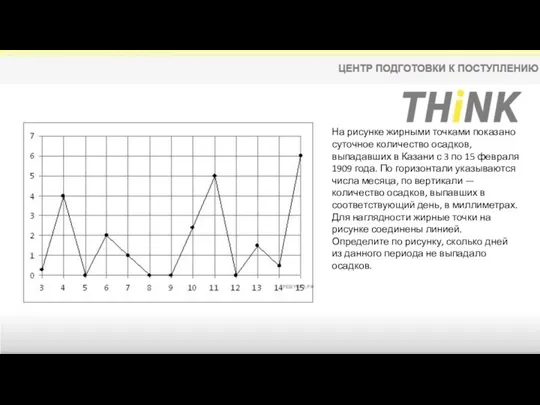
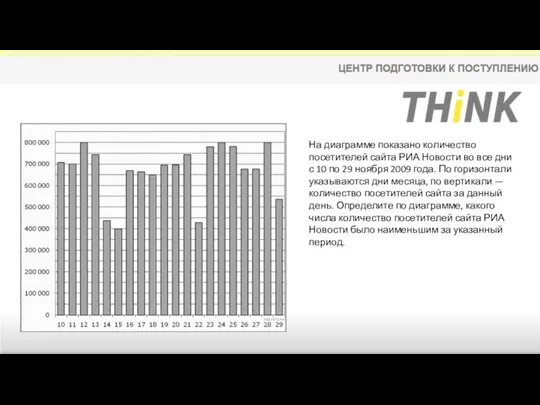
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода не выпадало осадков.

На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, какого числа количество посетителей сайта РИА Новости было наименьшим за указанный период.

Задание 3.
Пожалуй, это первое задание, которое может вызвать затруднения.
Что нужно знать для решения этого задания?
Как вычислять длины
Как вычислять углы
Как работать с координатной плоскостью
Окружность, круг
Тригонометрические функции: синус угла, косинус угла, тангенс угла, котангенс угла
Площади фигур: треугольник, четырехугольник, многоугольник, круг, сектор
Длина окружности, длина дуги окружности, периметр многоугольников
Формула Пика
Рассмотрим некоторые прототипы задач.

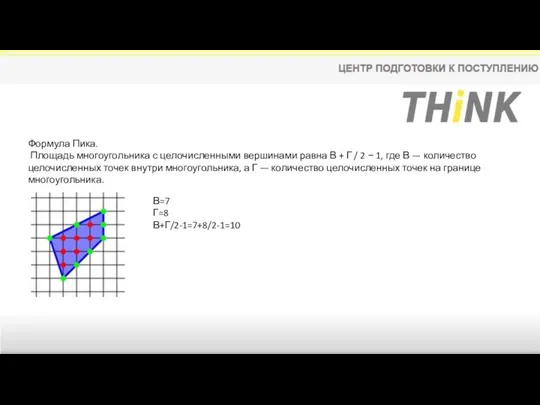
Формула Пика.
Площадь многоугольника с целочисленными вершинами равна В + Г / 2 − 1, где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
В=7
Г=8
В+Г/2-1=7+8/2-1=10

Найдите площадь закрашенной фигуры на координатной плоскости.
Чтобы найти площадь закрашенной фигуры, нужно найти разницу между площадями большого и маленького ромбов.
Вспомним, что площадь ромба равна S=1/2*d1*d2
Итак,

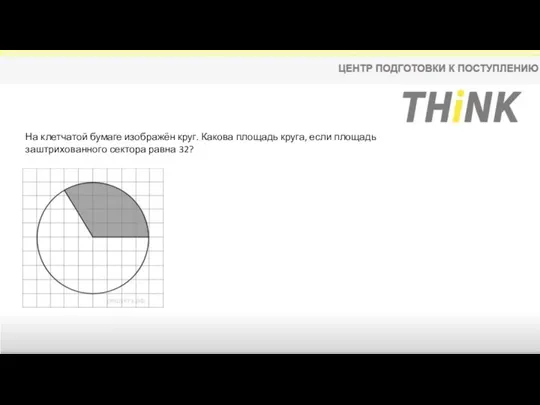
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?

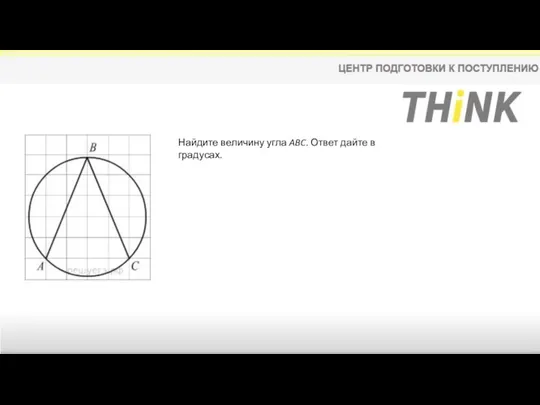
Найдите величину угла ABC. Ответ дайте в градусах.

Задание 4.
Теория вероятностей.
В отличие от первых трех заданий, эта задача поддается лишь ¾ ребят, которые сдают экзамен.
Но, на самом деле, задача несложная, главное, запомнить несколько фактов и научиться ими пользоваться:
Определение вероятности
Правило суммы
Правило произведения
Понятие зависимых и независимых событий
Диаграммы Эйлера-Венна
Полная вероятность
Формула Байеса

Рассмотрим несколько примеров задач на вероятность.
Фабрика выпускает сумки. В среднем 11 сумок из 160 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов. Результат округлите до сотых.
При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?
На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.

Решение:
Р= (160-11)/160=149/160=0,931…=0,93
Р= 18/(2982+18)=18/3000=0,006
Р= 3/10=0,3
Р= 2/6=0,33

Задание 5.
Если говорить о первых заданиях, пятое, пожалуй, требует наибольшего объема знаний для гарантированного решения.
Это и умение решать линейные, квадратные и кубические уравнения. И умение решать рациональные уравнения. Пригодятся знания о простейших тригонометрических уравнениях, логарифмах, ОДЗ, показательных уравнениях.
Но, несмотря на необходимость знать достаточно много о тех или иных типах уравнений, пятое задание не представляет больших сложностей, т.к. уравнения вполне простые и не требуют длительного счета.

Задание 6.
В ЕГЭ всего несколько заданий посвящено геометрии и стереометрии: 3, 6, 8, 14, 16.
Представьте, сколько разнообразных фактов вам может встретиться в 6ом задании, если весь учебник по планиметрии за 7-9 класс попробовать уместить в одном задании!
Очень сложно прогнозировать, что именно пригодится вам на самом экзамене, но, при этом, достаточно легко обобщить, что нужно уметь и что нужно знать для решения этого задания.
Элементы треугольника, виды треугольников, свойства биссектрисы, высоты, медианы
Четырехугольник: виды, свойства
Формулы площадей
Круг, окружность, вписанные и центральные углы, касательные
Вписанные и описанные окружности

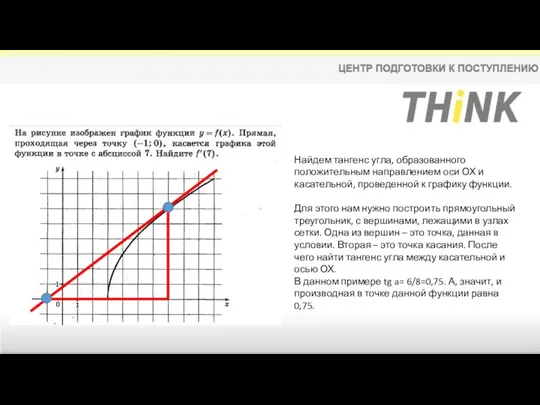
Задание 7
Седьмое задание посвящено производной и первообразной функции.
Что нужно знать для решения этой задачи?
Определение производной.
Физический смысл производной.
Геометрический смысл производной.
Уравнение касательной.
Таблица производных.
Производная суммы, разности, произведения, частного двух функций.
Производная сложной функции.
Связь производной функции и экстремумов.
Определение первообразной.
Физический смысл первообразной, площадь подграфика функции.

Найдем тангенс угла, образованного положительным направлением оси ОХ и касательной, проведенной к графику функции.
Для этого нам нужно построить прямоугольный треугольник, с вершинами, лежащими в узлах сетки. Одна из вершин – это точка, данная в условии. Вторая – это точка касания. После чего найти тангенс угла между касательной и осью ОХ.
В данном примере tg a= 6/8=0,75. А, значит, и производная в точке данной функции равна 0,75.

К сожалению, углубляться в задачи с производными сейчас не представляется возможным, так как в общеобразовательных школах эта тема начинается лишь в 11 классе.
Поэтому уточню, что понятие производной понадобится нам при сдаче ЕГЭ еще в 12 задании и, возможно, пригодится для решения задачи с параметром.

Задание 8
В восьмой задаче мы столкнемся с необходимостью решать стереометрическую задачу. Какие знания нам потребуются?
Понимание свойств, в первую очередь, следующих геометрических фигур:
Куб,
Прямоугольный параллелепипед,
Составные многогранники,
Призма,
Пирамида,
Цилиндр,
Конус,
Шар.

Умение находить площади поверхностей и объемы вышеперечисленных фигур
Понимать, как строятся те или иные сечения и какими свойствами они обладают
Закон Архимеда и понимание его, а точнее связь между объемом погруженного в жидкость тела и объемом вытесненной жидкости.
Является ли восьмое задание сложным? Для среднестатистического школьника – пожалуй, да. К сожалению, лишь чуть более половины выпускников справляются с этим заданием.
Рассмотрим несколько прототипов.

1. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см3.
2300 см3 соответствуют 25 см воды, значит, в 1 см находится объем 2300:25. Уровень воды изменился на 2 см, значит, объем детали – 2300:25*2=184 см3

2. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Площадь основания отсеченной части меньше площади основания всей призмы в 4 раза (так как и высота и основание треугольника уменьшились в 2 раза). Высота осталась прежней, следовательно, объем уменьшился в 4 раза.

3. Найдите объем части конуса, изображенной на рисунке. В ответе укажите V/π.

Задание 9.
Общая идея этой задачи – насколько хорошо вы усвоили за школьный курс:
как вычислять значения выражений
как их преобразовывать
как работать со степенями чисел
что такое логарифмы, их свойства
как работать с тригонометрическими выражениями и тождествами
умение использовать формулы сокращенного умножения
понимание того, как складываются, умножаются многочлены
Небольшая подсказка: в бланке ответов ЕГЭ можно записать целое число или десятичную дробь, поэтому будьте внимательны!

Задание 10.
Чем ближе к концу первой части экзамена, тем сложнее для большинства становятся задачи.
Десятое задание проверяет, насколько хорошо вы умеете работать с формулами, понимать из условия, какие буквы что обозначают, выражать неизвестную переменную через известные, ну и напоследок вычислять те или иные значения выражений.
Приведу пример одной из наиболее сложных, на мой взгляд, задач.

Задание 11.
Если говорить современным языком: «Это фиаско, братан!»
Почему?
Объективная причина – с этой задачей справляется лишь около 40% сдающих экзамен. Это наименее решаемая задача в первой части.
С чем это связано? Полагаю с тем, что в школе совершенно забывают о том, что математика – это язык. А значит, любая текстовая задача, которая, по сути, является лишь переводом условия с обычного языка на математический, становится камнем преткновения выпускников на экзамене.

Что нужно для решения 11ой задачи?
Умение по условию задачи составить уравнение или систему уравнений.
Решить получившееся уравнение или систему.
При этом, по трудозатратам первый пункт на порядок сложнее второго. Потому что для решения уравнений или систем у вас в голове уже всё готово!
Давайте приведем примеры наиболее сложных задач из прототипов экзамена.

Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?

2. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.

3. Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

4. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

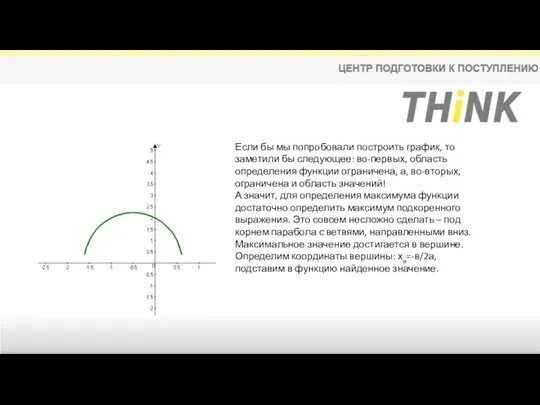
Задание 12.
Это задание обобщает знания о производной. Т.к. в данный момент большинство из вас с ней по школьной программе еще не знакомы, остановимся на рассмотрении задачи, которую можно решить без применения производной для исследования функции.

Если бы мы попробовали построить график, то заметили бы следующее: во-первых, область определения функции ограничена, а, во-вторых, ограничена и область значений!
А значит, для определения максимума функции достаточно определить максимум подкоренного выражения. Это совсем несложно сделать – под корнем парабола с ветвями, направленными вниз. Максимальное значение достигается в вершине. Определим координаты вершины: хв=-в/2а, подставим в функцию найденное значение.

За первую часть вы можете набрать 12 первичных баллов – в пересчете это 62 вторичных балла. Это, конечно, невысокий результат, но для поступления на многие специальности – вполне достаточный.
Конечно, вторая часть экзамена гораздо сложнее, с одной стороны, и требует гораздо большего времени для подготовки, но она еще и гораздо интереснее для решения!
Для подготовки могу посоветовать следующее:
https://ege.sdamgia.ru/ - в качестве тренажера первой части
http://85.142.162.119/os11/xmodules/qprint/index.php?proj=AC437B34557F88EA4115D2F374B0A07B – открытый банк заданий ЕГЭ ФИПИ
Сборник задач по математике для поступающих в вузы под редакцией М.И. Сканави
Задачи с параметрами при подготовке к ЕГЭ. Высоцкий В.С.
https://www.mccme.ru/prasolov/ - страница автора учебников и задачников по геометрии
Сборник экономических задач под редакцией Кулабухова, Лысенко