Слайд 2Жизнь и деятельность Евклида
Евклид (предположитель-но 330-277 до н.э.) - математик Александрийской школы

Древней Греции, автор первого дошедшего до нас трактата по математике.
Слайд 4Пять постулатов Евклида
От всякой точки до всякой другой точки возможно провести только

одну прямую линию.
Ограниченную прямую линию возможно непрерывно продолжать по прямой .
Из всякого центра и всяким раствором возможно описать круг.
Все прямые углы равны между собой
Если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные эти две прямые неограниченно встречаются с той стороны, где углы меньше двух
Слайд 5Пятый постулат
Если прямая, падающая на две прямые, образует внутренние и по одну

сторону углы, меньшие двух прямых, то продолженные эти две прямые неограниченно встречаются с той стороны, где углы меньше двух прямых.
Слайд 6V постулат о параллельных формулировали:
Прокл (411 - 485 до н.э.)
Евклид

(325 - 265 до н.э.)
Архимед (287 - 212 до н.э.)
Птолемей (85 - 165 до н.э.)
Валлис (1663)
Лежандр (1794, 1823),
и даже известный поэт Омар Хайям
Но 'крёстным дедом' неевклидовой геометрии оказался итальянский монах, учивший математике и грамматике Джироламо Саккери, известный предсмертным трактатом (1766):
"Евклид, очищенный от всех пятен".
Слайд 79 аксиом Евклида
Равные одному и тому же равны и между собой
Если

к равным прибавляют равные, то и целые будут равны
Если от равных отнимаются равные, то и остатки будут равны
Если к неравным прибавляют равные, то и целые будут не равны
Слайд 89 аксиом Евклида(продолжение)
Удвоенные одного и того же равны между собой
Половины одного

и того же равны между собой
Совмещающиеся один с другим равны между собой
Целое больше части
Две прямые не содержат пространства
Слайд 9Заключение
В арифметике Евклид сделал три значительных открытия. Во-первых, он сформулировал (без доказательства)

теорему о делении с остатком. Во-вторых, он придумал "алгоритм Евклида" - быстрый способ нахождения наибольшего общего делителя чисел или общей меры отрезков (если они соизмеримы). Наконец, Евклид первый начал изучать свойства простых чисел - и доказал, что их множество бесконечно. Но правда ли, что любое целое число разлагается в произведение простых чисел единственным способом? Доказать это Евклид не сумел - хотя располагал всеми необходимыми для этого средствами.








 История развития гидравлики
История развития гидравлики Теория детской игры Эльконина Даниила Борисовича
Теория детской игры Эльконина Даниила Борисовича Қисық11А
Қисық11А Электроэнергетика 10 класс
Электроэнергетика 10 класс Народные промыслы России
Народные промыслы России Климат - сервис
Климат - сервис Презентация на тему Израиль
Презентация на тему Израиль  ООО Завод Модульных Конструкций - один из крупнейших в РФ, по изготовлению Блок контейнеров
ООО Завод Модульных Конструкций - один из крупнейших в РФ, по изготовлению Блок контейнеров Гуторова Олеся Ивановна. Диплом
Гуторова Олеся Ивановна. Диплом Врожденный гипотиреоз
Врожденный гипотиреоз 08. Произведение вектора на число
08. Произведение вектора на число Презентация на тему Лекарства и их виды
Презентация на тему Лекарства и их виды  Армия Казахстана
Армия Казахстана Итоги работы отрасли и основные направления инновационного развития легкой промышленности
Итоги работы отрасли и основные направления инновационного развития легкой промышленности Лекция 4 - Вывод нелинейных УУН для сети переменного тока
Лекция 4 - Вывод нелинейных УУН для сети переменного тока БИОЛОГИЯ И ПАТОЛОГИЯ РЫБ
БИОЛОГИЯ И ПАТОЛОГИЯ РЫБ Лёгкая атлетика. Прыжки в длину
Лёгкая атлетика. Прыжки в длину Транспорт России
Транспорт России Зоологический музей имени Э.А. Эверсмана
Зоологический музей имени Э.А. Эверсмана Дело о трех картах
Дело о трех картах День европейский языков
День европейский языков Лот 13, г. Хабаровск, ул. Сысоева, 21, кв. 19
Лот 13, г. Хабаровск, ул. Сысоева, 21, кв. 19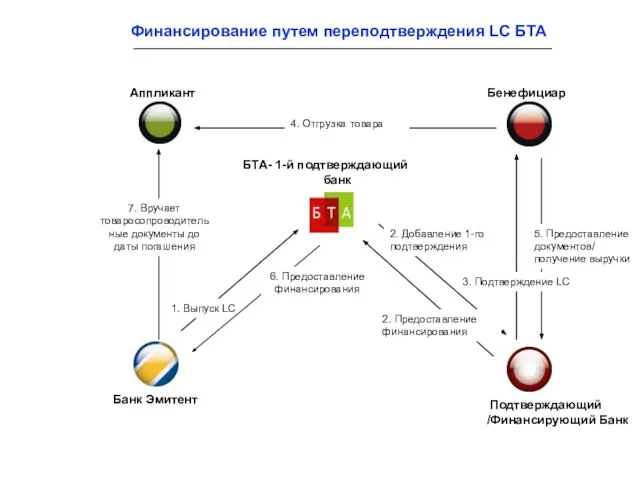 Финансирование путем переподтверждения LC БТА
Финансирование путем переподтверждения LC БТА Звіт основні орієнтири 2 клас 2013
Звіт основні орієнтири 2 клас 2013 Презентация на тему Бунге - министр финансов
Презентация на тему Бунге - министр финансов 04.07.201204.07.2012Eurasia - Institut EURASIA Institute, Berlin. - презентация
04.07.201204.07.2012Eurasia - Institut EURASIA Institute, Berlin. - презентация ХАНС ХОЛЬБЕН МЛАДШИЙ
ХАНС ХОЛЬБЕН МЛАДШИЙ Цветок
Цветок