Слайд 2Consider the line y=3x
Now rotate the line 360° about the x axis
.
As

you can see the result is a solid cone. The volume of the cone can be thought of as a series of discs or cylinders.
Слайд 3Volume of a cylinder
The volume of a cylinder is the area of

the circular cross-section multiplied by the height.
The area of a circle is πr2
The height is h
So V= πr2h
We can think of a disc
as a very thin cylinder
Слайд 4Consider a small disc in the cone
The volume of the disc is

the area of the circular cross-section multiplied by the height (or length in our case).
Now the radius of the circular cross-section is y and the length of the disc is δx.
So V=πy2δx
Слайд 5Integration as a process of summation
We have seen that integration is a

process of summation that adds a series of very small strips to give an area.
This process can also be used to add a series of very small discs.
As with areas, as δx→0, the limit of the sum gives the result that the volume of revolution about the x axis is given by
Слайд 6Volumes of revolution example
As with area, vertical boundaries can be added in

the form of limits:
Слайд 7General formula
So the Volume of Revolution between the limits of x=a and

x=b about the x axis can be found with
Similarly, the Volume of Revolution between the limits of y=a and y=b about the y axis can be found with
Слайд 8Example 1
Find the volume generated when the area defined by the following

inequality is rotated completely about the x axis:
Слайд 9Example 1 Solution
So our four boundary equations are:
x-axis
curve
x-axis intercept
x-axis intercept

Слайд 10Example 1 Solution
Hence the volume of revolution is:

Слайд 11Example 2
Find the volume generated when the area defined by the following

inequalities is rotated completely about the y axis:
Слайд 12Example 2 Solution
So our four boundary equations are:
y-axis
curve
y-axis intercept
line
Since we are integrating

wrt y we need the equation of the curve in terms of x2.











 Деловое платье - признак хорошего чувства стиля.
Деловое платье - признак хорошего чувства стиля. Партнерская программа teXet ЗАО «Электронные системы «Алкотел»
Партнерская программа teXet ЗАО «Электронные системы «Алкотел» Презентация
Презентация Современные информационные технологии в науке и технике. Конференция. Нижегородский институт управления
Современные информационные технологии в науке и технике. Конференция. Нижегородский институт управления Экспертная оценка конспекта урока по методике В.Д. Шадрикова
Экспертная оценка конспекта урока по методике В.Д. Шадрикова Блэкаут однотонный
Блэкаут однотонный ЗОЖ
ЗОЖ Презентация на тему Гигиена и правила ухода за кожей
Презентация на тему Гигиена и правила ухода за кожей Презентация на тему Appearance
Презентация на тему Appearance Модели за соработка и учество на локално ниво
Модели за соработка и учество на локално ниво День 1-й. АстроМагия – проработка гороскопа
День 1-й. АстроМагия – проработка гороскопа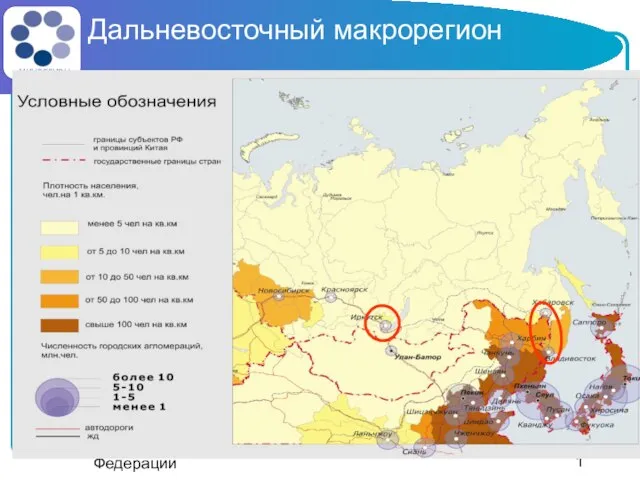 1
1 Презентация на тему Профессия программист
Презентация на тему Профессия программист  Энергоэффективные теплицы
Энергоэффективные теплицы Криминальная Россия 90-х. гг
Криминальная Россия 90-х. гг Распределенная информационная система сопровождения лечебной деятельности GEMO-SQL (2.03)
Распределенная информационная система сопровождения лечебной деятельности GEMO-SQL (2.03) Интеллектуальная разминка по Конституционному праву
Интеллектуальная разминка по Конституционному праву НОВАЯ СЕРИЯ УЧЕБНЫХ ПОСОБИЙ
НОВАЯ СЕРИЯ УЧЕБНЫХ ПОСОБИЙ Презентация на тему Визитная карточка школы
Презентация на тему Визитная карточка школы Раннее Возрождение (XIV - XV вв.) Филиппо Брунелески (1377-1446). История искусства. Часть 6
Раннее Возрождение (XIV - XV вв.) Филиппо Брунелески (1377-1446). История искусства. Часть 6 Реализация проектно-исследовательского метода
Реализация проектно-исследовательского метода Новые чудеса света 8 класс
Новые чудеса света 8 класс Дивеевская блаженная, Христа ради юродивая Пелагея Ивановна Серебренникова
Дивеевская блаженная, Христа ради юродивая Пелагея Ивановна Серебренникова ГИПЕРАКТИВНЫЕ РАССТРОЙСТВА(синдром дефицита внимания с гиперактивностью):клинико-психологическая сущность и ориентиры психол
ГИПЕРАКТИВНЫЕ РАССТРОЙСТВА(синдром дефицита внимания с гиперактивностью):клинико-психологическая сущность и ориентиры психол Расчет электрических нагрузок
Расчет электрических нагрузок Развитие эффективных отношений с инвесторами в преддверии IPO
Развитие эффективных отношений с инвесторами в преддверии IPO Бронза
Бронза Мониторинг заполнения дневников и журналов на сайте Эпос.Школа
Мониторинг заполнения дневников и журналов на сайте Эпос.Школа