Временная стоимость денег

2.1 Основы финансовых вычислений
Одним из важнейших свойств денежных потоков является их распределенность во времени.
При анализе относительно краткосрочных периодов ( до 1 года) в условиях стабильной экономики данное свойство оказывает относительно незначительное влияние, которым часто пренебрегают. Определяя годовой объем реализации по предприятию, просто складывают суммы выручки за каждый из месяцев отчетного года. Аналогично поступают со всеми остальными денежными потоками, что позволяет оперировать их итоговыми значениями.
Однако в случае более длительных периодов или в условиях сильной инфляции возникает серьезная проблема обеспечения сопоставимости данных. Одна и та же номинальная сумма денег, полученная предприятием с интервалом в 1 и более год, в таких условиях будет иметь для него неодинаковую ценность. Очевидно, что 1 млн. рублей в начале 1992 года был значительно весомее миллиона "образца" 1993 и более поздних лет. Как правило, в таких случаях производят корректировку отчетных данных с учетом инфляции. Но проблема не сводится только к учету инфляции. Одним из основополагающих принципов финансового менеджмента является признание временной ценности денег, то есть зависимости их реальной стоимости от величины промежутка времени, остающегося до их получения или расходования. В экономической теории данное свойство называется положительным временным предпочтением.

Наряду с инфляционным обесцениванием денег существует еще как минимум три важнейшие причины данного экономического феномена.
Во-первых, "сегодняшние" деньги всегда будут ценнее "завтрашних" из-за риска неполучения последних, и этот риск будет тем выше, чем больше промежуток времени, отделяющий получателя денег от этого "завтра".
Во-вторых, располагая денежными средствами "сегодня", экономический субъект может вложить их в какое-нибудь доходное предприятие и заработать прибыль, в то время как получатель будущих денег лишен этой возможности. Расставаясь с деньгами "сегодня" на определенный период времени (допустим, давая их взаймы на 1 месяц), владелец не только подвергает себя риску их невозврата, но и несет реальные экономические потери в форме неполученных доходов от инвестирования.
Кроме того, снижается его платежеспособность, так как любые обязательства, получаемые им взамен денег, имеют более низкую ликвидность, чем "живые" деньги. То есть у кредитора возрастает риск потери ликвидности, и это третья причина положительного временного предпочтения. Естественно, большинство владельцев денег не согласны бесплатно принимать на себя столь существенные дополнительные риски. Поэтому, предоствляя кредит, они устанавливают такие условия его возврата, которые, по их мнению, полностью возместят им все моральные и материальные неудобства, возникающие у человека, расстающегося (пусть даже и временно) с денежными знаками.

Количественной мерой величины этого возмещения является процентная ставка. С ее помощью может быть определена как будущая стоимость "сегодняшних" денег , так и настоящая стоимость "завтрашних" денег – например, тех, которыми обещают расплатиться через год после поставки товаров или оказания услуг.
Будущая стоимость – это операции наращения, поэтому будущую стоимость денег часто называют наращенной.
(например, если их собираются ссудить)
Текущая стоимость (современная, текущая или приведенная ) – это процесс дисконтирования или приведение будущей стоимости к ее современной величине (текущему моменту) – отсюда термин дисконтированная, приведенная или текущая стоимость.

Дисконтирование
Операции наращения денег по процентной ставке более просты и понятны, так как с ними приходится сталкиваться довольно часто беря или давая деньги взаймы. Однако для финансового менеджмента значительно более важное значение имеет дисконтирование денежных потоков, приведение их будущей стоимости к современному моменту времени для обеспечения сопоставимости величины распределенных по времени платежей.
Дисконтирование – это наращение "наоборот", однако для финансовых расчетов важны детали, поэтому необходимо более подробно рассмотреть как прямую, так и обратную задачу процентных вычислений. Прежде чем рассматривать их применительно к денежным потокам, следует усвоить наиболее элементарные операции с единичными суммами (разовыми платежами).

Процентная ставка показывает степень интенсивности изменения стоимости денег во времени.
Абсолютная величина этого изменения называется процентом, измеряется в денежных единицах (например, в рублях) и обозначается I.
Если обозначить будущую сумму S, а современную (или первоначальную) P, то .
Процентная ставка i является относительной величиной, измеряется в десятичных дробях или %, и определяется делением процентов на
первоначальную сумму: (1)

Можно заметить, что формула расчета процентной ставки идентична расчету статистического показателя "темп прироста".
Действительно, если абсолютная сумма процента (I) представляет собой прирост современной величины, то отношение этого прироста к самой современной величине и будет темпом прироста первоначальной суммы.
Наращение первоначальной суммы по процентной ставке называется декурсивным методом начисления процентов.
Кроме процентной существует учетная ставка d, (другое название – ставка дисконта), величина которой определяется по формуле:
(2) где D – сумма дисконта.

Сравнивая формулы (1) и (2) можно заметить, что сумма процентов I и величина дисконта D определяются одинаковым образом – как разница между будущей и современной стоимостями. Однако, смысл, вкладываемый в эти термины неодинаков.
Если в первом случае речь идет о приросте текущей стоимости, своего рода "наценке", то во втором определяется снижение будущей стоимости, "скидка" с ее величины. (Diskont в переводе с немецкого означает "скидка").
Неудивительно, что основной областью применения учетной ставки является дисконтирование, процесс, обратный по отношению к начислению процентов. Тем не менее, иногда она используется и для наращения. В этом случае говорят об антисипативных процентах.

При помощи рассмотренных выше ставок могут начисляться как простые так и сложные проценты. При начислении простых процентов наращение первоначальной суммы происходит в арифметической прогрессии, а при начислении сложных процентов – в геометрической. Вначале более подробно рассмотрим операции с простыми процентами.
Начисление простых декурсивных и антисипативных процентов производится по различным формулам:
Декурсивные проценты:
(3)
Антисипативные проценты:
(4)
Где n - продолжительность ссуды, измеренная в годах.

Для упрощения вычислений вторые сомножители в формулах (3) и (4) называются множителями наращения простых процентов - множитель наращения декурсивных процентов;
- множитель наращения антисипативных процентов.
Пример. Ссуда в размере 1 млн. рублей выдается сроком на 0,5 года под 30% годовых. В случае декурсивных процентов наращенная сумма ( ) будет равна 1,15 млн. рублей (1 * (1 + 0,5 * 0,3), а сумма начисленных процентов ( I ) - 0,15 млн. рублей (1,15 – 1). Если же начислять проценты по антисипативному методу, то наращенная величина ( ) составит 1,176 млн. рублей (1 * (1 / (1 – 0,5 * 0,3), а сумма процентов ( D ) 0,176 млн. рублей. Наращение по антисипативному методу всегда происходит более быстрыми темпами, чем при использовании процентной ставки. Поэтому банки используют этот метод для начисления процентов по выдаваемым ими ссудам в периоды высокой инфляции. Однако у него есть существенный недостаток: как видно из формулы (4), при знаменатель дроби обращается в нуль и выражение теряет смысл.

Начисление процентов с использованием ставки, предназначенной для выполнения прямо противоположной операции –дисконтирования – имеет оттенок некой "неестественности" и иногда порождает неразбериху (аналогичную той, которая может возникнуть у розничного торговца, если он перепутает правила определения скидок и наценок на свои товары). С позиции математики никакой сложности здесь нет, преобразовав (1), (2) и (4), получаем:
(5)
Соблюдая это условие, можно получать эквивалентные результаты, начисляя проценты как по формуле (3), так и по формуле (4).

Как правило, процентные ставки устанавливаются в годовом исчислении, поэтому они называются годовыми. Особенностью простых процентов является то, что частота процессов наращения в течение года не влияет на результат. То есть нет никакой разницы начислять 30% годовых 1 раз в год или начислить 2 раза по 15% годовых. Простая ставка 30% годовых при одном начислении в году называется эквивалентной простой ставке 15% годовых при начислении 1 раз в полгода. Данное свойство объясняется тем, что процесс наращения по простой процентной ставке представляет собой арифметическую прогрессию с первым членом и разностью

Наращенная сумма S есть ничто иное как последний k-й член этой прогрессии ( ), срок ссуды n равен . Поэтому, если увеличить n и одновременно пропорционально уменьшить i , то величина каждого члена прогрессии, в том числе и последнего, останется неизменной.
Однако продолжительность ссуды (или другой финансовой операции, связанной с начислением процентов) n необязательно должна равняться году или целому числу лет. Напротив, простые проценты чаще всего используются при краткосрочных (длительностью менее года) операциях. В этом случае возникает проблема определения длительности ссуды и продолжительности года в днях. Если обозначить продолжительность года в днях буквой K этот показатель называется временная база), а количество дней пользования ссудой t, то использованное в формулах (3) и (4) обозначение количества полных лет n можно будет выразить как

Подставив это выражение в (3) и (4), получим:
для декурсивных процентов: (6)
для антисипативных процентов: (7)

Наиболее часто встречаются следующие комбинации временной базы и длительности ссуды (цифры в скобках обозначают соответственно величину t и K ):
Точные проценты с точным числом дней (365/365).
Обыкновенные (коммерческие) проценты с точной длительностью ссуды (360/365).
Обыкновенные (коммерческие) проценты с приближенной длительностью ссуды (360/360).

Различия в способах подсчета дней могут показаться несущественными, однако при больших суммах операций и высоких процентных ставках они достигают весьма приличных размеров. Предположим, что ссуда в размере 10 млн. рублей выдана 1 мая с возвратом 31 декабря этого года под 45% годовых (простая процентная ставка). Определим наращенную сумму этого кредита по каждому из трех способов.
Табличное значение точной длительности ссуды равно 244 дня (365 – 121); приближенная длительность – 241 день (6 * 30 + 30 + 30 + 1).
10 * (1 + 0,45 * 244/365) = 13,008 млн. рублей
10 * (1 + 0,45 * 244/360) = 13,05 млн. рублей
10 * (1 + 0,45 * 241/360) = 13,013 млн. рублей
Разница между наибольшей и наименьшей величинами (13,05 – 13,008) означает, что должник будет вынужден заплатить дополнительно 42 тыс. рублей только за то, что согласился (или не обратил внимания) на применение 2 способа начисления процентов.

Обратной задачей по отношению к начислению процентов является расчет современной стоимости будущих денежных поступлений (платежей) или дисконтирование. В ходе дисконтирования по известной будущей стоимости S и заданным значениям процентной (учетной) ставки и длительности операции находится первоначальная ( современная, приведенная или текущая ) стоимость P. B зависимости от того, какая именно ставка – простая процентная или простая учетная – применяется для дисконтирования, различают два его вида: математическое дисконтирование и банковский учет.
Метод банковского учета получил свое название от одноименной финансовой операции, в ходе которой коммерческий банк выкупает у владельца (учитывает) простой или переводный вексель по цене ниже номинала до истечения означенного на этом документе срока его погашения. Разница между номиналом и выкупной ценой образует прибыль банка от этой операции и называется дисконт (D). Для определения размера выкупной цены (а следовательно, и суммы дисконта) применяется дисконтирование по методу банковского учета. При этом используется простая учетная ставка d.

Выкупная цена ( современная стоимость ) векселя определяется по формуле:
(8)
Где t - срок, остающийся до погашения векселя, в днях. Второй сомножитель этого выражения называется дисконтным множителем банковского учета по простым процентам. Как правило, при банковском учете применяются обыкновенные проценты с точной длительностью ссуды (2 вариант). Например, владелец векселя номиналом 25 тыс. рублей обратился в банк с предложением учесть его за 60 дней до наступления срока погашения. Банк согласен выполнить эту операцию по простой учетной ставке 35% годовых. Выкупная цена векселя составит:
А сумма дисконта будет равна:

2. При математическом дисконтировании используется простая процентная ставка i. Расчеты выполняются по формуле: (9).
Выражение называется дисконтным множителем математического дисконтирования по простым процентам.
Этот метод применяется во всех остальных (кроме банковского учета ) случаях, когда возникает необходимость определить современную величину суммы денег, которая будет получена в будущем. Например, покупатель обязуется оплатить поставщику стоимость закупленных товаров через 90 дней после поставки в сумме 1 млн. рублей. Уровень простой процентной ставки составляет 30% годовых (обыкновенные проценты). Следовательно текущая стоимость товаров будет равна:
Применив к этим условиям метод банковского учета, получим:

Основной областью применения простых процентной и учетной ставок являются краткосрочные финансовые операции, длительность которых менее 1 года. Вычисления с простыми ставками не учитывают возможность реинвестирования начисленных процентов, потому что наращение и дисконтирование производятся относительно неизменной исходной суммы P или S. В отличие от них сложные ставки процентов учитывают возможность реинвестирования процентов, так как в этом случае наращение производится по формуле не арифметической, а геометрической прогрессии, первым членом которой является начальная сумма P, а знаменатель равен
Где число лет ссуды n меньше числа членов прогрессии k на
Наращенная стоимость (последний член прогрессии) находится по формуле:
(10),
где множитель наращения декурсивных сложных процентов.

С позиций финансового менеджмента использование сложных процентов является более предпочтительным, т.к. признание возможности собственника в любой момент инвестировать свои средства с целью получения дохода является краеугольным камнем всей финансовой теории. При использовании простых процентов эта возможность часто не учитывается, поэтому результаты вычислений получаются менее корректными. Тем не менее при краткосрочных финансовых операциях по-прежнему широко применяются вычисления простых процентов. Некоторые математики считают это досадным пережитком, оставшимся с тех пор, когда у финансистов не было под рукой калькуляторов и они были вынуждены прибегать к более простым, хотя и менее точным способам расчета. Представляется возможным и несколько иное объяснение данного факта. При длительности операций менее 1 года начисление простых процентов обеспечивает получение результатов даже более выгодных для кредитора, чем использование сложных процентов. Выше уже отмечалась закономерность выбора банками именно таких, более выгодных для кредитора способов. Поэтому было бы наивно недооценивать вычислительные мощности современных банков и интеллектуальный потенциал их сотрудников, полагая, что они используют грубые методы расчетов только из-за их низкой трудоемкости.

Сама по себе сложная процентная ставка i ничем не отличается от простой и рассчитывается по такой же формуле (1). Сложная учетная ставка определяется по формуле (2). Так же как и в случае простых процентов возможно применение сложной учетной ставкидля начисления процентов (антисипативный метод):
(11)
где - множитель наращения сложных антисипативных процентов.
*Однако практическое применение такого способа наращения процентов весьма ограничено и он относится скорее к разряду финансовой экзотики.

Как уже отмечалось, наиболее широко сложные проценты применяются при анализе долгосрочных финансовых операций . На большом промежутке времени в полной мере проявляется эффект реинвестирования, начисления "процентов на проценты". В связи с этим вопрос измерения длительности операции и продолжительности года в днях в случае сложных процентов стоит менее остро. Как правило, неполное количество лет выражают дробным числом через количество месяцев (3/12 или 7/12), не вдаваясь в более точные подсчеты дней. Поэтому в формуле начисления сложных процентов число лет практически всегда обозначается буквой n, а не выражением t/K, как это принято для простых процентов. Наиболее щепетильные кредиторы, принимая во внимание большую эффективность простых процентов на коротких отрезках времени, используют смешанный порядок начисления процентов в случае, когда срок операции (ссуды) не равен целому числу лет: сложные проценты начисляются на период, измеренный целыми годами, а проценты за дробную часть срока начисляются по простой процентной ставке.

(12)
где a - число полных лет в составе продолжительности операции,
t – число дней в отрезке времени, приходящемся на неполный год,
K - временная база.
В этом случае вновь возникает необходимость выполнения календарных вычислений по рассмотренным выше правилам. Например, ссуда в 3 млн. рублей выдается 1 января 1997 года по 30 сентября 1999 года под 28% годовых (процентная ставка). В случае начисления сложных процентов за весь срок пользования деньгами наращенная сумма составит:
Если же использовать смешанный способ (например, коммерческие проценты с точным числом дней), то получим:
Таким образом, щепетильность кредитора в данном случае оказалась вовсе не излишней и была вознаграждена дополнительным доходом в сумме 85 тыс. рублей.

Важной особенностью сложных процентов является зависимость конечного результата от количества начислений в течение года. Здесь опять сказывается влияние реинвестирования начисленных процентов: база начисления возрастает с каждым новым начислением, а не остается неизменной, как в случае простых процентов. Например, если начислять 20% годовых 1 раз в год, то первоначальная сумма в 1 тыс. рублей возрастет к концу года до 1,2 тыс. рублей (1 * (1+ 0,2)). Если же начислять по 10% каждые полгода, то будущая стоимость составит 1,21 тыс. рублей (1 * (1 + 0,1) * (1 + 0,1)), при поквартальном начислении по 5% она возрастет до 1,216 тыс. рублей. По мере увеличения числа начислений (m) и продолжительности операции эта разница будет очень сильно увеличиваться. Если разделить сумму начисленных процентов при ежеквартальном наращении на первоначальную сумму, то получится 21,6% (0,216 / 1 * 100), а не 20%. Следовательно сложная ставка 20% при однократном наращении и 20% (четыре раза по 5%) при поквартальном наращении приводят к различным результатам, то есть они не являются эквивалентными. Цифра 20% отражает уже не действительную (эффективную), а номинальную ставку. Эффективной процентной ставкой является значение 21,6%. В финансовых расчетах номинальную сложную процентную ставку принято обозначать буквой j. Формула наращения по сложным процентам при начислении их m раз в году имеет вид:
(13)

Пример:
Ссуда размером 5 млн. рублей выдана на 2 года по номинальной сложной процентной ставке 35% годовых с начислением процентов 2 раза в год.
Будущая сумма к концу срока ссуды составит:
При однократном начислении ее величина составила бы лишь 9,113 млн. рублей (5 * (1 + 0,35)^2; зато при ежемесячном начислении возвращать пришлось бы уже 9,968 млн. рублей (5 * 1 + (0,35 / 12)^(12 * 2)).

При начислении антисипативных сложных процентов, номинальная учетная ставка обозначается буквой f , а формула наращения принимает вид: (14)
Выражение множитель наращения по номинальной учетной ставке. Дисконтирование по сложным процентам также может выполняться двумя способами – математическое дисконтирование и банковский учет. Последний менее выгоден для кредитора, чем учет по простой учетной ставке, поэтому используется крайне редко. В случае однократного начисления процентов, его формула имеет вид: (15), где - дисконтный множитель банковского учета по сложной учетной ставке, при получаем: (16), где f - номинальная сложная учетная ставка,
- – дисконтный множитель банковского учета по сложной номинальной учетной ставке.

Значительно более широкое распространение имеет математическое дисконтирование по сложной процентной ставке i. Для получаем
(17)
где - дисконтный множитель математического дисконтирования по сложной процентной ставке.
При неоднократном начислении процентов в течение года формула математического дисконтирования принимает вид:
(18)
где j - номинальная сложная процентная ставка,
- дисконтный множитель математического дисконтирования по сложной номинальной процентной ставке.

Пример:
Требуется определить современную стоимость платежа в размере 3 млн. рублей, который должен поступить через 1,5 года,процентная ставка составляет 40%:
при m=1
при m=2 (начисление 1 раз в полугодие)
при m=12 (ежемесячное начисление)

По мере увеличения числа начислений процентов в течение года (m) промежуток времени между двумя смежными начислениями уменьшается – при m=1 этот промежуток равен 1 году, а при m=12 - только 1 месяцу. Теоретически можно представить ситуацию, когда начисление сложных процентов производится настолько часто, что общее его число в году стремится к бесконечнности, тогда величина промежутка между отдельными начислениями будет приближаться к нулю, то есть начисление станет практически непрерывным. Такая на первый взгляд гипотетическая ситуация имеет важное значение для финансов и при построении сложных аналитических моделей (например при разработке масштабных инвестиционных проектов) часто применяют непрерывные проценты. Непрерывная процентная ставка (очевидно, что при непрерывном начислении речь может идти только о сложных процентах) обозначается буквой (читается "дельта"), часто этот показатель называют "сила роста". Формула наращения по непрерывной процентной ставке имеет вид:
(19)
где е - основание натурального логарифма ( )
- множитель наращения непрерывных процентов.

Вопрос.
Чему будет равна через 3 года сумма 250 тыс. рублей, если сегодня положить ее на банковский депозит под 15% годовых, начисляемых непрерывно?
Для непрерывных процентов не существует различий между процентной и учетной ставками – сила роста является универсальным показателем. Однако, наряду с постоянной силой роста может использоваться переменная процентная ставка, величина которой меняется по заданному закону (математической функции). В этом случае можно строить очень мощные имитационные модели, однако математический аппарат расчета таких моделей достаточно сложен и не рассматривается в настоящем пособии, так же как и начисление процентов по переменной непрерывной процентной ставке.

Непрерывное дисконтирование с использованием постоянной силы роста выполняется по формуле:
(20)
где дисконтный множитель дисконтирования по силе роста.
Пример:
В результате осуществления инвестиционного проекта планируется получить через 2 года доход в размере 15 млн. рублей. Чему будет равна приведенная стоимость этих денег в сегодняшних условиях, если сила роста составляет 22% годовых?

2.2 Элементарные финансовые расчеты
В условиях нестабильной экономики банки и другие кредиторы с целью снижения своего процентного риска могут устанавливать переменные ставки процентов для различных финансовых операций. Например, по ссуде в размере 2 млн. рублей общей продолжительностью 120 дней в течение первых двух месяцев будут начисляться 30% годовых, а начиная с 61 дня ежемесячно простая процентная ставка будет увеличиваться на 5% (обыкновенные проценты). Фактически, ссуда разбивается на несколько составляющих, по каждой из которых установлены свои условия. Необходимо найти наращенные суммы по каждой из составляющих, а затем сложить их. Вспомним, что аналогом процентной ставки в статистике является показатель "темп прироста". При начислении простых процентов следует говорить о базисных темпах прироста, т.к. первоначальная сумма P остается неизменной. Данная задача в статистических терминах может быть интерпретирована как сложение базисных темпов прироста с последующим умножением на первоначальную сумму займа. Общая формула расчета будет иметь следующий вид:
(1)
где N - общее число периодов, в течение которых проценты начисляются по неизменной ставке.

Подставив в это выражение условия нашего примера, получим:
(2)
Подставив условия примера, получим:
Данную задачу можно решить несколько иным путем – рассчитав сначала средние процентные ставки. Расчет средних процентных ставок (или расчет средних доходностей) вообще очень распространенная в финансах операция. Для ее выполнения полезно опять вспомнить о математико-статистической природе процентных ставок. Так как начисление простых процентов происходит в арифметической прогрессии, средняя простая ставка рассчитывается как средняя арифметическая взвешенная.

где N - общее число периодов, в течение которых процентная ставка оставалась неизменной
Сложные проценты растут в геометрической прогрессии, поэтому средняя сложная процентная ставка рассчитывается как средняя геометрическая взвешенная. В качестве весов в обоих случаях используются продолжительности периодов, для которых действовала фиксированная ставка.
(4)
Снова используем данные нашего примера. В случае начисления простых процентов получим:
(3)

То есть средняя процентная ставка составила 33,75% и начисление процентов по этой ставке за весь срок ссуды дает такой же результат, как и тот, что был получен по формуле (1). Для сложных процентов выражение примет вид:
Начисление процентов по средней процентной ставке 33,69% также дает результат, эквивалентный тому, что был получен по формуле(2).
Понимание различий механизмов наращения простых и сложных процентов помогает избегать довольно распространенных ошибок. Например, следует помнить, что такой процесс как инфляция развивается в геометрической, а не в арифметической прогрессии, то есть к нему должны применяться правила начисления сложных, а не простых процентов.

Темпы прироста цен в этом случае являются цепными, а не базисными, т.к. в каждом последующем месяце рост цен относится к предыдущему месяцу, а не к началу года или какой-либо иной неизменной базе.
Например, если инфляция в январе составила 5%, в феврале 4%, а в
марте 9%, то общая инфляция за квартал будет равна не 18% (сумма месячных показателей), а 19,03% (1,05 * 1,04 * 1,09 – 1). Среднемесячный уровень инфляции за этот квартал составит (1,05 * 1,04 * 1,09)1/3 - 1 = 5,98%. С другой стороны, если объявляется, что среднемесячная инфляция за год составила 5,98%, то это не значит, что общая инфляция за год в 12 раз больше (71,76%). На самом деле годовая инфляция в этом случае составит свыше 100,7% (1,059812 - 1).

В предыдущей лекции обращалось внимание на сложности, возникающие при попытке понять смысл антисипативного начисления процентов. Рассмотрим ситуацию, в которой необходимо прибегнуть именно к этому способу.
Пример: Коммерсант предлагает вместо оплаты наличными выписать на стоимость закупленных материалов вексель в сумме 500 тыс. рублей со сроком оплаты через 90 дней, который может быть учтен в банке по простой учетной ставке 25% годовых ( коммерческие проценты с точным числом дней ссуды). Для определения суммы, которую понадобится проставить в этом векселе ему необходимо начислить проценты на стоимость товаров, используя антисипативный метод. Сумма векселя составит 533,333 тыс. рублей (500 * 1 / (1 – 90 / 360 * 0,25). Если продавец в этот же день учтет этот вексель в банке (на оговоренных условиях), то получит на руки ровно 500 тыс. рублей (533,333 * (1 – 90 / 360 * 0,25)). Таким образом, начисление антисипативных процентов используется для определения наращенной суммы, которая затем будет дисконтироваться по той же самой ставке, по которой производилось начисление. Такое чисто техническое использование наращения по учетной ставке является преобладающим в практических расчетах.

Наряду с расчетом будущей и современной величины денежных средств часто возникают задачи определения других параметров финансовых операций: их продолжительности и величины процентной или учетной ставок. Например, может возникнуть вопрос: сколько времени понадобится, чтобы данная сумма при заданном уровне процентной ставки удвоилась, или при каком уровне учетной ставки в течение года исходная сумма возрастет в полтора раза? Решение подобных задач сводится к преобразованию соответствующей формулы наращения ( дисконтирования ) таким образом, чтобы вычислить значение неизвестного параметра. Например, если надо рассчитать продолжительность ссуды по известным первоначальной и будущей суммам, а также уровню простой процентной ставки, то преобразуя формулу начисления простых декурсивных процентов (S = P * (1 + ni)), получим формулу (5) из табл. 2.1 (Все формулы и их нумерация приведены в табл. 2.1). По такой же формуле будет определяться срок до погашения обязательства при математическом дисконтировании.

Определение срока финансовой операции для антисипативного начисления процентов и банковского учета производится по формуле(6) из табл. 2.1 Например, нужно определить через какой период времени произойдет удвоение суммы долга при начислении на нее 20% годовых простых а) при декурсивном методе начисления процентов; б) при использовании антисипативного метода. Временная база в обоих случаях принимается равной 365 дней (точные проценты). Применив формулы (5) и (6), получим:

Эти же формулы можно применить для определения срока до погашения обязательств при дисконтировании.
Пример: по векселю номиналом 700 тыс. рублей банк выплатил 520 тыс. рублей, произведя его учет по простой ставке 32% годовых. Чему равен срок до погашения векселя? Применив формулу (6), получим:
Товар, стоимостью 1,5 млн. рублей оплачивается на условиях коммерческого кредита, предоставленного под 15% годовых (простая процентная ставка, временная база 360 дней). Сумма оплаты по истечении срока кредита составила 1 млн. 650 тыс. рублей. Чему равен срок предоставленного кредита? Из формулы (5) следует:

Таблица 2.1. Формулы расчета продолжительности финансовых операций и процентных (учетных) ставок по ним

Пример:
сколько лет должен пролежать на банковском депозите под 20% (сложная процентная ставка i) вклад 100 тыс. рублей, чтобы его сумма составила 250 тыс. рублей?
Подставив данные в формулу (7), получим:
Если начисление процентов при этих же условиях будет производиться ежемесячно, то в соответствии с формулой (8):

Рассмотрим способы расчета величины процентных (учетных) ставок, когда заданы другие параметры финансовой операции. Преобразовав формулы декурсивного и антисипативного наращения простых процентов, получим выражения (12) и (13) в табл. 2.1). Например, чему будет равна простая процентная ставка по ссуде, выданной на 90 дней в размере 350 тыс. рублей, и возвращенной по истечении срока в сумме 375 тыс. рублей (временная база 360 дней)? Подставив эти данные в формулу (12), получим:
Вексель номиналом 1 млн. рублей учтен в банке за 60 дней до его погашения в сумме 900 тыс. рублей. По какой простой учетной ставке было произведено его дисконтирование? Используем для расчетов формулу (13):

Очевидно, что данная методика может (и должна) использоваться при анализе любых финансовых операций, а не только в процессе банковского кредитования. Например, иностранная валюта в объеме 1000 единиц, купленная по курсу 20 руб. за 1 единицу, через месяц была продана по курсу 20 руб. 50 коп. Определить доходность этой операции по годовой простой процентной ставке (коммерческие проценты ). Из формулы (12) получаем:

Аналогичный подход к расчету доходности используется и на фондовых рынках. Например, Центральным Банком России была рекомендована следующая формула расчета доходности ГКО:
(14)
где N – номинал облигации
P - цена ее приобретения
t - срок до погашения.
По сути дела она повторяет формулу (12) применительно к точным процентам (временная база 365 дней).

Пример:
Облигация номиналом 10 тыс. рублей была приобретена за 8,2 тыс. рублей за 40 дней до погашения. Ее годовая доходность, рассчитанная как простая процентная ставка, составит:
Точно такой же результат можно получить, применив формулу (12).

Не следует отождествлять процентную ставку, указываемую в кредитном договоре, с доходностью операции, рассчитанной в процентах.
В первом случае процентная ставка является реальным партнером финансовой операции, однозначно определяющим величину платежа, который должен последовать в случае исполнения договора.
Доходность – это производная величина, не определяющая, а определяемая теми денежными потоками, которые порождает кредитный договор (ценная бумага или другой финансовый инструмент). Доходность, в явной форме, не присутствует в ходе осуществления финансовой операции. Рассчитывая доходность финансовой операции, инвестор получает субъективную оценку ее величины, зависящую от целого ряда предпосылок, таких как способ начисления процентов, выбор временной базы и т.п. Эти предпосылки не являются объективными и неизбежными – при всем уважении к Центральному банку инвестор может определить доходность купленной им ГКО по ставке сложных, а не простых процентов, не нарушив при этом ни физических ни юридических законов (и поступив совершенно правильно с позиции финансовой теории).

Рекомендация вычислять доходность по методике наращения простых процентов используется на данном рынке как соглашение его участников (точно такое же как соглашение о подсчете точной временной базы). Выполнение условий этого соглашения гарантирует участникам рынка сопоставимость результатов их расчетов, т.е. помогает избежать путаницы, но не более этого.
Степень соответствия того либо иного метода расчета доходности идеалу в данном контексте не имеет значения – это предмет научных дискуссий. Используя неправильную или несовершенную методику расчета доходности, инвестор имеет все шансы достаточно быстро разориться, точно так же как и предприятие, завышающее прибыль, вследствие неправильного калькулирования издержек. Но конечной причиной банкротства станет отсутствие у него денег для покрытия обязательств, до этого момента ни один кредитор не сможет вчинить иск о банкротстве только на основании несогласия с методикой подсчета доходности, которой пользуется его должник.
Для финансового менеджмента сложные проценты имеют неизмеримо большую ценность, чем простые. Очевидно, что при использовании методики расчета простых процентов значение доходности искажается уже из-за того, что данная методика не учитывает возможности реинвестирования полученных доходов. Поэтому при прочих равных условиях безусловно предпочтительным является расчет доходности как ставки сложных процентов. Рассмотрим методику определения величины этой ставки, когда известны другие параметры финансовой операции. В результате преобразования исходных выражений наращения ( дисконтирования ) по сложным процентам, получим (см. (15) – (19) в табл. 2.1).

В качестве иллюстрации рассчитаем доходность облигации из предыдущего примера как ставку сложного процента (наращение 1 раз в году):
Этот результат более чем в 2,5 раза превышает доходность, рассчитанную как ставку простых процентов. Означает ли это, что инвестор, использующий для расчета доходности сложные проценты, в два с половиной раза богаче того, кто купив в один день с ним точно такую же облигацию, применяет для вычислений простые проценты? Тогда последнему следует срочно разучивать новую формулу и точно так же богатеть.
Однако, в случае сложных процентов не все так однозначно. Если рассчитывать доходность как сложную номинальную ставку (16), то ее уровень резко снизится, при получим:

При расчете доходности как силы роста – непрерывные проценты (19) – ее уровень будет более точно соответствовать тому, что был рассчитан с помощью простой процентной ставки:
Чтобы не запутаться в обилии методов расчета процентных ставок не обязательно зазубривать каждую формулу. Достаточно четко представлять, каким образом она получена. Кроме этого, следует помнить, что любому значению данной ставки может быть поставлено в соответствие эквивалентное значение какой-либо другой процентной или учетной ставки. В предыдущей лекции был приведен подобный пример эквивалентности между простыми процентной и учетной ставками (5).

Эквивалентными называются ставки, наращение или дисконтирование по которым приводит к одному и тому же финансовому результату.
Например, в условиях последнего примера эквивалентными являются простая процентная ставка 200,3% и сложная процентная ставка 511,6%, т.к. начисление любой из них позволяет нарастить первоначальную сумму 8,2 тыс. рублей до 10 тыс. рублей за 40 дней. Приравнивая между собой множители наращения ( дисконтирования ), можно получить несложные формулы эквивалентности различных ставок.
Для удобства эти формулы представлены в табличной форме. В заголовки граф табл. 2.2 помещены простые процентная (i) и учетная (d) ставки. В заголовках строк этой таблицы указаны все рассмотренные в данном пособии ставки. На пересечении граф и столбцов приводятся формулы эквивалентности соответствующих ставок. В таблицу не включены уравнения эквивалентности простых процентных и сложных учетных ставок, вследствие маловероятности возникновения необходимости в таком сопоставлении.

Таблица 2.2 Эквивалентность простых ставок

Пример:
Предприятие может столкнуться с необходимостью выбора между получением кредита на 5 месяцев под сложную номинальную ставку 24% (начисление процентов поквартальное) и учетом в банке векселя на эту же сумму и с таким же сроком погашения. Необходимо определить простую учетную ставку, которая сделает учет векселя равновыгодной операцией по отношению к получению ссуды. По формуле (26) получим
Кроме формул, приведенных в табл. 2.2 и 2.3, следует отметить еще одно полезное соотношение. Между силой роста и дисконтным множителем декурсивных процентов существует следующая связь:
(38)

По мере усложнения задач, стоящих перед финансовым менеджментом, сфера применения непрерывных процентов будет расширяться, так как при этом становится возможным использовать более мощный математический аппарат. Особенно наглядно это проявляется в случае непрерывных процентных ставок.
В самом деле, как для простых, так и для сложных процентов факт непрерывности их начисления ни у кого не вызывает сомнений (годовая ставка 36% означает 3% в месяц, 0,1% в день и т.д., то есть можно начислять проценты хоть за доли секунды). Но точно такой же аксиомой для финансов является признание возможности мгновенного реинвестирования любых полученных сумм. Что же мешает совместить два этих предположения? В теории сумма начисленных процентов может (и должна) реинвестироваться сразу по мере ее начисления, т.е. непрерывно. В данном утверждении ничуть не меньше логики, чем в предположении, что реинвестирование должно производиться дискретно. Почему реинвестирование 1 раз в год считается более "естественным" чем 12 или 6 раз? Почему эта периодичность привязывается к календарным периодам (год, квартал, месяц), почему нельзя реинвестировать начисленные сложные проценты, скажем 39 раз в год или 666 раз за период между двумя полнолуниями? На все эти вопросы ответ, скорее всего, будет один – так сложилось, так привычно, так удобнее. Но выше уже было отмечено, что практический расчет величины реальных денежных потоков(например, дивидендных или купонных выплат) и определение доходности финансовых операций это далеко не одно и то же. Если привычнее и удобнее выплачивать купон по облигации 2 раза в год, то так и следует поступать. Но, определять доходность этой операции более логично по ставке непрерывных процентов.

Таблица 2.3. Эквивалентность сложных процентных ставок

Пример:
по вкладу в размере 10 тыс. рублей начисляется 25 простых процентов в год. В конце 1 года вклад возрастет до 12500 рублей. Доходность, измеренная как по простой (формула 12), так и сложной (15) процентной ставке i, составит 25% годовых. Однако, измеряя доходность по номинальной ставке j (16) при m = 2, получим лишь 23,61%, т.к. в этом случае будет учтена потерянная вкладчиком возможность реинвестирования процентов хотя бы 2 раза в год. Если же измерить доходность по силе роста (19), то она окажется еще ниже – всего 22,31%, т.к. теоретически он мог реинвестировать начисленные проценты не 2 раза в год, а непрерывно.

2.3 Определение современной и будущей величины денежных потоков
В финансовом анализе для обозначения денежных потоков в наиболее общем смысле используется термин рента.
Каждый отдельный рентный платеж называют членом ренты .
Частным случаем ренты является финансовая рента или аннуитет – такой поток платежей, все члены которого равны друг другу, так же как и интервалы времени между ними. Часто аннуитетом называют финансовый актив, приносящий фиксированный доход ежегодно в течение ряда лет.
В буквальном переводе "аннуитет" подразумевает, что платежи происходят с интервалом в один год, однако встречаются потоки с иной периодичностью выплат.
Очевидно, что рента – это более широкое понятие, чем аннуитет, так как существует множество денежных потоков, члены которых не равны друг другу или распределены неравномерно.

Форму аннуитетов имеют многие финансовые потоки, например выплата доходов по облигациям или платежи по кредиту, страховые взносы и др. Можно сказать, что финансы тяготеют к упорядочению денежных потоков, так как равномерность любых процессов связана с их упорядоченностью, а следовательно – предсказуемостью и определенностью. И хотя риск как мера неопределенности постоянно присутствует в финансах, однако с увеличением этого риска происходит трансформация финансовой деятельности в индустрию азартных игр. Различие между двумя ценными бумагами (облигацией, имеющей высокий рейтинг, и лотерейным билетом) состоит именно в том, что первая из них с достаточно высокой вероятностью гарантирует ее владельцу возникновение упорядоченного положительного денежного потока (аннуитета ).
Принцип временной ценности денег делает невозможным прямое суммирование членов ренты. Для учета влияния фактора времени к каждому члену ренты применяются рассмотренные выше правила наращения и дисконтирования. Причем в анализе денежных потоков применяется техника вычисления только сложных процентов, то есть предполагается, что получатель потока имеет возможность реинвестировать получаемые им суммы.. Если бы размеры рент всегда ограничивались двумя-тремя членами, то необходимость создания специальных способов расчета денежных потоков, возможно, и не возникла. Ни в теории ни на практике таких ограничений нет, наоборот, существуют большие, очень большие и даже бесконечные денежные потоки (вечные ренты), поэтому были разработаны специальные методы, позволяющие анализировать ренту не по каждому ее члену в отдельности, а как единую совокупность – рассчитывать ее будущую и приведенную величины, а также определять размеры других важных параметров ренты.

В процессе начисления сложных процентов на единичную сумму Р возникает геометрическая прогрессия со знаменателем наращенная сумма S представляет собой последний член этой прогрессии
Денежный поток представляет собой совокупность таких единичных сумм поэтому наращение денежного потока означает нахождение суммы всех k последних членов геометрических прогрессий, возникающих по каждому из них. В случае аннуитета задача упрощается, т.к. в этом случае будет постоянной величиной = Р. То есть возникает одна геометрическая прогрессия с первым членом Р и знаменателем . Отличие от сложных процентов для единичного платежа здесь заключается в том, что требуется найти не последний член прогрессии, а ее сумму. В случае дисконтирования аннуитета меняется лишь знаменатель прогрессии – он будет равен не , а .
Приведенная стоимость аннуитета находится как сумма вновь полученной геометрической прогрессии.

Наряду с членом ренты (обозначим его R) любой денежный поток характеризуется рядом других параметров:
период ренты (t) - временной интервал между двумя смежными платежами;
срок ренты (n) - общее время, в течение которого она выплачивается;
процентная ставка (i) - ставка сложного процента, используемая для наращения и дисконтирования платежей, из которых состоит рента;
число платежей ха 1 период ренты (P) - используется в том случае, если в течение 1 периода ренты, производится больше, чем 1 выплата денежных средств;
число начислений процентов в течение 1 периода ренты (m) - при начислении (дисконтировании) по номинальной процентной ставке (j).

В зависимости от числа платежей за период различают годовые и p-срочные ренты:
в первом случае за 1 период ренты (равный, как правило 1 году) производится 1 выплата ;
во втором, в течение периода производится p выплат .
В случае очень частых выплат, рента может рассматриваться как непрерывная .
значительно чаще в финансовом анализе имеют дело с дискретными рентами, для которых Р - конечное целое число.
Так же как и при использовании сложной процентной ставки для единичных сумм, наращение (дисконтирование) рент может производиться 1 раз за период, m раз за период или непрерывно.

По величине членов денежного потока ренты могут быть постоянными (с равными членами) и переменными.
По вероятности выплат ренты делятся на верные и условные. В случае условной ренты выплата ее членов ставится в зависимость от наступления какого-либо условия.
По своей общей продолжительности (или по числу членов) различают ограниченные (с конечным числом членов) и бесконечные (вечные, бессрочные) ренты.
По отношению к фиксированному моменту начала выплат ренты могут быть немедленными и отложенными (отсроченными).
Ренты, платежи по которым производятся в конце периода называются обычными или постнумерандо ; при выплатах в начале периода говорят о рентах пренумерандо.

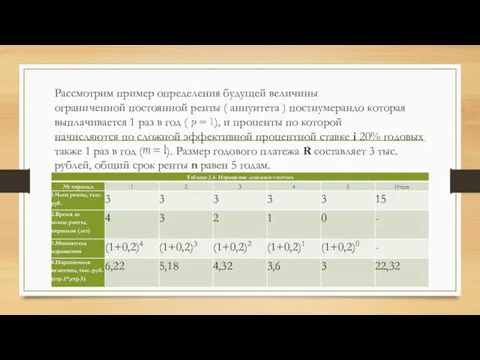
Рассмотрим пример определения будущей величины ограниченной постоянной ренты ( аннуитета ) постнумерандо которая выплачивается 1 раз в год ( ), и проценты по которой начисляются по сложной эффективной процентной ставке i 20% годовых также 1 раз в год ( ). Размер годового платежа R составляет 3 тыс. рублей, общий срок ренты n равен 5 годам.

Полученное значение (22,32 тыс. руб.) заметно больше арифметической суммы отдельных членов ренты (15 тыс. руб.), однако она значительно меньше той гипотетической суммы, которая могла быть получена, если бы мы захотели нарастить по ставке 20% все 15 тыс. руб. за весь срок ренты (15*; 1,25). Наращенная сумма ренты S получена путем последовательного начисления процентов по каждому члену ренты и последующего суммирования полученных результатов. Введя обозначение k = номеру периода ренты, в наиболее общей форме данный процесс можно выразить следующей формулой:
(1)

В нашем примере член ренты R неизменен в течение всего срока, процентная ставка i также постоянна. Поэтому наращенную величину ренты можно найти как сумму геометрической прогрессии с первым членом 3000 и знаменателем (1+0,2).
Следовательно, от общей формулы наращения ренты (1) можно перейти к ее частному случаю – формуле наращения аннуитета:
(2)
Второй сомножитель этого выражения – называется множителем наращения аннуитета. Так же как и в случае с начислением процентов на единичные суммы, значения таких множителей табулированы, что позволяет облегчить процентные вычисления денежных потоков.

Наращение денежных потоков имеет место при периодическом внесении на банковский депозит фиксированных сумм с целью накопления финансового фонда к определенному моменту времени. Например, разместив долгосрочный облигационный заем, предприятие готовится к погашению суммы основного долга в конце срока займа путем периодического внесения на банковский счет фиксированных платежей под установленный процент. Таким образом к моменту погашения облигационного займа у предприятия накопятся достаточные средства в этом фонде. Аналогичные задачи решаются в ходе формирования пенсионного фонда или при накоплении суммы для оплаты обучения детей. Например, заботясь о своей старости, человек может наряду с обязательными отчислениями в государственный Пенсионный фонд, вносить часть своего ежемесячного заработка на банковский депозит под проценты. Наращение суммы такого вклада будет происходить по описанному выше алгоритму. Таким же путем предприятия могут формировать амортизационный фонд для плановой замены оборудования.

Обратный по отношению к наращению процесс – дисконтирование денежного потока имеет еще большую важность для финансового менеджмента, так как в результате определяются показатели, являющиеся в настоящее время основными критериями принятия финансовых решений. Рассмотрим этот процесс более подробно. Предположим, что рассмотренный в нашем примере денежный поток характеризует планируемые поступления от реализации инвестиционного проекта. Доходы должны поступать в конце периода. Так как эти поступления планируется получить в будущем, а инвестиции, необходимые для выполнения проекта, должны быть произведены уже сегодня, предприятию необходимо сопоставить величину будущих доходов с современной величиной затрат. Как уже было сказано выше, использование для сравнения арифметической суммы членов потока (15 тыс. руб.) бессмысленно, так как эта сумма не учитывает влияние фактора времени. Для обеспечения сопоставимости данных величина будущих поступлений должна быть приведена к настоящему моменту, иными словами данный денежный поток должен быть дисконтирован по ставке 20%. Предприятие сможет определить сегодняшнюю стоимость будущих доходов. 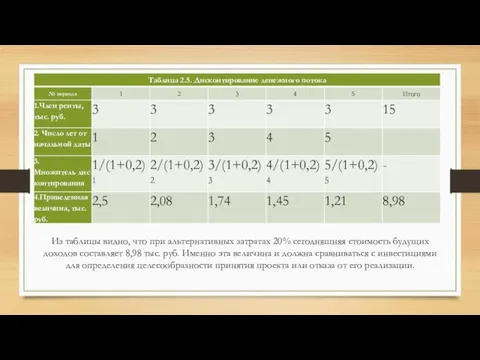При этом процентная ставка будет выступать в качестве измерителя альтернативной стоимости этих доходов: она показывает, сколько денег могло бы получить предприятие, если бы разместило приведенную (сегодняшнюю) стоимость будущих поступлений на банковский депозит под 20%.

Дисконтирование денежного потока предполагает дисконтирование каждого его отдельного члена с последующим суммированием полученных результатов. Для этого используется дисконтный множитель математического дисконтирования по сложной учетной ставке i . Операции наращения и дисконтирования денежных потоков взаимообратимы, то есть наращенная сумма ренты может быть получена начислением процентов по соответственной сложной ставке i на современную (приведенную) величину этой же ренты

Из таблицы видно, что при альтернативных затратах 20% сегодняшняя стоимость будущих доходов составляет 8,98 тыс. руб. Именно эта величина и должна сравниваться с инвестициями для определения целесообразности принятия проекта или отказа от его реализации.

Обобщая алгоритм, по которому выполнялись расчеты, получаем общую формулу дисконтирования денежных потоков:
(3)
Так как в нашем примере и постоянные величины, то снова применяя правило суммирования геометрической прогрессии, получим частную формулу дисконтирования аннуитета:
(4)
Второй сомножитель этого выражения – – называется дисконтным множителем аннуитета.

Формулы (3) и (4) описывают наиболее общие случаи наращения и дисконтирования аннуитетов: рассматриваются только ограниченные ренты, выплаты и начисление процентов производятся 1 раз в году, используется только эффективная процентная ставка . Так же как и в случае единичных сумм все эти параметры могут меняться. Поэтому существуют модифицированные формулы наращения и дисконтирования аннуитетов, учитывающие особенности отдельных денежных потоков. Основные из них, относящиеся к ограниченным денежным потокам, представлены в табл. 2.6

Таблица 2.6. Основные формулы наращения и дисконтирования ограниченных аннуитетов

В табл. 2.6 не нашли отражения формулы расчета неограниченных денежных потоков, т.е. вечных рент или перпетуитетов. Существуют финансовые инструменты, предполагающие бессрочную выплату доходов их держателям. Одним из примеров таких ценных бумаг являются т.н. консоли (консолидированные ренты), эмитируемые британским казначейством начиная с XVIII века. В случае смерти владельца они передаются по наследству, обеспечивая тем самым действительную "бесконечность" денежного потока. Очевидно, что будущую стоимость ренты такого рода определить невозможно – ее сумма также будет стремиться к бесконечности, однако приведенная величина вечного денежного потока может быть выражена действительным числом. Причем, формула ее определения очень проста: (17)
где R – член ренты (разовый платеж),
i – сложная процентная ставка.

Например, по условиям страхового договора компания обязуется выплачивать 5 тыс. рублей в год на протяжении неограниченного периода, т.е. вечно. Чему должна быть равна стоимость этого перпетуитета, если уровень процентной ставки составит 25% годовых? В соответствии с (17) текущая стоимость всех предстоящих платежей по договору будет равна 20 тыс. рублей (5 / 0,25).
Если неограниченная рента выплачивается раз в году, и начисление процентов по ней производится раз за год, причем ,
то формула расчета ее приведенной стоимости принимает вид:
(18)
где j – номинальная процентная ставка.

Предположим, рассмотренный выше перпетуитет будет выплачиваться дважды в год по 2,5 тыс. рублей, столько же раз будут начисляться проценты (25% в этих условиях становится номинальной ставкой). Его стоимость останется неизменной 20 тыс. рублей ((2,5 + 2,5) / 0,25).
В наиболее общем виде формула приведенной стоимости перпетуитета записывается следующим образом:
(19)
В принципе, ее можно использовать во всех случаях, подставляя соответствующие значения параметров или i . Если предположить четырехразовое начисление процентов по рассматриваемому перпетуитету, то в соответствии с (19) его текущая стоимость составит:

Интересно отметить связь существующую между годовой вечной и годовой ограниченной рентами ( аннуитетами ). Преобразовав правую часть формулы (4), получим:
(20)
То есть современная величина конечной ренты, имеющей срок n периодов, может быть представлена как разница между современными величинами двух вечных рент, выплаты по одной из которых начинаются с первого периода, а по второй – с периода ( ) . В случае, если член вечной ренты R ежегодно увеличивается с постоянным темпом прироста q , то приведенная стоимость такой ренты определяется по формуле: (21)
где R1 – член ренты в 1-м году.

Данная формула имеет смысл при . Она применяется в оценке обыкновенных акций. При сравнении приведенной стоимости различных аннуитетов можно избежать громоздких вычислений, запомнив следующее правило: увеличение числа выплат по ренте в течение года (P) увеличивает ее текущую стоимость, увеличение числа начислений процентов (m), наоборот, уменьшает. При заданных значениях наиболее высокий результат даст дисконтирование p-срочной ренты с 1 начислением процентов в год ( ). Самый низкий результат при этих же условиях будет получен по годовой ренте ( )
с непрерывным начислением процентов. По мере увеличения P современная величина ренты будет расти, по мере роста m она будет снижаться. Причем изменение P дает относительно больший результат, чем изменение m .

То есть любая p-срочная рента даже с непрерывным начислением процентов
( ) будет стоить дороже, чем годовая рента ( ) с 1 начислением процентов в год ( ) . Например, по облигации предусмотрена ежегодная выплата 1 тыс. рублей в течение 5 лет. Процентная ставка составляет 20%. При начислении декурсивных процентов 1 раз в год стоимость этой ренты по базовой формуле(4) составит 2,99 тыс. рублей. Если выплаты будут производиться 2 раза в год по 500 рублей, то по формуле (12) стоимость ренты будет равна уже 3,13 тыс. рублей. Но если по последнему варианту начислять проценты 2 раза в год (13), текущая величина ренты снизится до 3,07 тыс. рублей. Если же двукратное начисление применить к исходному варианту при (11), то приведенная стоимость ренты станет еще меньше 2,93 тыс. рублей. Самым дешевым будет вариант годовой ренты ( ) с непрерывным начислением процентов (15) – 2,86 тыс. рублей.

2.4 Вычисление основных параметров денежных потоков
Несмотря на то, что общее количество формул, приведенных в трех предыдущих лекциях, уже приблизилось к сотне, можно смело утверждать, что это лишь малая часть того, что имеется в арсенале финансовых вычислений. Буквально по каждому из рассмотренных способов осталась масса незатронутых вопросов: ренты пренумерандо, переменные денежные потоки, использование простых процентов в анализе рент и так далее почти до бесконечности. Тем не менее, усвоив базовые понятия финансовых расчетов, можно заметить, что все дальнейшие рассуждения строятся по довольно универсальному алгоритму. Определяется математическая природа понятия и основные ограничения, накладываемые на него при практическом использовании.

Например, сложные проценты наращиваются в геометрической прогрессии. Они применяются по большей части в расчетах по долгосрочным финансовым операциям. Затем находится решение основных задач, связанных с данным понятием – начисление и дисконтирование по сложным процентным и учетным ставкам. После этого разрабатывается методика расчета остальных параметров уравнений, описывающих данное понятие, и решается проблема нахождения эквивалентных значений отдельных параметров. При этом основным методом решения задач является преобразование или приравнивание друг к другу множителей наращения ( дисконтирования ) различных показателей. Поняв эти закономерности, можно отказаться от заучивания всех возможных формул и попытаться применить данную методику для решения конкретных финансовых задач, держа при этом в памяти лишь полтора-два десятка основополагающих выражений (например, формулы расчета декурсивных и антисипативных процентов и т.п.).

Используем данный алгоритм для финансового анализа денежных потоков, в частности, для расчета отдельных параметров финансовых рент. Например, предприятию через три года предстоит погасить задолженность по облигационному займу в сумме 10 млн. рублей. Для этого оно формирует погасительный фонд путем ежемесячного размещения денежных средств на банковский депозит под 15% годовых сложных процентов с начислением 1 раз в год. Чему должна быть равна величина одного взноса на депозит, чтобы к концу третьего года в погасительном фонде вместе с начисленными процентами накопилось 10 млн. рублей?
Планируемые предприятием взносы представляют собой трехлетнюю p-срочную ренту, , , будущая стоимость которой должна быть равна 10 млн. рублей. Неизвестным является ее единственный параметр – член ренты R.
В качестве базовой используем формулу (6) из табл. 2.6

Данное уравнение следует решить относительно так как планируются ежемесячные взносы) обозначим . Преобразовав базовую формулу, получим
То есть, размер ежемесячного взноса должен составить примерно 225 тыс. рублей (более точная цифра 224,908).
Размер долга по займу (10 млн. рублей) был задан как условие предыдущего примера. На самом деле, часто данный параметр также является вычисляемой величиной, т.к. наряду с основной суммой займа должник обязан выплачивать проценты по нему.

Предположим, что 10 млн. рублей – это основная задолженность по облигационному займу, кроме этого необходимо ежегодно выплачивать кредиторам 10% основной суммы в виде процентов. Чему будет равна сумма ежемесячного взноса в погасительный фонд с учетом процентных выплат по займу? Так как проценты должны выплачиваться ежегодно и их годовая сумма составит 1 млн. рублей (10 млн. рублей * 10%), нам опять следует рассчитать член ренты по ренте сроком
По базовой формуле (6) его величина составит:
Ежемесячно в погасительный фонд будет необходимо вносить около 78 тыс. рублей (более точная цифра 78,0992) для ежегодной выплаты процентов в сумме 1 млн. рублей. Таким образом общая сумма ежемесячных взносов в погасительный фонд составит 303 тыс. рублей (225 + 78).

Условиями займа может быть предусмотрено присоединение суммы начисленных за год процентов к основному долгу и погашение в конце срока наращенной величины займа. То есть в конце срока эмитенту займа придется возвратить 13 млн. 310 тыс. рублей (10 * (1 + 0,1)3). Величину ежемесячного взноса в погасительный фонд найдем, используя все ту же базисную формулу (6):
То есть ежемесячно необходимо вносить на банковский депозит около 300 тыс. рублей более точно – 299,35).

Аналогичный подход может быть применен к формированию амортизационного фонда. Известно, что амортизация основных фондов – важнейшая составная часть чистого денежного потока предприятия, остающаяся в его распоряжении. В каждом рубле получаемой предприятием выручки содержится доля амортизационных отчислений. Поэтому нет ничего противоестественного в том, чтобы предприятие, "расщепляя" поступающую выручку, перечисляло на банковский депозит сумму амортизации по каждому платежу от покупателя. В этом случае накопление амортизационного фонда происходило бы значительно быстрее за счет начисления процентов.

Предположим, что по основным фондам первоначальной стоимостью 50 млн. рублей предприятие начисляет амортизацию по годовой ставке 12,5% (линейный метод). Срок службы оборудования 8 лет. Ежегодно начисляется 6,25 млн. рублей амортизационных отчислений. Но если предприятие располагает возможностью размещения денежных средств хотя бы под 10% годовых, то для накопления 50 млн. рублей в течение 8 лет ему понадобится ежегодно размещать на депозите лишь по 4, 37 млн. рублей: преобразовав формулу (2) из предыдущей лекции, получим:

Если же взносы на депозит производить ежемесячно ( ), то, снова применяя формулу (6), и деля полученный результат на 12, найдем:
Ежемесячный взнос на депозит должен составить около 350 тыс. рублей (более точно – 348,65). При этом ежемесячные амортизационные отчисления по линейному методу составят 520,8 тыс. рублей (6,25 / 12). Задачу можно сформулировать иначе: за сколько лет предприятие возместит первоначальную стоимость основных средств, размещая на депозите сумму амортизационных отчислений по линейному методу (520,8 тыс. рублей в месяц или 6,25 млн. рублей в год).

Для решения этой задачи (нахождение срока ренты n ) снова понадобится формула (6), но теперь она будет преобразована следующим образом:
Полученное дробное число лет в соответствии с правилами выполнения финансовых расчетов должно быть округлено до ближайшего целого. Однако, при
, округляется произведение в нашем случае оно составляет 71,52 (5,96 * 12). Округлив его до 71 и разделив на 12, получим
При любых способах округления, полученное значение на 2 года меньше, чем срок амортизации основных фондов по линейному методу. То есть предприятие таким способом может накопить сумму для замены изношенного оборудования на 2 года быстрее.

Необходимость выплачивать проценты кредитору на остаток банковской ссуды или коммерческого кредита ставит перед предприятиями задачу разработки оптимального плана погашения долга. Дело в том, что оставляя неизменной сумму основной задолженности в течение всего срока займа, предприятие будет вынуждено выплатить максимально возможную сумму процентов поэтому займу. Если же оно периодически будет направлять часть средств на погашение основного долга, то сможет сэкономить на процентах, которые начисляются на остаток задолженности. Возможны различные стратегии амортизации займов. Например, предприятие может периодически уплачивать фиксированную сумму в погашение основной задолженности. Тогда в каждом новом периоде ему понадобится меньше денег на оплату процентов, то есть общие расходы по обслуживанию долга за период (срочная уплата) будут снижаться.

Погашая ежегодно 2 млн. рублей из общей суммы 3-летнего займа 6 млн. рублей, выданного под 20 процента годовых, предприятие в 1-й год выплатит 1200 тыс. рублей процентов (6000 * 0,2). Срочная уплата за этот период составит 3200 тыс. рублей (2000 + 1200). За второй год проценты составят уже 800 тыс. рублей (4000 * 0,2), срочная уплата – 2800 тыс. рублей (2000 + 800) и т.д. Сумма выплачиваемых процентов будет снижаться в арифметической прогрессии с первым членом 1200 тыс. рублей (p*i) и разностью -400 тыс. рублей (-p * i / n), n означает число членов прогрессии, в данном примере оно равно 3. Сумма этой прогрессии будет равна 2400 тыс. рублей (3 * 1200 – 2 * 3 * 400 / 2), а это значительно меньше суммы процентов, которую пришлось бы уплатить предприятию в случае единовременного погашения основного долга в конце срока ссуды – 4368тыс. рублей (6000 * (1 + 0,2)3 - 6000).

Возможен другой вариант, когда величина срочной уплаты на протяжении всего срока займа остается неизменной, но постепенно меняется ее структура – уменьшается доля, идущая на погашение процентов и увеличивается доля, направляемая в уплату по основному долгу. В этом случае сначала необходимо определить размер срочной уплаты, которая рассчитывается как величина члена ренты, текущая стоимость которой равна первоначальной сумме долга при дисконтировании по процентной ставке, установленной по займу. Преобразовав формулу приведения аннуитета (4) из предыдущей лекции, найдем значение R:
Для полного погашения задолженности по ссуде понадобится произвести 3 погасительных платежа по 2848 тыс. рублей каждый. Не вдаваясь в подробности расчета структуры срочной уплаты по каждому году, отметим, что в сумме предприятию придется заплатить по займу 8544 тыс. рублей, т.е. общая сумма процентов составит 2544 тыс. рублей (8544 – 6000), что заметно выше, чем по первому варианту.

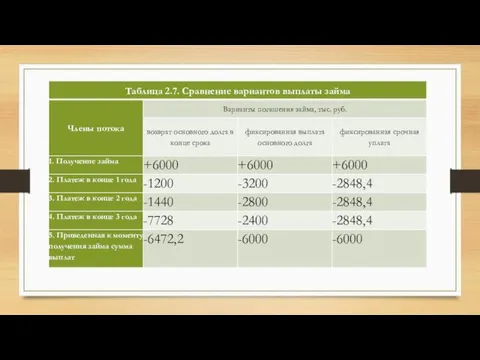
Сопоставление различных вариантов погашения займа только по критерию общей величины выплаченных процентов, не вполне корректно – сравниваются различные денежные потоки, для которых кроме абсолютных сумм имеет значение, в каком конкретно периоде времени деньги были уплачены или получены. Рассмотрим подробнее, что из себя представляет каждый из этих потоков (табл. 2.7). Вследствие действия принципа временной ценности денег сложение членов этих потоков является бессмысленной операцией – платежи, производимые с интервалом 1 год, несопоставимы. Поэтому в стр. 5 табл. 2.7 рассчитана дисконтированная поставке 20% величина каждого из потоков. Так как в последней графе этой таблицы представлен аннуитет, то его расчет произведен по формуле (4) из предыдущего пар аграфа. Два остальных потока состоят из неравных членов, их дисконтирование произведено по общей формуле (3).

Как видно из результатов расчетов, наибольшую отрицательную величину (-6472,2) имеет приведенная сумма платежей по первому потоку, она даже превышает сумму полученного займа. То есть, погашая долг на таких условиях, предприятие реально несет финансовые потери. Два последних варианта не ухудшают финансового положения предприятия.

Сравнивая между собой приведенные величины денежных притоков и оттоков по финансовой операции, определяют важнейший финансовый показатель чистая приведенная стоимость (NPV – от английского net present value). Наиболее общая формула определения этого показателя:
(1)
где Io – первоначальные инвестиции в проект (оттоки денег),
PV – приведенная стоимость будущих денежных потоков по проекту.
При использовании этой формулы все денежные притоки (доходы) обозначаются положительными цифрами, оттоки денежных средств (инвестиции, затраты) – отрицательными. В нашем примере первоначально предприятие получало приток денежных средств (сумма займа 6 млн. рублей), а затем в течение 3 лет производило денежные расходы, т.е. оттоки средств. Поэтому к первоначальному моменту приводились не поступления, а затраты.

Обычно при реализации инвестиционных проектов наблюдается обратная картина: сначала предприятие вкладывает средства, а затем получает периодические доходы от этих вложений. Поэтому, преобразуя (1) с учетом правил дисконтирования денежных потоков(формула (4) из предыдущей лекции), получаем:
(2)
где n – общий срок финансовой операции (проекта),
Rk – элемент дисконтируемого денежного потока ( член ренты ) в периоде k,
k – номер периода.

Под процентной ставкой i (в данном случае ее называют ставкой сравнения) понимается годовая сложная эффективная ставка декурсивных процентов. Срок операции n в общем случае измеряется в годах. Если же реальная операция не отвечает этим условиям, т.е. интервалы между платежами не равны году, то в качестве единицы измерения срока принимаются доли года, измеренные как правило в месяцах, деленных на 12. Например, инвестиции в сумме 500 тыс. рублей принесут в первый месяц 200 тыс. рублей дополнительного дохода, во второй 300 тыс. рублей и в третий – 700 тыс. рублей. Ставка сравнения равна 25%. Чистая приведенная стоимость данного проекта составит 1 млн. 147 тыс. руб.:

Довольно распространенной является ошибка, когда в подобных случаях пытаются рассчитать месячную процентную ставку делением годовой ставки на 12, а срок проекта измеряют в целых месяцах (вместо 1 / 12 года берут 1 месяц вместо 2 / 12 – 2 и т.д.). В этом случае будет получен неправильный результат, т.к. возникнет эффект ежемесячного реинвестирования начисляемых сложных процентов. Чтобы получить эквивалентный результат, для нахождения месячной ставки необходимо предварительно пересчитать годовую эффективную ставку i в номинальную j
при по формуле
(см. гл. 2.2) . В данном случае эквивалентной является номинальная годовая ставка 22,52% ставка, разделив которую на 12 можно получить значение для помесячного дисконтирования денежного потока.

Если денежный поток состоит из одинаковых и равномерно распределенных выплат (то есть представляет собой аннуитет), можно упростить расчет NPV,
воспользовавшись формулами дисконтирования аннуитетов из табл. 2.6 предыдущего параграфа. Например, если бы в рассматриваемом проекте было предусмотрено получение в течение трех месяцев по 400 тыс. рублей дохода ежемесячно (то есть ), то следовало рассчитать приведенную стоимость аннуитета сроком 3 / 12 года и числом выплат .
Применив формулу (12) из предыдущего параграфа, получим

Кроме правильного вычисления чистой приведенной стоимости, необходимо понимать ее финансовый смысл. Положительное значение этого показателя указывает на финансовую целесообразность осуществления операции или реализации проекта. Отрицательная NPV свидетельствует об убыточности инвестирования капитала таким образом. В примере с проектом получено очень хорошее значение NPV, свидетельствующее о его инвестиционной привлекательности. Возвратившись к данным табл. 2.7, можно видеть, что два последних варианта погашения долга дают нулевую NPV, то есть в финансовом плане само по себе пользование заемными средствами не принесет предприятию ни вреда ни пользы. Если же оно изберет первый вариант (возврат основной суммы долга по окончании его срока), то получит отрицательную NPV –472,2 тыс. рублей, следовательно такой план погашения задолженности принесет ему финансовые потери.

О достоинствах и особенностях чистой приведенной стоимости будет очень подробно говориться в последующих лекциях. Остается только заметить, что значение ее для финансового менеджмента настолько высоко, что многократно окупает затраты труда по изучению и осмыслению всех вышеприведенных формул финансовых вычислений. Вторым столь же важным финансовым показателем является внутренняя норма доходности (IRR – от английского internal rate of return). Рассмотрим еще один инвестиционный проект. Внедрение новой технологии требует единовременных затрат в сумме 1,2 млн. рублей. Затем в течение 4 лет предприятие планирует получать дополнительный денежный поток от этих инвестиций в размере: 1-й год – 280 тыс. рублей, 2-й год – 750 тыс. рублей, 3-й год – 1 млн. рублей и 4-й год – 800 тыс. рублей. Рассчитаем NPV этого проекта при ставке сравнения 30% годовых:

Реализация проекта может принести предприятию 194,4 тыс. рублей чистой приведенной стоимости при условии использования ставки сравнения 30%. А при какой процентной ставке проект будет иметь нулевую NPV, то есть, какой уровень доходности приравняет дисконтированную величину денежных притоков к сумме первоначальных инвестиций? Взглянув на формулу расчета NPV, можно сделать вывод, что увеличение ставки I снижает величину каждого члена потока и общую их сумму, следовательно, чем больше будет уровень ставки, приравнивающей NPV к нулю, тем более мощным будет сам положительный денежный поток. Иными словами, мы получаем характеристику финансовой эффективности проекта, которая как бы заложена внутри него самого. Поэтому данный параметр и получил название внутренняя норма доходности (иногда используется термин внутренняя норма рентабельности, внутренняя процентная ставка и др.). Итак IRR это такая годовая процентная ставка, которая приравнивает текущую стоимость денежных притоков по проекту к величине инвестиций, т.е. делает NPV проекта равным нулю.