Содержание
- 2. №1. Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и
- 3. №1. Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и
- 4. №2. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми 70
- 5. №3. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на
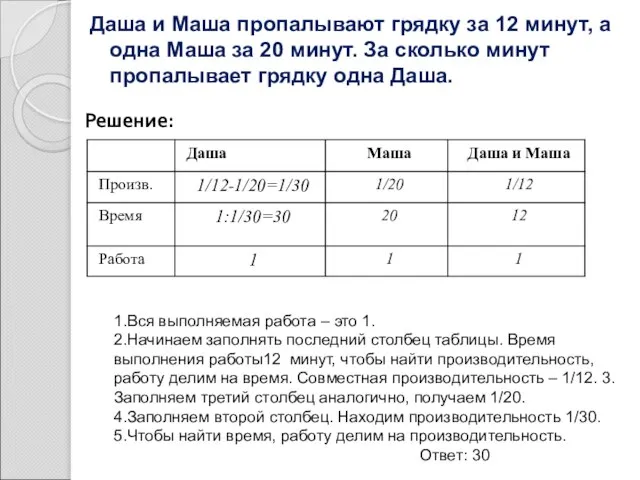
- 6. Даша и Маша пропалывают грядку за 12 минут, а одна Маша за 20 минут. За сколько
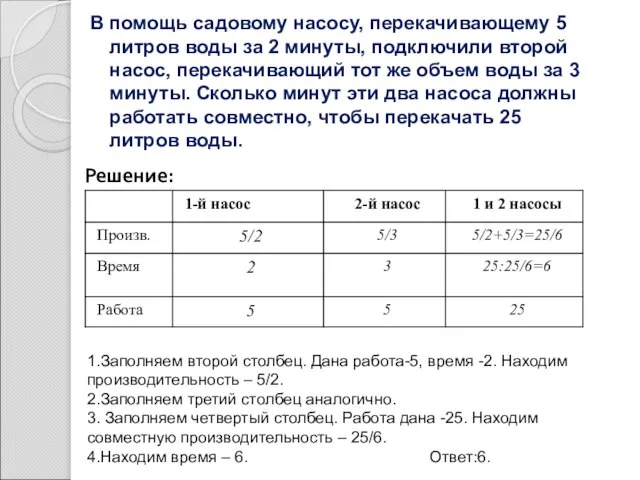
- 7. В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот
- 8. С1. Решите систему уравнений 1. ОДЗ: 2. Помним, что 3. Из второго уравнения получаем: или 4.
- 9. В задачах С1 особое внимание уделить области допустимых значений. Т.е. это задание предполагает «отсев» посторонних корней
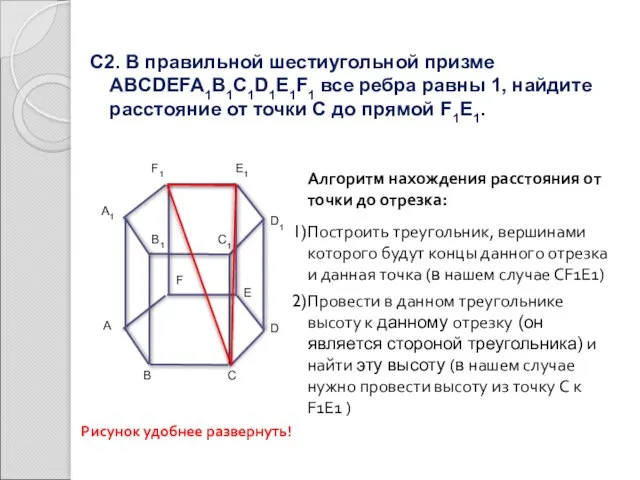
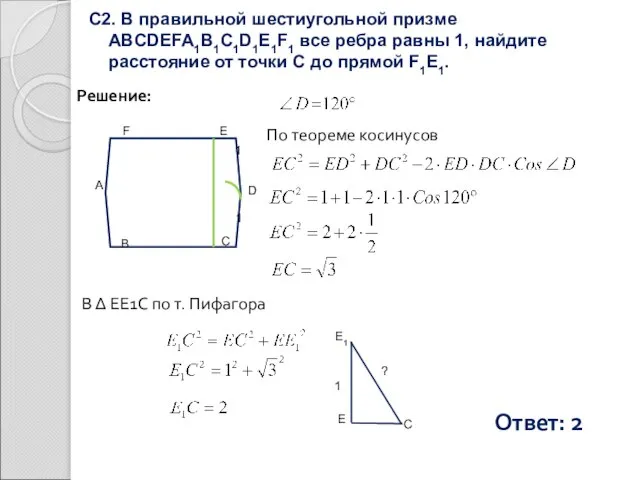
- 10. С2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1, найдите расстояние от точки С до
- 11. С2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1, найдите расстояние от точки С до
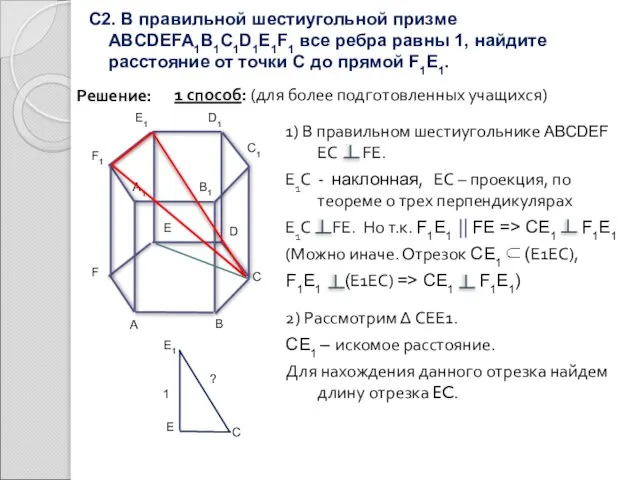
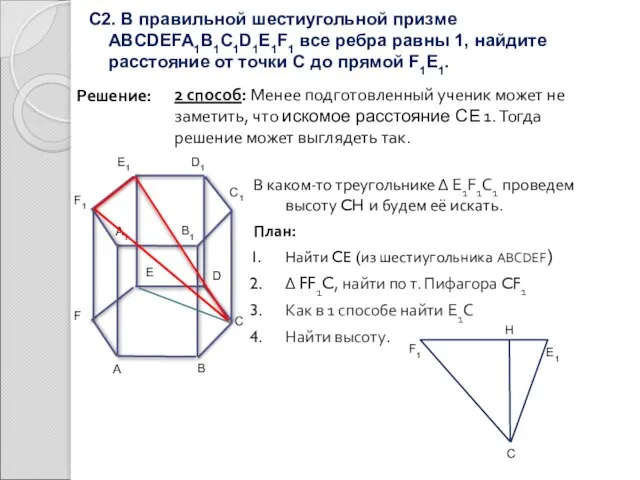
- 12. С2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1, найдите расстояние от точки С до
- 13. С2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1, найдите расстояние от точки С до
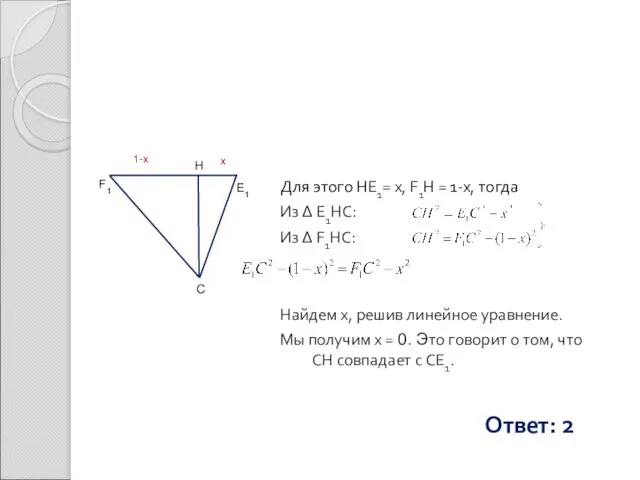
- 14. Для этого HE1= x, F1H = 1-x, тогда Из Δ E1HC: Из Δ F1HC: Найдем х,
- 15. С3. Решить неравенство. (Из сборника «Математика. Подготовка к ЕГЭ» под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова) Решение:
- 16. С3. Решить неравенство. (Из сборника «Математика подготовки к ЕГЭ» под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова) Решение:
- 18. Скачать презентацию








 Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Информационное оснащение женских консультаций
Информационное оснащение женских консультаций Презентация на тему Сложение чисел с помощью координатной прямой
Презентация на тему Сложение чисел с помощью координатной прямой  Что такое натуральные ткани? каковы их свойства?
Что такое натуральные ткани? каковы их свойства? Неорганические кислоты
Неорганические кислоты Фторхинолоны клиническая фармакология иособенности действия
Фторхинолоны клиническая фармакология иособенности действия ИГРА С БУДУЩИМ
ИГРА С БУДУЩИМ Антонио Гауди - великий архитектор
Антонио Гауди - великий архитектор Сообщающиеся сосуды
Сообщающиеся сосуды Плавание тел
Плавание тел Любимые места отдыха
Любимые места отдыха Повседневная жизнь земледельцев и горожан в средние века
Повседневная жизнь земледельцев и горожан в средние века Сводный медиаплан рекламной кампании
Сводный медиаплан рекламной кампании Лагерь молодёжного актива
Лагерь молодёжного актива Повесть Н.С.Лескова «Очарованный странник»
Повесть Н.С.Лескова «Очарованный странник» Мельник М.В. Управление риском
Мельник М.В. Управление риском Ошибки вокруг нас
Ошибки вокруг нас Приблизительные размеры территорий
Приблизительные размеры территорий Chanel SS21. Alberta Ferretti SS21. Вдохновение
Chanel SS21. Alberta Ferretti SS21. Вдохновение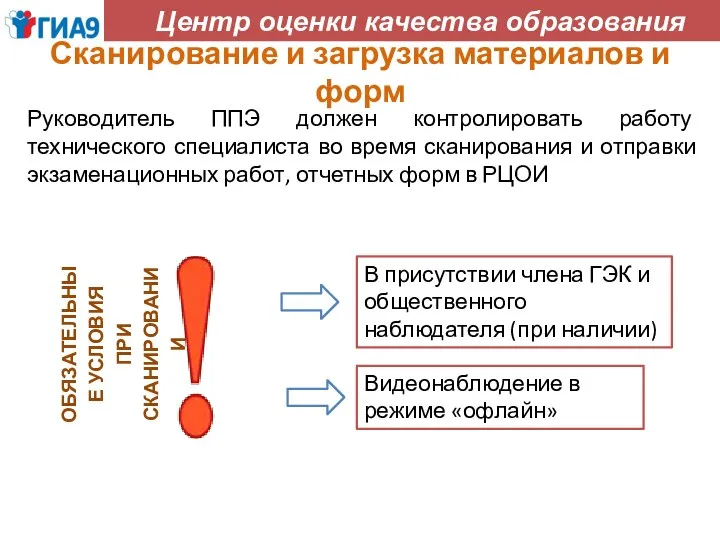 Обязательные условия при сканировании
Обязательные условия при сканировании chekhov
chekhov Презентация на тему Происхождение рас
Презентация на тему Происхождение рас  Обзор Информационно-аналитической системы «Семантический архив» 3.0
Обзор Информационно-аналитической системы «Семантический архив» 3.0 ГАЗЕТАК ПРАЗДНИКУ «ДЕНЬ МАТЕРИ»
ГАЗЕТАК ПРАЗДНИКУ «ДЕНЬ МАТЕРИ» Презентация на тему Памятник русскому солдату в Болгарии
Презентация на тему Памятник русскому солдату в Болгарии Как маркетинговая аналитика увеличивает продажи. Часть 1
Как маркетинговая аналитика увеличивает продажи. Часть 1 აუდიტი გამა
აუდიტი გამა Изделия из бересты
Изделия из бересты