vTmrDKBu4qamut0wl2py0w

Кусочно-заданная функция — функция, заданная несколькими формулами, в зависимости от значений аргумента, например:
y=

Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками. Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями. Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.

Рассмотрим кусочно-заданную функцию
y=

Создание графиков в программе Exel
Любые функции можно оформлять в виде графиков в Exel.
Данную кусочно-заданную функцию нужно прописывать через условие ЕСЛИ.
ОБЯЗАТЕЛЬНО нужно учитывать все ОДЗ функций для грамотного оформления графика.
Удобно следовать блок-схеме при написании условия

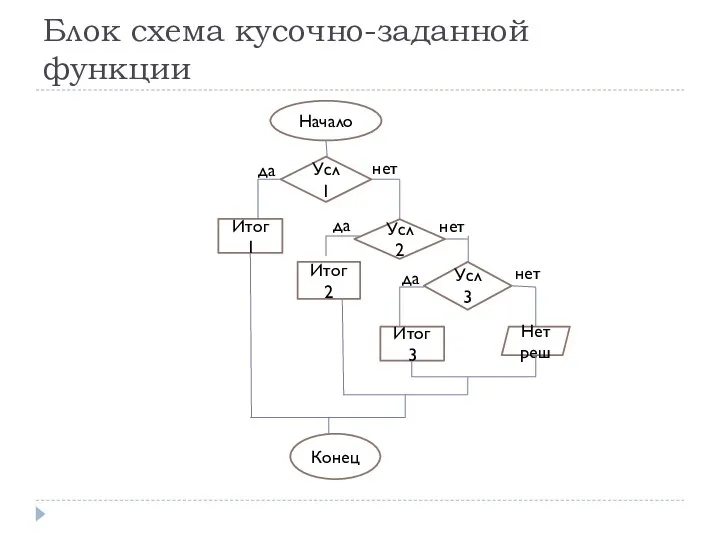
Блок схема кусочно-заданной функции
Начало
Усл 1
Итог 1
Усл 2
Усл 3
Итог 2
Нет реш
Итог 3
Конец
да
нет
да
нет
да
нет

Создание графика кусочно-заданной функции в Exel
Кусочно-заданная функция строится с помощью команды ЕСЛИ
1. Создаем значения x с необходимым нам шагом( возьмем от-10 до 10,шаг 1)
2. Записываем необходимые нам данные для построения(значения постоянных,x при которых не существует функция)
3. Далее в ячейке значения функции y вызываем команду ЕСЛИ
Значения,являющиеся постоянными(например a=5),следует «замораживать» кнопкой F4

Работа с командой ЕСЛИ
Общий вид функции =ЕСЛИ(логическое выражение, [значение если ИСТИНА], [значение если ЛОЖЬ])
В логическом выражении можно применять операторы сравнения:
> больше
< меньше
>= больше или равно
<= меньше или равно
= равно
<> не равно
Удобно использовать блок-схему при прописывании условий функции

Прописанное Условие для нашей функции
=ЕСЛИ(И(B4<3;SIN(B4)>0);КОРЕНЬ(SIN(B4));ЕСЛИ(И(B4>-3;B4<3;B4<>1;B4<>-1);10/((B4*B4)-5);ЕСЛИ(B4>4;B4*B4*B4;"net")))
Красный-условие первой функции
Зеленый – условие второй функции
Синий – условие третьей функции
Фиолетовый – условие,если ни одна функция не выполняется

Создание графика по данным функции
Выделяем область значений и определений функции,в которых она существует
Вставка->Точечный график
Далее открываем контекстное меню, нажав правой кнопкой на графике, и выбираем «Выбрать данные»
В открывшемся окне нажимаем кнопку «добавить» и добавляем допустимые значения X и Y в соответствующие строки