Содержание
- 2. В медицине и здравоохранении часто используются, сознательно или неосознанно, различные статистические концепции при принятии решений по
- 3. Статистика!!! …..НУ И ЧТО?
- 4. СТАТИСТИКА - это инструмент для анализа экспериментальных данных и результатов популяционных исследований; - это язык с
- 5. СТАТИСТИКА Наука, изучающая количественные закономерности материальных явлений в неразрывной связи с их качественной стороной. Точная наука,
- 6. БИОСТАТИСТИКА приложение общей теории статистики для решения научно-практических проблем в области биологии, медицины и здравоохранения.
- 7. СТАТИСТИКА (Statistics)- наука о сборе, представлении и анализе данных. БИОСТАТИСТИКА - статистическая наука (statistics) в приложении
- 8. ВЕРОЯТНОСТЬ количественная мера объективной возможности появления события при реализации определенного комплекса условий. Вероятность события А обозначается
- 9. ДИЛЕММА НЕРЕШИТЕЛЬНОГО ВЛЮБЛЕННОГО МИСС А МИСС B МИСТЕР Z
- 10. ГЛАВНАЯ СТАНЦИЯ ОФИС МИСТЕРА Z Станция мисс В Станция мисс А
- 11. ГЛАВНАЯ СТАНЦИЯ ОФИС МИСТЕРА Z Станция мисс В Станция мисс А
- 12. ГЛАВНАЯ СТАНЦИЯ ОФИС МИСТЕРА Z Станция мисс В Станция мисс А Другие станции Другие станции
- 13. СЛУЧАЙНОЕ СОБЫТИЕ событие, которое при реализации определенного комплекса условий может произойти или не произойти. Его вероятность
- 14. ДОСТОВЕРНОЕ СОБЫТИЕ событие, которое при реализации определенного комплекса условий произойдет непременно. Его вероятность будет равна 1
- 15. НЕВОЗМОЖНОЕ СОБЫТИЕ событие, которое при реализации определенного комплекса условий не произойдет никогда. Его вероятность будет равна
- 16. ЧАСТОТА ПОЯВЛЕНИЯ СОБЫТИЯ (СТАТИСТИЧЕСКАЯ ВЕРОЯТНОСТЬ) это отношение числа случаев, в которых реализовался определенный комплекс условий (m),
- 17. ШАНС это отношение вероятности того, что событие произойдет к вероятности того, что событие не произойдет. ОТНОШЕНИЕ
- 18. ПРАВИЛО СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ Если два события, А и В, взаимоисключающие, несовместимые, то вероятность события А или
- 19. ПРАВИЛО УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ: Если два события, А и В, независимы (т.е. возникновение одного события не влияет
- 20. СЛУЧАЙНАЯ ВЕЛИЧИНА величина, которая при реализации определенного комплекса условий может принимать различные значения. Закон больших чисел:
- 21. Приступая к изучению основ статистического анализа необходимо выделить два основных этапа: - описание полученного в ходе
- 22. Основные направления применения математико-статистических методов в медицине и здравоохранении: Наиболее эффективный сбор данных и обобщение полученных
- 23. Прежде чем приступить к анализу данных и проверке различных гипотез: Сформулируйте вопрос, на который Вы хотите
- 24. Анализ организации конкретного исследования и его результатов: - оценить адекватность дизайна научного исследования решению той или
- 25. ЗНАНИЕ ВОЗМОЖНОСТЕЙ СТАТИСТИЧЕСКИХ МЕТОДОВ НЕОБХОДИМО КАЖДОМУ РАБОТАЮЩЕМУ В МЕДИЦИНЕ И ЗДРАВООХРАНЕНИИ.
- 26. Изучение статистики может пригодиться: При прочтении научных публикаций Важно понимать статистические исследования, проводимые в интересуемой области.
- 27. ПАКЕТЫ ПРИКЛАДНЫХ ПРОГРАММ: SPSS (Statistical Package for Social Science) SAS STATA STATISTICA BIOSTATISTICA Epilnfo программа «R»
- 28. ПРИМЕРЫ КЛИНИЧЕСКИХ ИССЛЕДОВАНИЙ Изучение эффективности нового лекарства Оценка нового диагностического теста Сравнительный анализ схем ведения больного
- 29. ЭТАПЫ НАУЧНО-ПРАКТИЧЕСКОГО ИССЛЕДОВАНИЯ: Формулирование цели и задач исследования. Организация исследования. Сбор информации. Обработка информации. Анализ результатов
- 30. Краткая и четкая цель I ЭТАП: ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ Этот этап включает в себя обоснование
- 31. I ЭТАП: ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ Название темы должно соответствовать цели исследования. Для раскрытия поставленной цели
- 32. I ЭТАП: ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ Большую помощь при формировании цели и задач исследования оказывает рабочая
- 33. I ЭТАП: ЦЕЛИ И ЗАДАЧИ ИССЛЕДОВАНИЯ Анализ литературы помогает: Оценить степень разработки темы; Определить дизайн исследования
- 34. II ЭТАП: ОРГАНИЗАЦИЯ ИССЛЕДОВАНИЯ (DESIGN STUDY)
- 35. II ЭТАП: ОРГАНИЗАЦИЯ ИССЛЕДОВАНИЯ Выбор объекта наблюдения: Под объектом наблюдения понимают статистическую совокупность, состоящую из отдельных
- 36. II ЭТАП: ОРГАНИЗАЦИЯ ИССЛЕДОВАНИЯ Единица наблюдения – первичный элемент статистической совокупности, являющийся носителем признаков (variables), подлежащих
- 37. II ЭТАП: ОРГАНИЗАЦИЯ ИССЛЕДОВАНИЯ Типы признаков (виды шкал): Переменные Категориальные (качественные) Номинальные Порядковые (ординальные) Числовые (количественные)
- 38. II ЭТАП: ОРГАНИЗАЦИЯ ИССЛЕДОВАНИЯ Перечень признаков, подлежащих изучению в ходе исследования, оформляется в виде регистрационного документа
- 39. II ЭТАП: ОРГАНИЗАЦИЯ ИССЛЕДОВАНИЯ В зависимости от степени охвата объекта исследования принято различать: сплошное исследование (генеральная
- 40. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ Это совокупность всех мыслимо возможных объектов данного вида, над которыми проводятся наблюдения с целью
- 41. РЕПРЕЗЕНТАТИВНОСТЬ Репрезентативность означает, что все пропорции генеральной совокупности должны быть представлены в выборке. Репрезентативность выборки обеспечивается
- 42. II ЭТАП: ОРГАНИЗАЦИЯ ИССЛЕДОВАНИЯ репрезентативность – это представительность выборочной совокупности по отношению ко всей (генеральной) совокупности;
- 43. II ЭТАП: ОРГАНИЗАЦИЯ ИССЛЕДОВАНИЯ Репрезентативность выборки зависит от … Главное требование, предъявляемое к отбору - …
- 44. РАНДОМИЗАЦИЯ Процесс создания репрезентативной выборки достигается путем рандомизации (random - случайный (англ.)), т.е. процессом случайного отбора
- 45. МЕТОДЫ СЛУЧАЙНОГО ОТБОРА ОБЪЕКТОВ Механический отбор с повтором и без повтора. Отбор с помощью таблиц или
- 46. МЕТОДЫ СЛУЧАЙНОГО ОТБОРА ОБЪЕКТОВ Кластерная выборка – похожа на многоступенчатую, отличие состоит в том, что исследуются
- 47. II ЭТАП: ОРГАНИЗАЦИЯ ИССЛЕДОВАНИЯ Важное место при решении организационных вопросов исследования принадлежит так называемому пробному, предварительному
- 48. III ЭТАП: СБОР ИНФОРМАЦИИ На этом этапе основное внимание должно быть уделено соблюдению правил регистрации, охвату
- 49. III ЭТАП: СБОР ИНФОРМАЦИИ Способы сбора данных: отчетный (с помощью системы учетно-отчетной документации); экспедиционный (при обследовании
- 50. IV ЭТАП: ОБРАБОТКА ДАННЫХ СОЗДАНИЕ И ПОДГОТОВКА БАЗЫ ДАННЫХ
- 51. V ЭТАП: АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ
- 52. ТИПЫ ПРИЗНАКОВ (ВИДЫ ШКАЛ): Переменные Категориальные (качественные) Номинальные Порядковые (ординальные) Числовые (количественные) Дискретные Непрерывные
- 53. Типы признаков (виды шкал): Качественные категориальные (qualititative, categorical) Номинальные (Nominal); Дихотомические (Binary - dichotomous); Порядковые, ординальные,
- 54. РАЗЛИЧИЕ МЕЖДУ ТИПАМИ ДАННЫХ В зависимости от того, оказываются ли данные категориальными или числовыми, используют различные
- 55. ПРОИЗВОДНЫЕ (ВТОРИЧНЫЕ) ДАННЫЕ Проценты. Могут возникать при рассмотрении вопроса относительно улучшения состояния больного во время лечения.
- 56. ЦЕНЗУРИРОВАННЫЕ ДАННЫЕ Мы можем рассмотреть цензурированные данные на следующих примерах. - Если мы проводим лабораторные измерения,
- 57. ФОРМАТЫ ВВОДА ДАННЫХ Существует несколько способов ввода данных и сохранения их в компьютере. Большинство статистических пакетов
- 58. КАТЕГОРИАЛЬНЫЕ ДАННЫЕ С нечисловыми данными могут возникнуть проблемы при занесении их в некоторые статистические пакеты, поэтому
- 59. ЧИСЛОВЫЕ ДАННЫЕ Должны быть введены с той же самой точностью, с которой были проведены измерения, и
- 60. МНОЖЕСТВЕННЫЕ ФОРМЫ НА ОДНОГО БОЛЬНОГО Иногда информацию собирают на одного и того же больного более чем
- 61. КОДИРОВАНИЕ ОТСУТСТВУЮЩИХ (ПРОПУЩЕННЫХ) ДАННЫХ Вам следует определить, что вы будете делать с отсутствующими данными, прежде чем
- 62. ПРОВЕРКА ОШИБОК И ВЫБРОСОВ При любом исследовании всегда есть опасность допустить ошибки при наборе данных либо
- 63. ВЫБРОСЫ (АНОМАЛЬНЫЕ ЗНАЧЕНИЯ) Наблюдения, которые отличаются от главной группы данных и несовместимы с остальными. Эти данные
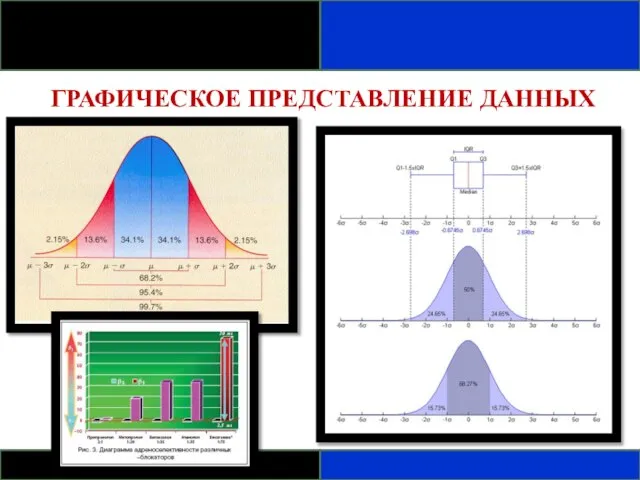
- 64. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
- 65. СТОЛБЧАТАЯ И КОЛОНЧАТАЯ ДИАГРАММА
- 66. КРУГОВАЯ ДИАГРАММА
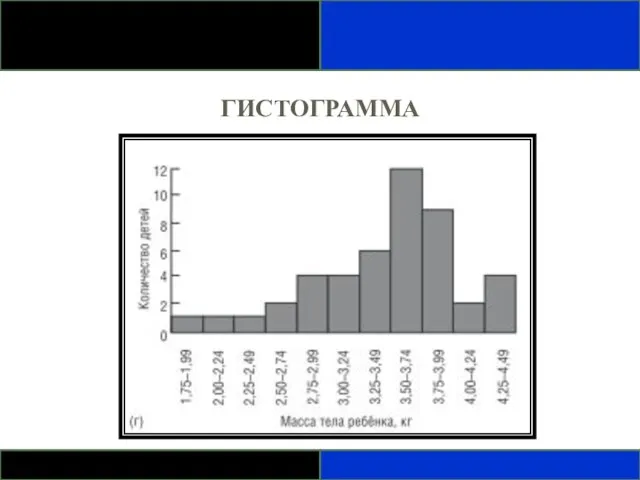
- 67. ГИСТОГРАММА
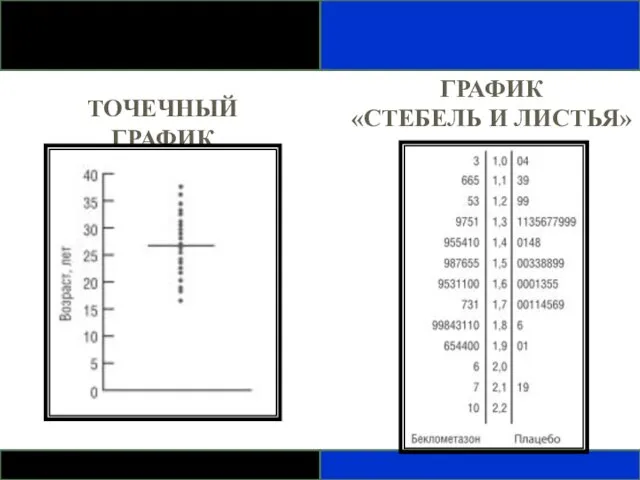
- 68. ТОЧЕЧНЫЙ ГРАФИК ГРАФИК «СТЕБЕЛЬ И ЛИСТЬЯ»
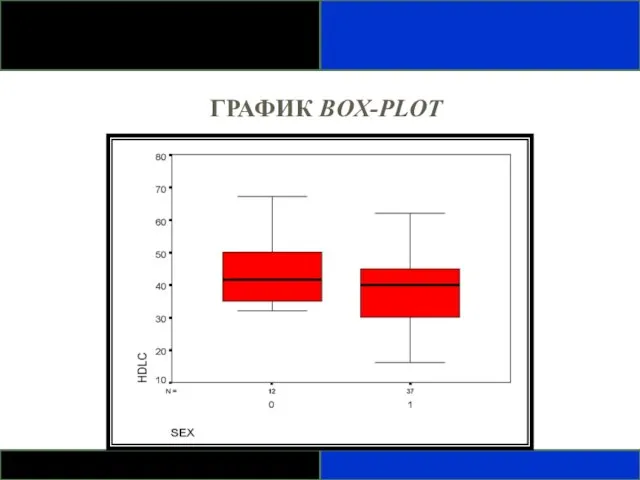
- 69. ГРАФИК BOX-PLOT
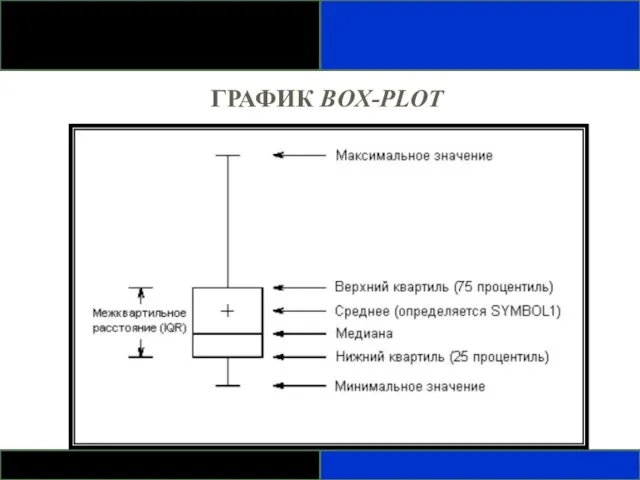
- 70. ГРАФИК BOX-PLOT
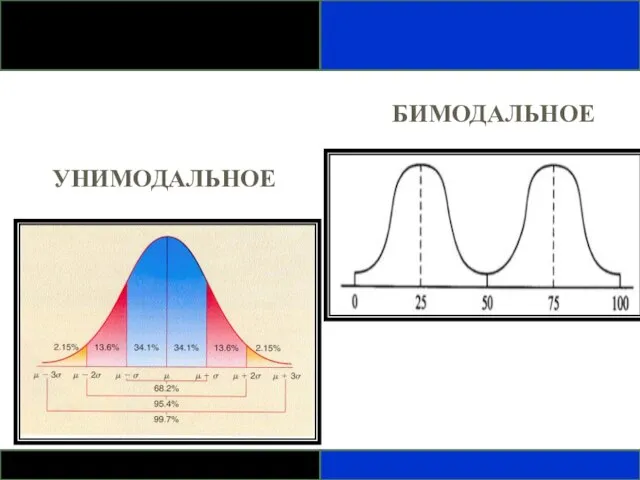
- 71. ФОРМЫ ЧАСТОТНОГО РАСПРЕДЕЛЕНИЯ Выбор наиболее подходящего статистического метода часто зависит от формы распределения. Распределение данных чаще
- 72. БИМОДАЛЬНОЕ УНИМОДАЛЬНОЕ
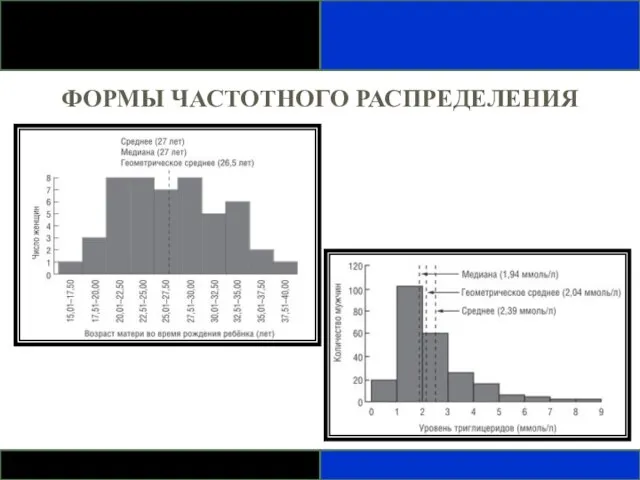
- 73. ФОРМЫ ЧАСТОТНОГО РАСПРЕДЕЛЕНИЯ
- 74. ПОКАЗАТЕЛИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ПОКАЗАТЕЛИ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ Среднее (average, mean) Мода (mode) Медиана (median) ПОКАЗАТЕЛИ РАЗБРОСА ДАННЫХ
- 75. ОПИСАНИЕ ДАННЫХ: «МЕРЫ ПОЛОЖЕНИЯ» СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ Одна из мер центральной тенденции. Вычисляется путем суммирования всех величин
- 76. ОПИСАНИЕ ДАННЫХ: «МЕРЫ ПОЛОЖЕНИЯ» СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ (Μ - M) Используя математическую систему обозначения, мы можем сократить
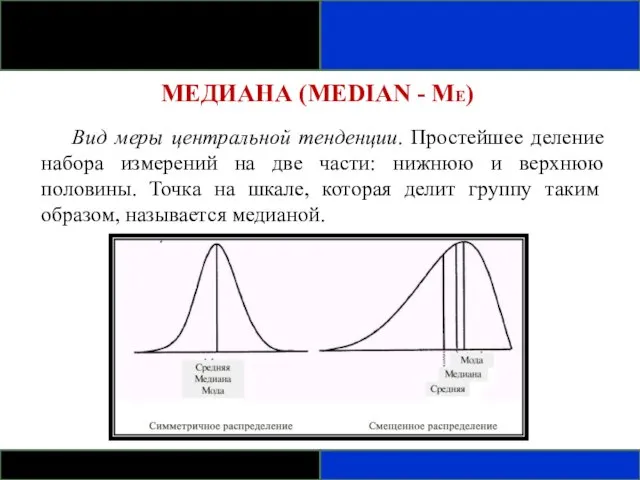
- 77. МЕДИАНА (MEDIAN - ME) Вид меры центральной тенденции. Простейшее деление набора измерений на две части: нижнюю
- 78. МОДА (MODE - MO) Вид меры центральной тенденции. Наиболее часто встречающееся значение среди набора наблюдений. Мода
- 79. СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ (GEOMETRIC MEAN) Одна из мер центральной тенденции. Вычисляется суммированием логарифмов всех величин в группе,
- 80. ОПИСАНИЕ ДАННЫХ: «МЕРЫ РАССЕЯНИЯ» РАЗМАХ (ИНТЕРВАЛ ИЗМЕНЕНИЯ) Разность между максимальным и минимальным значениями переменной в наборе
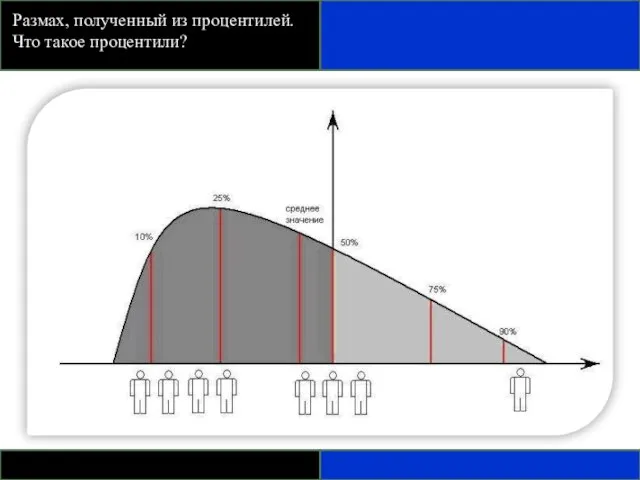
- 81. Размах, полученный из процентилей. Что такое процентили?
- 82. ПРИМЕНЕНИЕ ПРОЦЕНТИЛЕЙ Межквартильный размах – разница между первым и третьим квартилем, т.е. между 25-м и 75-м
- 83. ДИСПЕРСИЯ (ОТ ЛАТ. – DISPERSES – РАССЕЯННЫЙ, РАССЫПАННЫЙ) Один из способов измерения рассеяния данных заключается в
- 84. СТАНДАРТНОЕ ОТКЛОНЕНИЕ Стандартное (среднее квадратичное) отклонение – положительный квадратный корень из дисперсии. На примере n наблюдений
- 85. ПОНИМАНИЕ ВЕРОЯТНОСТИ МОЖНО ВЫЧИСЛИТЬ ВЕРОЯТНОСТЬ, ИСПОЛЬЗУЯ РАЗЛИЧНЫЕ ПОДХОДЫ: - СУБЪЕКТИВНАЯ; - ЧАСТОТНАЯ; - АПРИОРНАЯ.
- 86. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ: ТЕОРИЯ Случайная величина – это величина, которая может принимать любое из набора взаимоисключающих значений
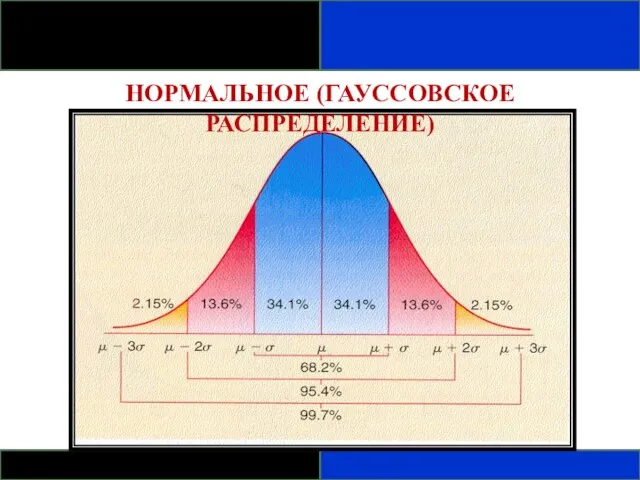
- 87. НОРМАЛЬНОЕ (ГАУССОВСКОЕ РАСПРЕДЕЛЕНИЕ) Одно из самых важных распределений в статистике – нормальное распределение. Его функция плотности
- 88. НОРМАЛЬНОЕ (ГАУССОВСКОЕ РАСПРЕДЕЛЕНИЕ) ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА Среднее и медиана нормального распределения равны. Вероятность того, что нормально распределенная
- 89. НОРМАЛЬНОЕ (ГАУССОВСКОЕ РАСПРЕДЕЛЕНИЕ)
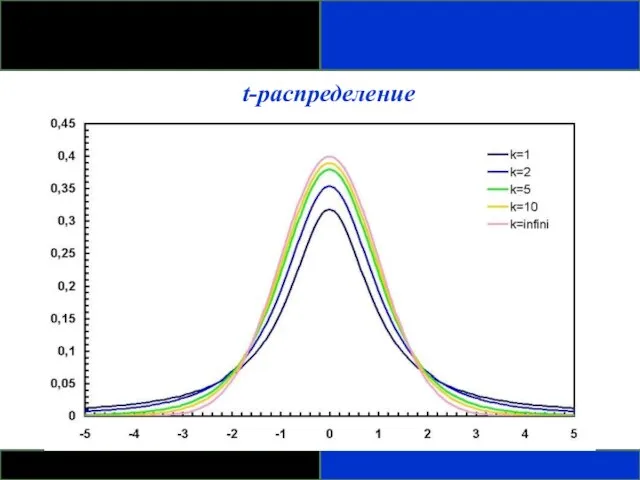
- 90. ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ: ДРУГИЕ РАСПРЕДЕЛЕНИЯ t-распределение - Получено Вильямом Госсетом, который публиковался под псевдонимом Студент (Student), поэтому
- 91. t-распределение
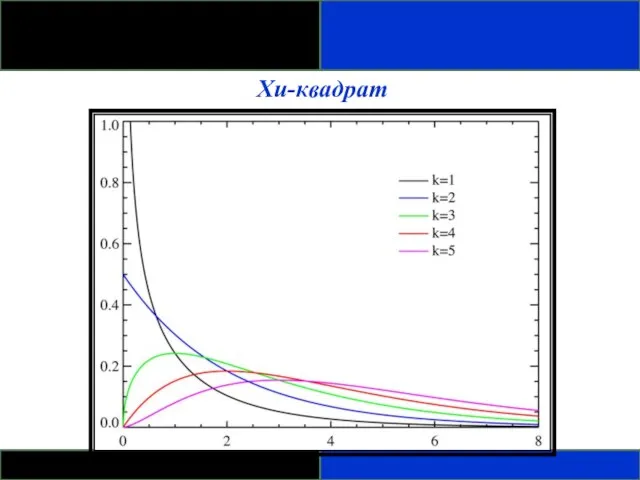
- 92. ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ: ДРУГИЕ РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ Хи-квадрат Хи-квадрат, (χ2) или распределение Пирсона: - скошено вправо
- 93. Хи-квадрат
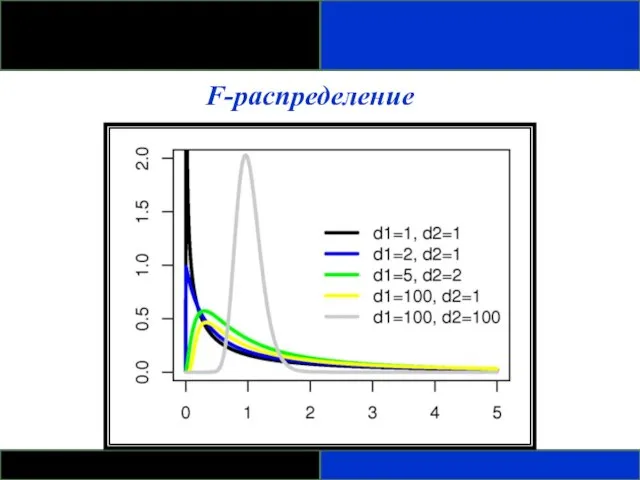
- 94. F-распределение - Скошено вправо. - Определяется как отношение. Распределения отношения двух оценок дисперсий, вычисленных для нормально
- 95. F-распределение
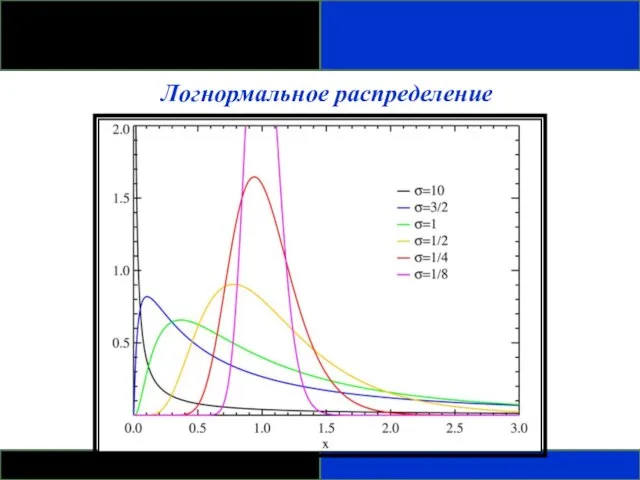
- 96. Логнормальное распределение - Распределение вероятности случайной переменной, логарифм которого (по основанию 10 или более е –
- 97. Логнормальное распределение
- 98. ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ: ДРУГИЕ РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫЕ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
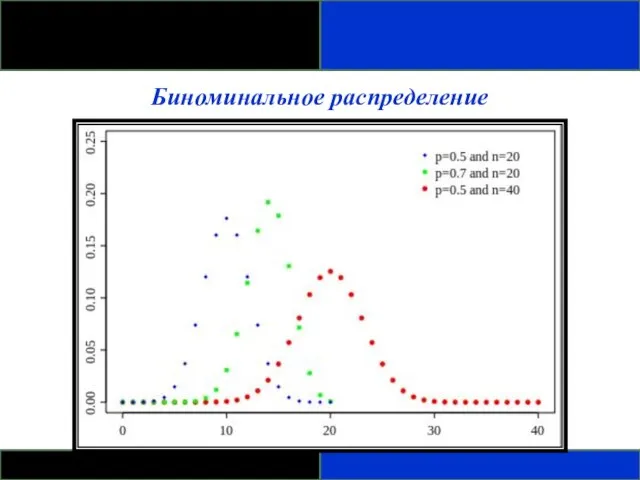
- 99. Биноминальное распределение
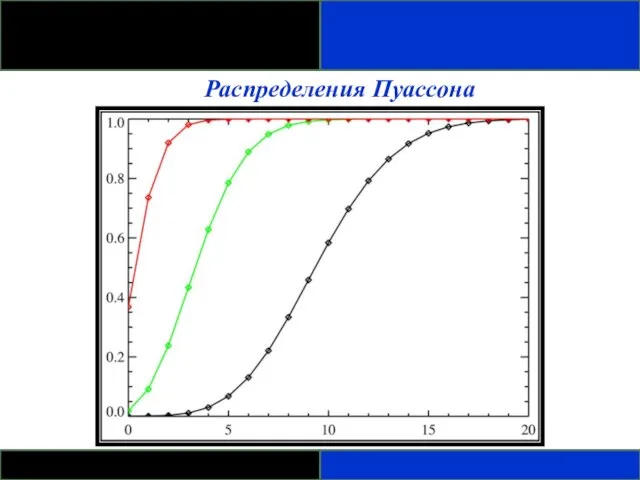
- 100. Распределения Пуассона - Пуассоновская случайная переменная – число событий, которые происходят независимо и случайно во времени
- 101. Распределения Пуассона
- 102. КАК ОПИСАТЬ ДАННЫЕ? Если значения интересующего нас признака у большинства объектов близки к их среднему и
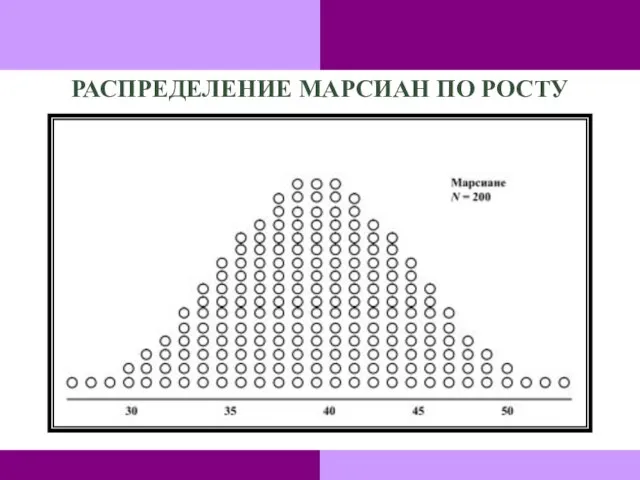
- 103. РАСПРЕДЕЛЕНИЕ МАРСИАН ПО РОСТУ
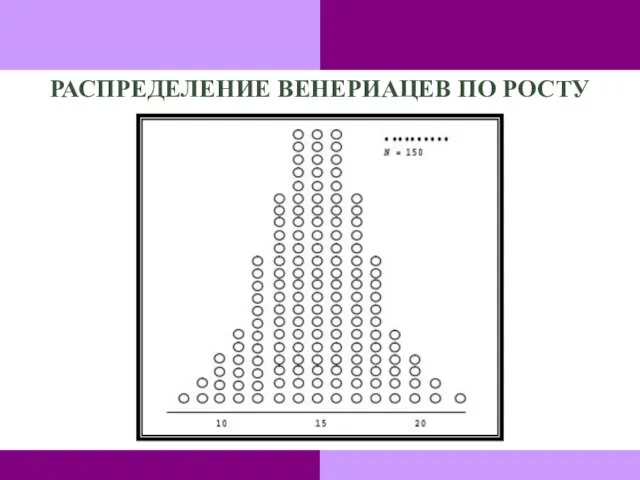
- 104. РАСПРЕДЕЛЕНИЕ ВЕНЕРИАЦЕВ ПО РОСТУ
- 105. ПАРАМЕТРЫ РАСПРЕДЕЛЕНИЯ МАРСИАН И ВЕНЕРИАЦЕВ
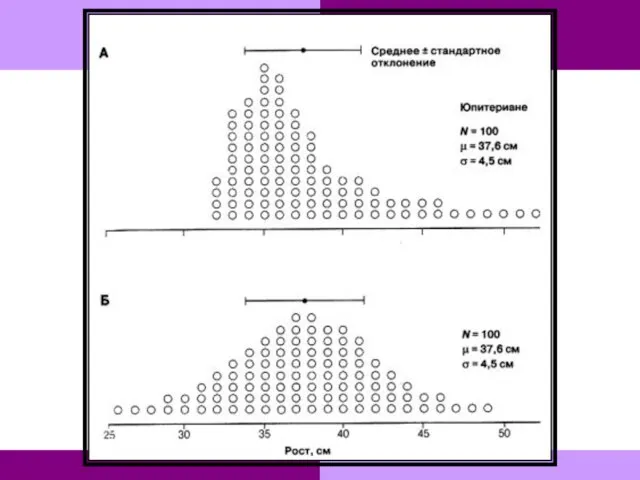
- 107. Если распределение асимметрично полагаться на среднее и стандартное отклонение нельзя. А. Распределение юпитериан по росту. Б.
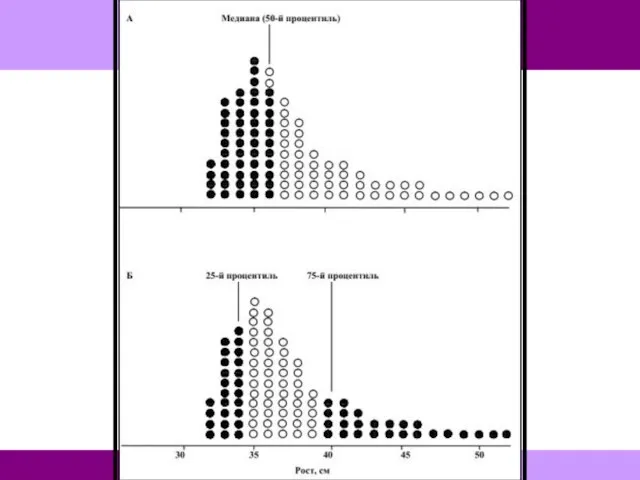
- 109. Для описания асимметричного распределения следует использовать медиану и процентили. Медиана — это значение, которое делит распределение
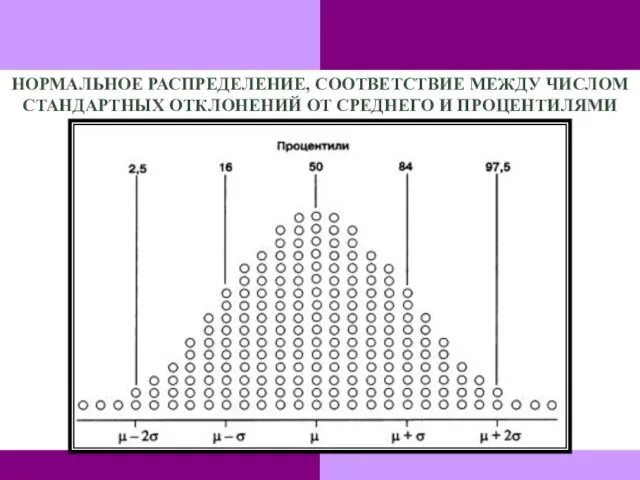
- 110. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, СООТВЕТСТВИЕ МЕЖДУ ЧИСЛОМ СТАНДАРТНЫХ ОТКЛОНЕНИЙ ОТ СРЕДНЕГО И ПРОЦЕНТИЛЯМИ
- 111. А в чем проблема? Вариабельность Случайная Систематическая
- 113. Статистика Описательная Графические методы Суммирование данных Статистические выводы Статистические модели Проверка гипотез Поиск закономерностей (data mining)
- 114. Статистические выводы цель статистики: аппроксимация истины некоторые определения различия между статистической и клинической значимостью
- 115. Позиция #1. Статистика как отражение истины Статистическая значимость не истина, а "аппроксимация" истины Истина Что мы
- 116. Позиция #2. Пользователи статистики не должны быть профессиональными статистиками Вам не надо знать много о статистике,
- 117. P Алтарь статистики Священная P-оценка
- 118. P оценка "Probability" Вероятность того, что различия между двумя группами возникли случайно Искусственно фиксирована на уровне
- 119. P оценка Зависит от нескольких факторов. Насколько был большим эффект. Насколько одинаковым был эффект у обследованных.
- 120. Извлечение информации из р-оценки "Высоко значимая" — P Если количество пациентов небольшое, р-оценка свидетельствует о том,
- 121. “Не значимо” P > 0.05 (например, 0.15) Если количество пациентов мало, их может быть просто недостаточно
- 122. "Пограничная значимость" — P = 0.08 — ???? Могли бы достичь значимости, если бы в исследовании
- 123. Статистика в медицинских исследованиях Логика научного метода Дедуктивная логика (выдвигается гипотеза, затем собираются факты) - от
- 124. Нулевая гипотеза Предполагаем, что различий нет Собираем данные и оцениваем существующие различия Если нулевая гипотеза справедлива,
- 125. Альтернативная гипотеза Между группами существуют различия (но мы не можем сказать, какой величины)
- 126. Ошибки при статистическом выводе Альфа ошибка (вероятность отвергнуть нулевую гипотезу, если на самом деле она справедлива)
- 127. Доверительные интервалы "Статистика статистики" статистические показатели - это оценки Доверительные интервалы показывают нам границы нашей оценки
- 128. Доверительный интервал Интервал, в котором с заданной вероятностью (обычно 95%) находится популяционное среднее значение
- 130. Скачать презентацию







































































































 Обобщающий урок по творчеству А.С.Пушкина
Обобщающий урок по творчеству А.С.Пушкина Флаг России
Флаг России Unit01_TS625
Unit01_TS625 Mixed conditionals
Mixed conditionals Информация по поступлению в 2021 году
Информация по поступлению в 2021 году Политический экстремизм. Как его избежать?
Политический экстремизм. Как его избежать? www.silentium.ru
www.silentium.ru Задачи практического содержания
Задачи практического содержания Общая характеристика, назначение и область применения транспортирующих машин без тягового органа
Общая характеристика, назначение и область применения транспортирующих машин без тягового органа Изучение Мирового океана
Изучение Мирового океана Внеклассное мероприятие «Прощай, второй класс»
Внеклассное мероприятие «Прощай, второй класс» Презентация на тему Мировоззрение средневекового человека
Презентация на тему Мировоззрение средневекового человека Модели реформирования системы водоснабжения и водоотведения г.Москвы и ее перспективное развитие Докладчик: Заместитель генер
Модели реформирования системы водоснабжения и водоотведения г.Москвы и ее перспективное развитие Докладчик: Заместитель генер Хранитель памяти
Хранитель памяти Technika klejenia
Technika klejenia НАШИ ВОЗМОЖНОСТИ
НАШИ ВОЗМОЖНОСТИ Грузинский Технический Университет. Тбилиси
Грузинский Технический Университет. Тбилиси Презентация на тему Трансформатор. Передача электрической энергии на расстояние
Презентация на тему Трансформатор. Передача электрической энергии на расстояние  Занятие по физике в 6 классе «Энергетическое будущее – 2030»
Занятие по физике в 6 классе «Энергетическое будущее – 2030» Дерево из бисера «Сосна»
Дерево из бисера «Сосна» Артюх Елена Николаевна Генеральный директор ЗАО Юридическая фирма «ЛЕВЪ» ируководитель Группы компаний «ЛЕВЪ&ЛЕВЪ-АУДИТ»
Артюх Елена Николаевна Генеральный директор ЗАО Юридическая фирма «ЛЕВЪ» ируководитель Группы компаний «ЛЕВЪ&ЛЕВЪ-АУДИТ» Факты и цифры о компании Год основания компании – 1994 Штат – более 300 человек Входит в пятерку крупнейших автоматизаторов торговли
Факты и цифры о компании Год основания компании – 1994 Штат – более 300 человек Входит в пятерку крупнейших автоматизаторов торговли  ФОНД«ИНСТИТУТ ЭКОНОМИКИ ГОРОДА»
ФОНД«ИНСТИТУТ ЭКОНОМИКИ ГОРОДА» Единая Система Муниципальных Сайтов
Единая Система Муниципальных Сайтов Целеполагание в бизнесе
Целеполагание в бизнесе Продукт. Мобильное приложение. Курсы. Ноу-хау в сфере образования в Казахстане. Курсы на казахском языке
Продукт. Мобильное приложение. Курсы. Ноу-хау в сфере образования в Казахстане. Курсы на казахском языке Предоставляемые территориальными органами Фонда услуги по регистрации и снятию с регистрационного учета
Предоставляемые территориальными органами Фонда услуги по регистрации и снятию с регистрационного учета Мы - это частица России
Мы - это частица России