Хекало Владислав 5 Г класс МОУ СОШ №1 г.Пугачев

Составление магических квадратов представляет собой превосходную развивающую способность понимать идеи размещения, сочетания, симметрии, классификации, обобщения и т.д.
А. Обри

Исторические значимые магические квадраты
Магический квадрат – древнекитайского происхождения. Согласно легенде, во время правления императора Ю из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы

Магическая константа
Сумма чисел в каждой строке, столбце и на диагоналях называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой

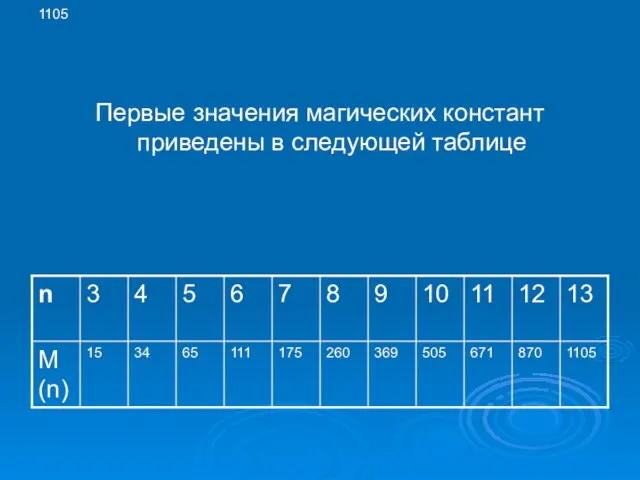
1105
Первые значения магических констант приведены в следующей таблице

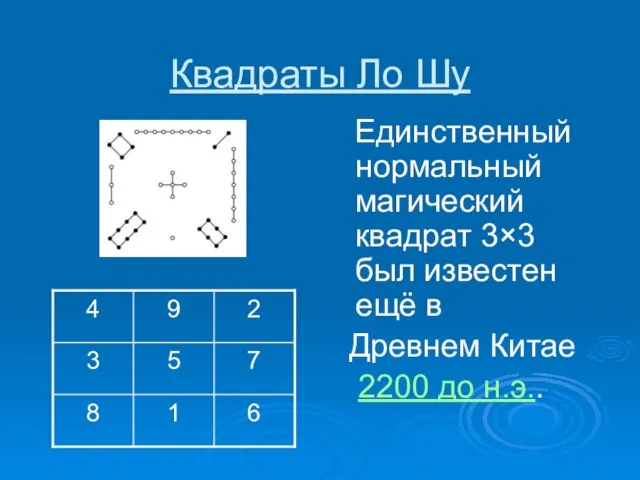
Квадраты Ло Шу
Единственный нормальный магический квадрат 3×3 был известен ещё в
Древнем Китае
2200 до н.э..

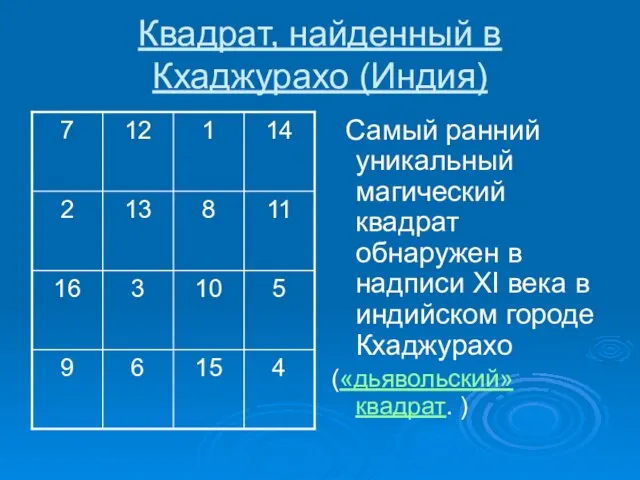
Квадрат, найденный в Кхаджурахо (Индия)
Самый ранний уникальный магический квадрат обнаружен в надписи XI века в индийском городе Кхаджурахо
(«дьявольский» квадрат. )

Квадрат Альбрехта Дюрера
Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера«Меланхолия», считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания картины (1514).

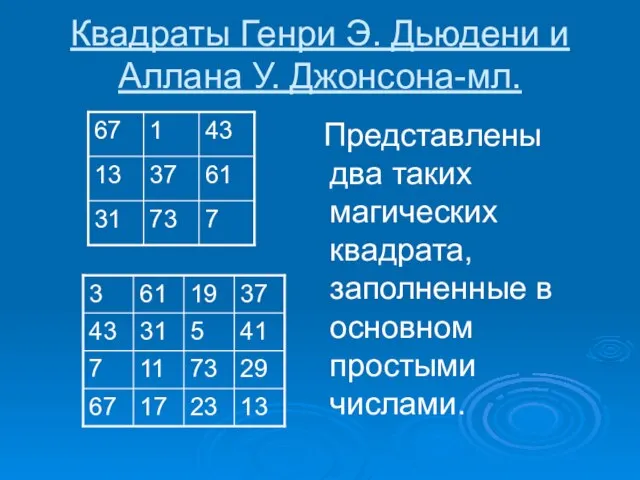
Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл.
Представлены два таких магических квадрата, заполненные в основном простыми числами.

Построение магических квадратов
Метод террас описан Ю. В. Чебраковым в «Теории магических матриц». Я нашел и более простой и доступный метод построения в книге «Волшебный мир логических квадратов» нашей землячки Макаровой М. В.

Метод террас

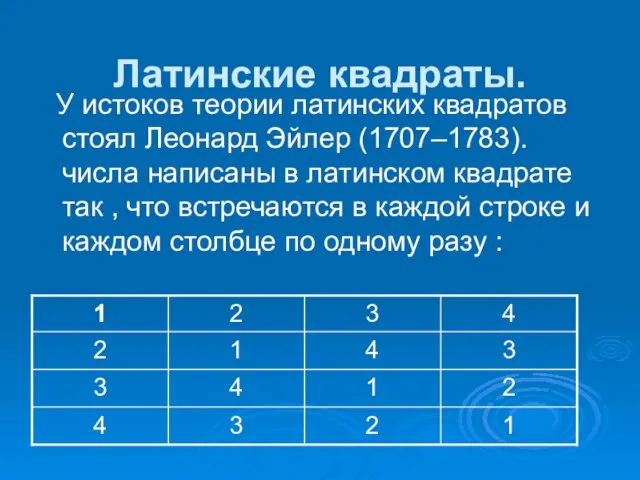
Латинские квадраты.
У истоков теории латинских квадратов стоял Леонард Эйлер (1707–1783). числа написаны в латинском квадрате так , что встречаются в каждой строке и каждом столбце по одному разу :

Использование латинских квадратов для планирования экспериментов
Латинские квадраты нашли многочисленные применения как в математике, так и в ее приложениях при постановке и обработке результатов экспериментов.