Задачи на смеси, растворы и сплавы

Проблема:
задачи на смеси, растворы и сплавы вызывают большие затруднения у выпускников.

Цель:
научится решать задачи на смеси, растворы и сплавы, а также составить дидактический материал.

Задачи:
Собрать теоретический материал.
Рассмотреть методы решения задач.
Создать дидактический материал.

Как известно, в основе методики решения этих задач лежит связь между тремя величинами в виде прямой и обратной зависимостей:
S = VT
T =
-
S
V
V =
-
S
T
A = VT
T =
-
V
A
V
=
A
-
T
- для количества работы А, времени Т и производительности V
- для пути S, времени T и скорости V;

Кроме того, применяются некоторые правила:
сложение или вычитание скоростей при движении в движущейся среде, сложение или вычитание производительностей при совместной работе и др.

Основные понятия в
задачах на смеси,
растворы и сплавы

«Смесь»
«Чистое вещество»
«Примесь»
Доли чистого вещества в смеси – «a»
Чистое вещество – «m»
Общее количество – «М»
a = m : M m = a M M= m : a

Отметим, что 0 ≤ a ≤ 1, ввиду того, что 0 ≤ m ≤ M. Случай a=0 соответствует отсутствию выбранного чистого вещества в рассматриваемой смеси (m=0), случай a =1 соответствует тому, что рассматриваемая смесь состоит только из чистого вещества (m= M).

Понятие доли чистого вещества в смеси можно вводить следующей условной записью:
Доля чистого вещества в смеси
=
=
_
Количество чистого вещества в смеси
Общее количество смеси

Процентное содержание чистого вещества в смеси – «с»
c = a · 100%, a = c:100%

При решении задач следует руководствоваться тем, что при соединении (разъединении) смесей с одним и тем же чистым веществом количества чистого вещества и общие количества смесей складываются (вычитаются). Складывать и вычитать доли и процентные содержания нельзя.

Выбор неизвестной (или неизвестных).
Выбор чистого вещества.
Переход к долям.
Отслеживание состояния смеси.
Составление уравнения.
Решение уравнения (или их системы).
Формирование ответа.
Основные этапы решения задач

В ходе осуществления этих этапов рекомендую ввести следующую таблицу:

Задача 1. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация составляла 1,5%?
Примеры решения задач

Решение:
Пусть требуется добавить x кг пресной воды.
За чистое вещество примем соль. Тогда морская вода – это смесь с 5%-ным содержанием чистого вещества, пресная вода – с 0%-ным содержанием чистого вещества.
Переходя долям, получаем, что доля соли в морской воде составляет 0,05, доля соли в пресной воде равна 0, доля в смеси, которую нужно получить, – 0,015.

Происходит соединение смесей.

Исходя из третьей строки таблицы, составим уравнение m = a M : 0,05 · 30 = 0,015(30 + x).
Решим полученное уравнение и находим x = 70.
В данной задаче не содержалось требования найти процентное содержание какого-либо вещества, поэтому нет необходимости переводить доли в процентные содержания.
Ответ: 70 кг.

Задача 2. Смешали 30%-ный раствор соляной кислоты с 10%-ным и получили 600 г 15%-ного раствора. Сколько граммов каждого вещества было взято?
Решение: Пусть взяли x г первого раствора, тогда второго раствора (600 – x) г.

Тогда 0,3 x + 0,1(600 – x) = 0,15 · 600, откуда x = 150, 600 – x = 450.
Ответ: 150 г 30%-ного раствора,
450 г 10%-ного раствора.

Задача 3. Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 25% цинка, а второй – 50% меди. Процентное содержание олова в первом сплаве в 2 раза выше, чем во втором. Сплавив 200 кг первого и 300 кг второго, получили новый сплав, в котором оказалось 28% олова. Определить, сколько килограммов меди содержится в получившемся новом сплаве.
Пример усложненной задачи

Решение. Пусть x – доля олова во II сплаве, тогда 2x – доля олова в I сплаве. Сначала определим долю олова в данных сплавах. Для этого заполним таблицу, выполнив переход от процентных содержаний к долям.

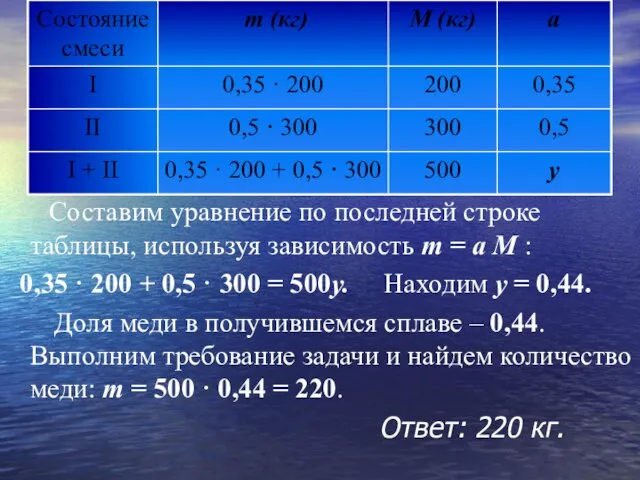
Становится очевидным, что уравнение можно составить по последней строке таблицы, используя зависимость m = a M :
2 · x · 200 + x · 300 = 0,28 · 500, откуда x = 0,2.
Таким образом, доля олова в первом сплаве будет 0,4, а во втором – 0,2.
Теперь выберем в качестве чистого вещества медь, и пусть y – доля меди в получившемся сплаве.
Сосчитаем по таблице долю меди в первом сплаве
1 – (0,25 + 0,4) = 0,35.
Составим таблицу (относительно меди).

Составим уравнение по последней строке таблицы, используя зависимость m = a M :
0,35 · 200 + 0,5 · 300 = 500y. Находим y = 0,44.
Доля меди в получившемся сплаве – 0,44. Выполним требование задачи и найдем количество меди: m = 500 · 0,44 = 220.
Ответ: 220 кг.