Площади фигур

Площади фигур
Основные теоретические сведения
Задачи с решениями
Задачи для самостоятельного решения

Основные теоретические сведения
Площадь треугольника
Площадь параллелограмма
Площадь
ромба
Площадь квадрата
Площадь трапеции
Площадь прямоугольника

Площадь треугольника
Произвольный треугольник
Прямоугольный треугольник
Равносторонний треугольник

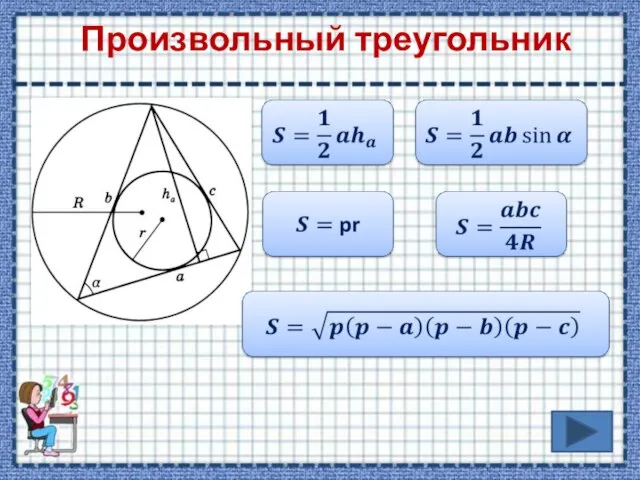
Произвольный треугольник

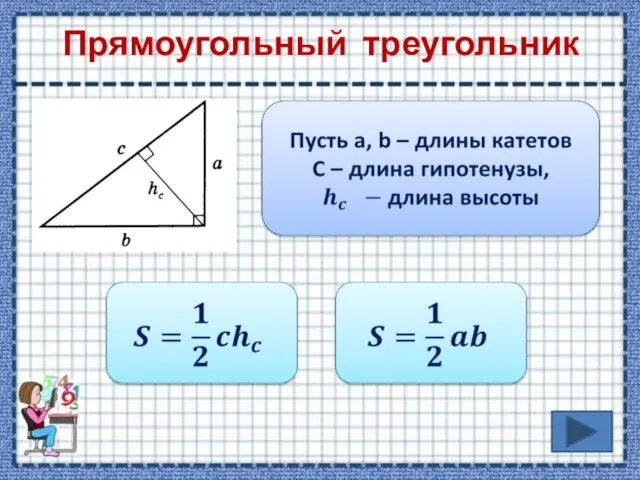
Прямоугольный треугольник

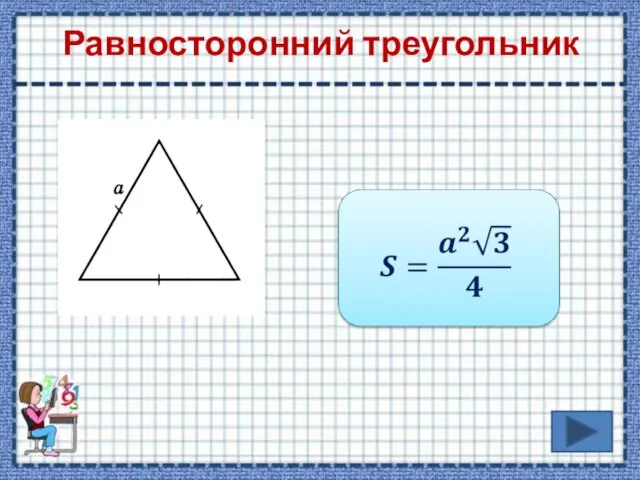
Равносторонний треугольник

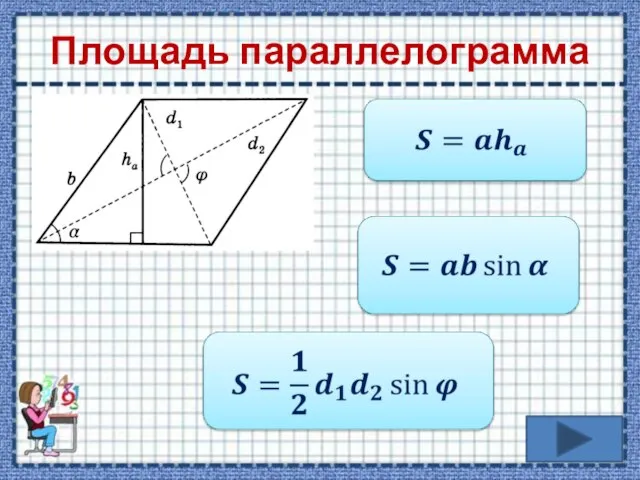
Площадь параллелограмма

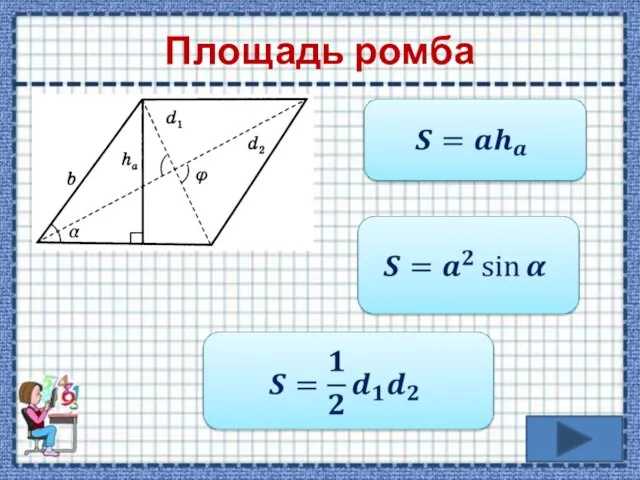
Площадь ромба

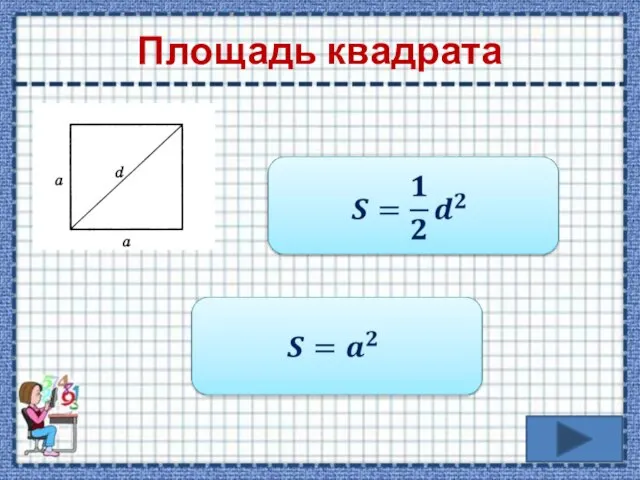
Площадь квадрата

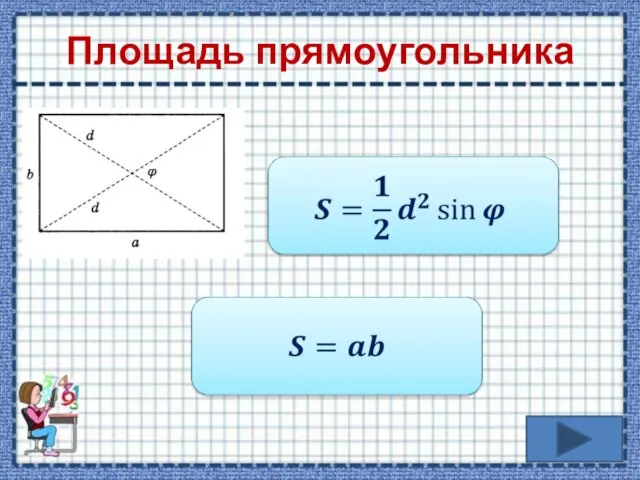
Площадь прямоугольника

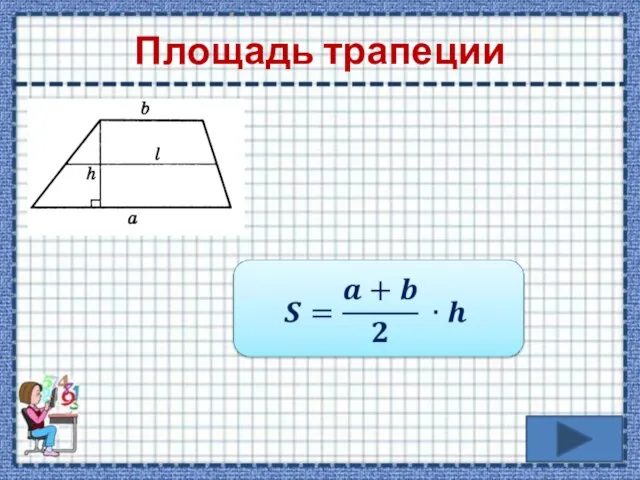
Площадь трапеции

Задачи с решениями
Задача 1
Задача 2
Задача 3

Найти площадь треугольника АВС
Решение
Решение .
Катет ВС, расположенный против угла в 30⁰ равен половине гипотенузы, следовательно, ВС = 8. площадь можно найти различными способами, например, по формуле

Решение
Продолжение

Медиана прямоугольного треугольника равна половине гипотенузы, значит она разбила исходный треугольник на 2 равнобедренных с боковыми сторонами 1, у одного из которых угол при вершине 60⁰, у другого 120⁰.
Медиана прямоугольного треугольника, проведенная к гипотенузе, имеет длину 1 и образует с гипотенузой угол 60⁰. Найдите площадь треугольника.
Решение

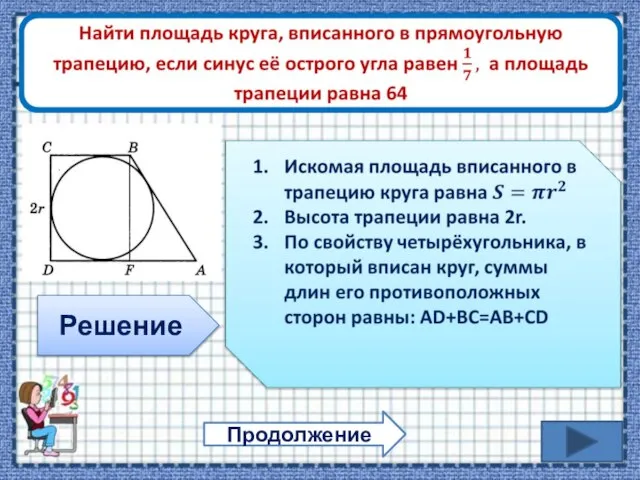
Задачи для самостоятельного решения
Найти площадь круга, вписанного в равнобедренную трапецию площади, равной 8, если боковая сторона трапеции в 2 раза больше её высоты.
ответ
Площадь равнобедренной трапеции равна 96. диагональ трапеции делит её тупой угол пополам. Длина меньшего основания равна 3. найти периметр трапеции
ответ
42
ответ