Содержание
- 2. Происхождение задачи о лабиринтах Слово «лабиринт» — греческое и в переводе означает ходы в подземельях.
- 3. Природные подземные пещеры Искусственные лабиринты
- 4. Лабиринт Дедала Лабиринты бывают самой разнообразной формы и устройства.
- 5. Во Франции того времени лабиринты выкладывались из камня или изображались на полу церквей и соборов. Они
- 6. «Город Троя» Лабиринты в Англии «Следы пастуха» В Англии не встречаются лабиринты на церковном полу, но
- 7. Лабиринты
- 8. «Дерновый» лабиринт (33—34 м в диаметре), просуществовавший до 1797 года в Англии в графстве Эссекс. Итальянский
- 9. Леонард Эйлер
- 10. Геометрическая постановка задачи о лабиринтах Аллеи, дорожки, коридоры и т. п. лабиринты тянутся, изгибаясь во все
- 11. Правило 1. Отправляемся от выбранной вершины (первого перекрестка) и идем по любому ребру, пока не приходим
- 12. замечания: Выходя из точки отправления, скажем А, мы ставим начальный знак (поперечную черточку). Прохождение через перекресток
- 13. 2. Беседка А теперь, для вас будет нетрудно найти путь к беседке, расположенной в парке, изображенном
- 15. Скачать презентацию
Слайд 2Происхождение задачи о лабиринтах
Слово «лабиринт» — греческое и в переводе означает ходы
Происхождение задачи о лабиринтах
Слово «лабиринт» — греческое и в переводе означает ходы

Слайд 3Природные
подземные
пещеры
Искусственные
лабиринты
Природные
подземные
пещеры
Искусственные
лабиринты

Слайд 4Лабиринт Дедала
Лабиринты бывают самой разнообразной формы и устройства.
Лабиринт Дедала
Лабиринты бывают самой разнообразной формы и устройства.

Слайд 5Во Франции того времени лабиринты выкладывались из камня или изображались на полу
Во Франции того времени лабиринты выкладывались из камня или изображались на полу

Лабиринт, выложенный из камня на
полу храма святого Квентина во Франции.
Вход снизу по вертикальной линии
Лабиринт в Шартрском соборе во Франции.
Слайд 6«Город Троя»
Лабиринты в Англии
«Следы пастуха»
В Англии не встречаются лабиринты на церковном
«Город Троя»
Лабиринты в Англии
«Следы пастуха»
В Англии не встречаются лабиринты на церковном

Слайд 7Лабиринты
Лабиринты

Слайд 8«Дерновый» лабиринт (33—34 м в диаметре),
просуществовавший до 1797 года в Англии
«Дерновый» лабиринт (33—34 м в диаметре),
просуществовавший до 1797 года в Англии

Итальянский лабиринт XVI столетия.
Слайд 9Леонард
Эйлер
Леонард
Эйлер

Слайд 10Геометрическая постановка задачи о лабиринтах
Аллеи, дорожки, коридоры и т. п. лабиринты тянутся,
Геометрическая постановка задачи о лабиринтах
Аллеи, дорожки, коридоры и т. п. лабиринты тянутся,

Эти точки и эти линии вместе составляют геометрическую сеть, или лабиринт, если какая- либо точка, движущаяся по линиям этой сети, может прийти к любой другой точке, не покидая линий нашей системы (или сети).
Приняв это может последовательно описать все линии сети без всяких скачков и перерывов и при этом по каждой линии сети она пройдет ровно два раза. При этом она, конечно же пройдет через точку обозначающую выход из лабиринта.
Возможность обхода следует, вообще говоря, из того, что фигуру, полученную
из сети двоением всех линий, можно описать одним росчерком.
Геометрическая сеть.
Слайд 11Правило 1. Отправляемся от выбранной вершины (первого перекрестка) и идем по любому ребру,
Правило 1. Отправляемся от выбранной вершины (первого перекрестка) и идем по любому ребру,
Тогда:
Если окажется, что мы попали в тупик, возвращаемся назад и пройденное ребро должно быть уже отброшено, так как мы прошли его два раза (туда и обратно).
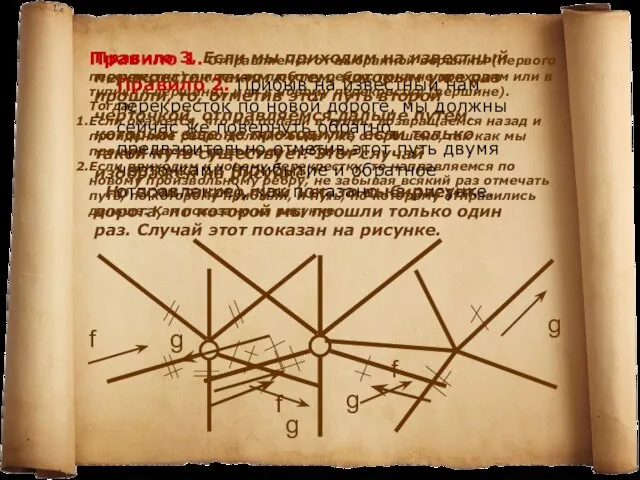
Если приходим к новому перекрестку, то направляемся по новому произвольному ребру, не забывая всякий раз отмечать путь, по которому прибыли, и путь, по которому отправились дальше. Как показано на рисунке.
f
g
Правило 2. Прибыв на известный нам перекресток по новой дороге, мы должны сейчас же повернуть обратно, предварительно отметив этот путь двумя черточками (прибытие и обратное отправление), как показано на рисунке.
f
g
Правило 3. Если мы приходим на известный перекресток таким путем, которым уже раз прошли, то, отметив этот путь второй черточкой, отправляемся дальше путем, которым еще не проходили, если только такой путь существует. Этот случай изображен на рисунке.
Но если такого пути нет, то выбирается дорога, по которой мы прошли только один раз. Случай этот показан на рисунке.
g
g
f
f
Слайд 12замечания:
Выходя из точки отправления, скажем А, мы ставим начальный знак (поперечную черточку).
Прохождение
замечания:
Выходя из точки отправления, скажем А, мы ставим начальный знак (поперечную черточку).
Прохождение

В любой момент прохождения, лабиринта, перед прибытием на какой-либо перекресток или после отправления из него, начальный перекресток (пункт отправления) имеет нечетное число знаков (черточек), а всякий другой перекресток имеет их четное число.
В любой момент, до или после прохода через перекресток, начальный перекресток имеет только один путь, обозначенный только одной черточкой. Всякий же иной из посещенных
уже перекрестков может иметь только два пути, обозначенных одной черточкой.
5. После полного обхода лабиринта у всех перекрестков все пути должны иметь по две черточки» Это, впрочем, входит прямо в условие задания.
1. Головоломный лабиринт
Приведем один не построенный, а только начерченный лабиринт (рис. 1
с готовым и упрощенным решением его: все тупики (слепые проходы) в нем уже заштрихованы, и главнейшие пути указаны точечными или штриховыми линиям. И по решению, данному на этой фигуре, видно, что от А надо сначала идти к С и потом от F к В, но, когда мы придем к С, у нас появляются три дороги, обозначенные 1, 2, 3, чтобы, дойти до D, Точно так же, когда мы дойдем до Е, тоже видны три дороги, обозначенные 4, 5, 6, чтобы дойти до F. У нас есть также обозначенная точками дорога от С до Е, другая—обозначенная точками дорога от D до F и проход от D до Е, указанный звездами. Мы можем, следовательно, выразить положение дела маленькой упрощенной диаграммой на рис. 2.
Здесь , все пути соответствуют путям кругообразного лабиринта, но только более доступны глазу.
A
C
D
E
F
B
рис. 2
Слайд 13 2. Беседка
А теперь, для вас будет нетрудно найти путь к беседке,
2. Беседка
А теперь, для вас будет нетрудно найти путь к беседке,

3. Еще лабиринт
Вот ещё любопытный образчик лабиринта, в котором надо пробраться по кратчайшей дороге к центру рисунке.
 ДЦП
ДЦП  Презентация на тему Лишайники, водоросли, мхи
Презентация на тему Лишайники, водоросли, мхи Тактика поведения в сложных ситуациях взаимодействия
Тактика поведения в сложных ситуациях взаимодействия Драма как род литературы
Драма как род литературы Презентация на тему Раскрытие скобок
Презентация на тему Раскрытие скобок  RTV 133
RTV 133 Болезни зубов
Болезни зубов Развитие орфографической зоркости у младших школьников
Развитие орфографической зоркости у младших школьников Презентация на тему Синергетика
Презентация на тему Синергетика  Черное и белое духовенство
Черное и белое духовенство Теории происхождения права
Теории происхождения права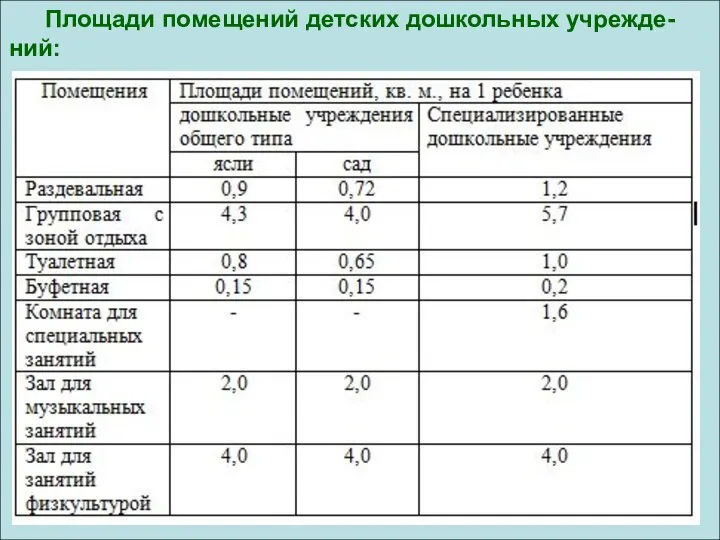 Площади помещений детских дошкольных учреждений
Площади помещений детских дошкольных учреждений Характеристика перцептивной стороны общения
Характеристика перцептивной стороны общения 1-й квест
1-й квест Курс CMS Wordpress. Практика. Выбор тематики своего сайта
Курс CMS Wordpress. Практика. Выбор тематики своего сайта Подростковые и молодежные субкультуры XXI века
Подростковые и молодежные субкультуры XXI века Мини-музей "Югра"
Мини-музей "Югра" Исследовательская краеведческая работа ученика 11 «А» класса Андреевской СОШ Судогодского района Владимирской области Воронин
Исследовательская краеведческая работа ученика 11 «А» класса Андреевской СОШ Судогодского района Владимирской области Воронин Методика Масару Ибука
Методика Масару Ибука Структура современного урока. Роль мотивации и рефлексии в учебном процессе
Структура современного урока. Роль мотивации и рефлексии в учебном процессе Как оформить инвестиции: от простого к сложному
Как оформить инвестиции: от простого к сложному Использование национально-регионального компонента в обучении химии на элективных курсах
Использование национально-регионального компонента в обучении химии на элективных курсах Дистанция в заданном направлении
Дистанция в заданном направлении Животные долгожители
Животные долгожители Здравствуй, Зимушка-Зима!
Здравствуй, Зимушка-Зима! Методы генной инженерии
Методы генной инженерии ВИРТУАЛЬНАЯ ЛЕКСИКОГРАФИЧЕСКАЯ ЛАБОРАТОРИЯ ДЛЯ ТОЛКОВЫХ СЛОВАРЕЙ VIRTUAL LEXICOGRAPHICAL LABORATORY FOR EXPLANATORY DICTIONARIES Остапова И. В. (
ВИРТУАЛЬНАЯ ЛЕКСИКОГРАФИЧЕСКАЯ ЛАБОРАТОРИЯ ДЛЯ ТОЛКОВЫХ СЛОВАРЕЙ VIRTUAL LEXICOGRAPHICAL LABORATORY FOR EXPLANATORY DICTIONARIES Остапова И. В. ( Технология проблемного обучения на уроках русского языка
Технология проблемного обучения на уроках русского языка